Venn Diagrams and Set Notation

A Venn Diagram is a way to visualize set relations between a finite number of sets. Below is a Venn Diagram for three sets $T, D,$ and $H$ .

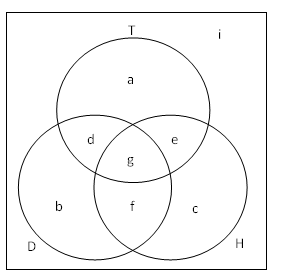Venn Diagram Sets

We introduce some notation from Set Theory:

$|T|$ is the number of elements in set $T$ .

Intersection of two sets, denoted $\cap$ , refers to the elements that are in both sets. In the example, $T \cap D = \{ d, g\}$ .

Union of two sets, denoted $\cup$ , refers to the elements that are in at least one of the two sets. In the example, $T \cup H = \{a, c, d, e, f, g\}$ .

Complement (Absolute), denoted $^c$ , refers to the elements that are not in the set. In the example, $D^c = \{ a, c, e, i\}$ .

Complement (Relative), denoted $\backslash$ , refers to the elements in the first set, but are not in the second set. In the example, $H\backslash T = \{ c, f \}$ .

Symmetric Difference, denoted $\triangle$ , refers to the elements that are in at least one of the two sets, but are not in both sets. In the example, $D \triangle H = \{b, c, d, e\}$ .

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Venn Diagrams and Set Notation

We introduce some notation from Set Theory:

Comments