Voltages in Capacitor Network

Here is an interesting problem recently shared by Neeraj.

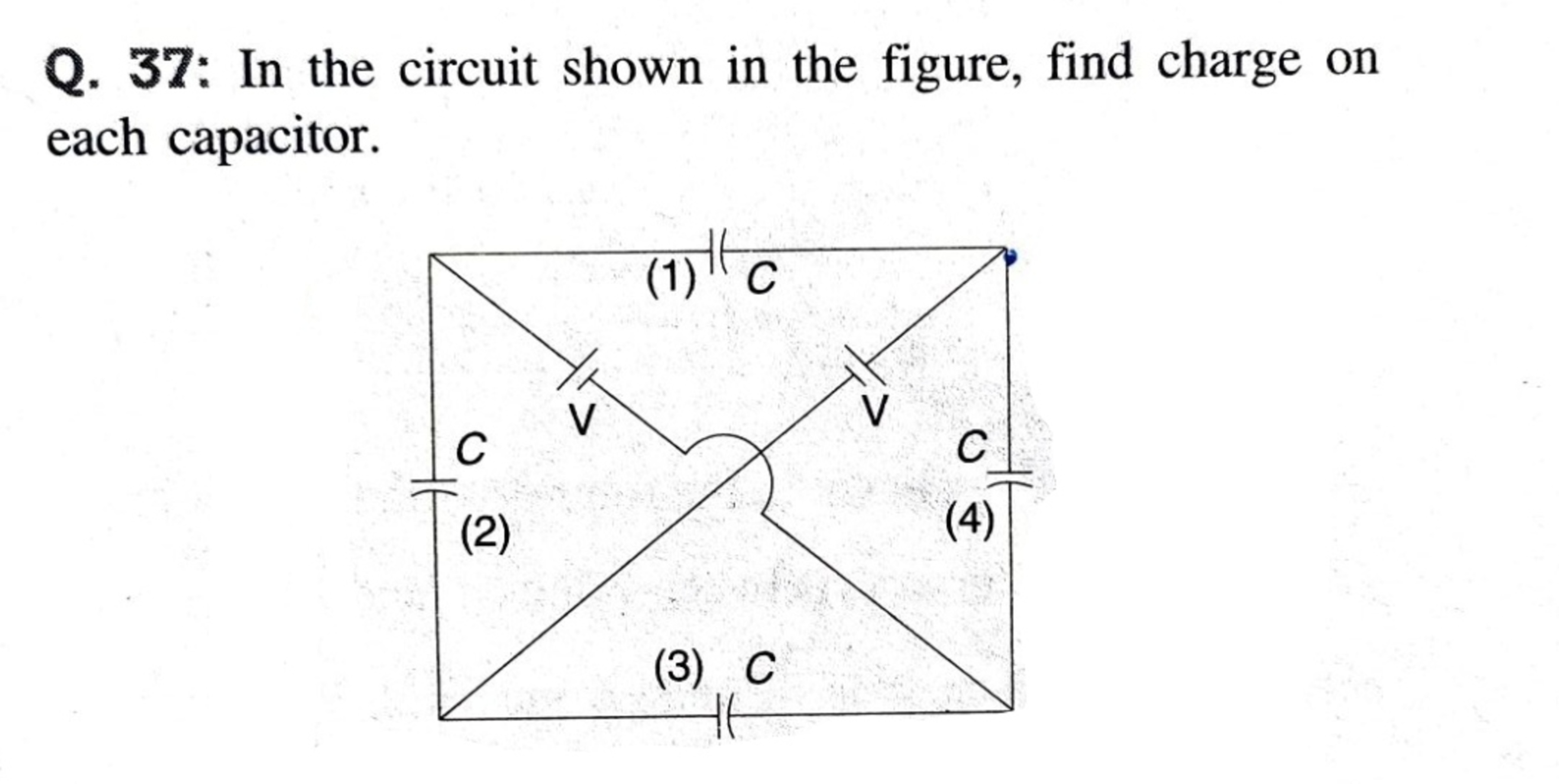
As far as I can tell, there are infinitely many solutions, because when you write a system of four linear equations, the system matrix always ends up being singular. Let $V_1, V_2, V_3, V_4$ be the capacitor voltages. To get a solution, declare the value of $V_1$ and solve a system of three linear equations to get the other three voltages. The system of three linear equations is non-singular.

The following equations describe the system (being mindful of the capacitor polarities):

$V_2 - V_1 - V_4 + V_3 = 0 \\ V_2 + V_3 = V \\ V_4 - V_3 = V$

Since we are declaring the value of $V_1$ , move it over to the other side:

$V_2 - V_4 + V_3 = V_1 \\ V_2 + V_3 = V \\ V_4 - V_3 = V$

Recall that $V$ is the battery voltage. For $V_1 = 0$ , $(V_2, V_3, V_4) = (V,0,V)$ . For $V_1 = 2V$ , $(V_2, V_3, V_4) = (3 V,-2 V,-V)$ . These are just two solutions out of infinitely many possibilities.

One other thing to note. The following relation also holds:

$V + V_1 - V + V_3 = 0 \\ V_1 + V_3 = 0$

So if $V_1$ is chosen as a positive value, $V_3$ will be negative. If one wishes to impose an additional constraint that none of the capacitor voltages can be negative, it follows that $V_1$ and $V_3$ are both zero.

Markdown

Appears as

*italics* or _italics_

italics

**bold** or __bold__

bold


- bulleted
- list

bulleted
list


1. numbered
2. list

numbered
list

Note: you must add a full line of space before and after lists for them to show up correctly

paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)

example link

> This is a quote

This is a quote

    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"

# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"

Math

Appears as

Remember to wrap math in $ ... $ or \[ ... \] to ensure proper formatting.

2 \times 3

2 \times 3

2^{34}

2^{34}

a_{i-1}

a_{i-1}

\frac{2}{3}

\frac{2}{3}

\sqrt{2}

\sqrt{2}

\sum_{i=1}^3

\sum_{i=1}^3

\sin \theta

\sin \theta

\boxed{123}

\boxed{123}

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

@Lil Doug

Notice how the $V_1 = 0$ case corresponds to the expected solution.

Steven Chase - 10 months, 1 week ago

The final comment that I just added seems relevant also. Perhaps the question assumes that all capacitor voltages must be positive, in which case their solution is indeed the only allowable one.

@Steven Chase how do you know the polarities of capacitor?

Talulah Riley - 10 months, 1 week ago

The curved side is negative, and the flat side is positive

@Steven Chase now I am little bit more confused in this probelm.
Why we are doing $V_{1}=0$

If all capacitor voltages must be positive (or at least not negative), $V_1$ has to be zero. See the last part of the note. Otherwise, it is just an arbitrary choice, given that the general four by four system is singular.

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$