Wanted help in these

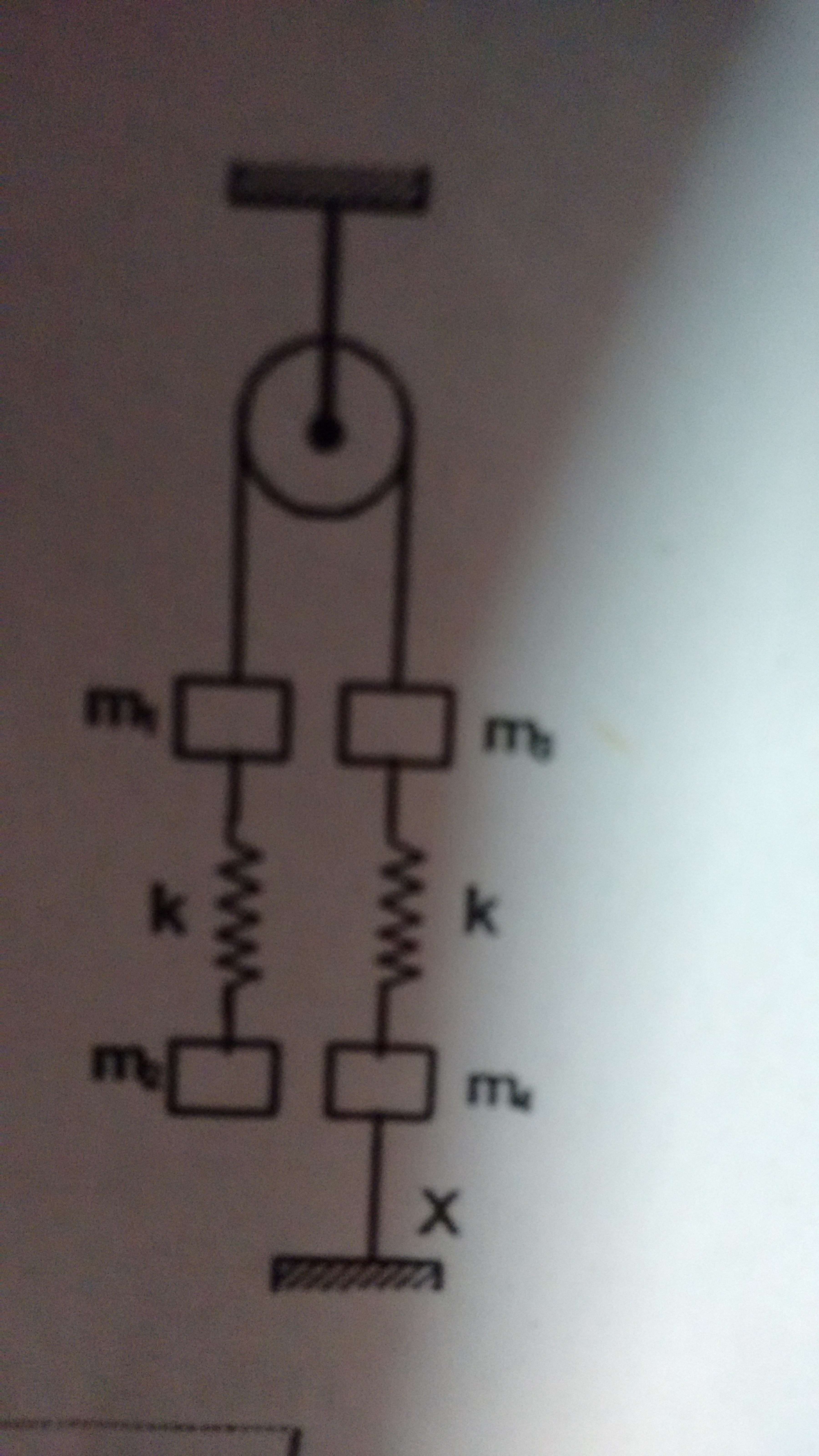
1) For the system shown in the figure the acceleration of the mass $m_{4}$ immediately after the lower thread $x$ is cut will be (assume the threads and springs are light and there is no friction) The diagram is above mass $m_{4}$ is with string and above it is $m_{3}$ towards left of $m_{3}$ is $m_{1}$ .

2) If $f(x)$ is an increasing function and $\large{\displaystyle \int_{0}^{x} 2xf^{2}(t).dt=(\displaystyle \int_{0}^{x} 2f(x-t).dt)^{2}}$ for $f(1)=1$ and $f(x)$ is continuous for $x>0$ . Find $f(x)$

3) Let $f(x)=sin^{4} \pi x$ and $g(x)=lnx$ . Find the whole area bounded by $y=f(x)$ and $y=g(x)$ and $x=0$

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Nice problems.

Just write free body diagrams for each block. What you need to find is the force in the right hand side spring. Once the string is cut, the force in the right hand side spring is the only thing other than gravity acting on $m_4$ . After solving using F.B.D, you will get the force.
Firstly, substitute $x-t$ in place of $t$ in the RHS integral. Then take derivative w.r.t $x$ on both sides. Use the given equation and substitute RHS in place of LHS wherever necessary after taking derivative. If done right, you will now be having an equation in which you have $\int _{ 0 }^{ x }{ f\left( x \right) dx }$ , $f(x)$ and $x$ only. You can now write this as a differential equation where $y=\int _{ 0 }^{ x }{ f\left( x \right) dx }$ . Since the differential equation is of 2nd degree, you will have to use quadratic formula. Finally, after solving, you will get two solutions, but only one of them satisfies all conditions given in problem.
$f(x)$ and $g(x)$ intersect only once and that is at $x=1$ . Hence the required answer is $\int _{ 0 }^{ 1 }{( \sin ^{ 4 }{ \pi x } +\log { x }) }dx = \frac{11}{8}$

@Tanishq Varshney

Raghav Vaidyanathan - 6 years, 1 month ago

but in the 3) they have five solutions. why we took only $0$ to $1$

Tanishq Varshney - 6 years, 1 month ago

That is correct, but there the areas are not also bounded by $x=0$ .

Raghav Vaidyanathan - 6 years, 1 month ago

@Raghav Vaidyanathan – ok, now i understood, can u please elaborate 2) one

Tanishq Varshney - 6 years, 1 month ago

Hi Raghav! Could you please help me here

satvik pandey - 6 years, 1 month ago

Answers i have are 1) $[\frac{m_{3}+m_{4}-m_{1}-m_{2}}{m_{4}}]g$ $\quad$ 2) $f(x)=x^{\sqrt{2}+1}$ $\quad$ 3) $\frac{11}{8}$

Tanishq Varshney - 6 years, 1 month ago

Let the tension in the above string be $T$ . And let the extension of left and right springs be $x$ and $x_{2}$ .

From the free body diagrams we get

$T=m_{1}g+kx$ .....................(1)

$kx=m_{2}g$ ...............................(2)

$m_{3}g+kx_{2}=T$ ............................(3)

From 1 and 2 we get $T=(m_{1}+m_{2})g$

From (2)

$kx_{2}=(m_{1}+m_{2}-m_{3})g$

Now when the lower string is cut then only gravitational force and force spring due to string will act on it.

Let the acceleration of $m_{4}$ be $a$ be in downward direction---

So $m_{4}g-kx_{2}=m_{4}a$

So $a=\frac { g(m_{ 4 }+m_{ 3 }-m_{ 1 }-m_{ 2 }) }{ m_{ 4 } }$

satvik pandey - 6 years, 1 month ago

Thanx for the solution $\ddot \smile$

Tanishq Varshney - 6 years, 1 month ago

@Tanishq Varshney – You are welcome!! :)

satvik pandey - 6 years, 1 month ago

You can solved it orally , by using the newton's 2nd law , directly : Since Tension's is internal forces ...

${ F }_{ ext }=ma$

system is moving with same acceleration , ideal strings , inextinsible , so
${ F }_{ ext }=ma\\ { m }_{ 3 }g+{ m }_{ 4 }g-{ m }_{ 1 }g-{ m }_{ 2 }g={ m }_{ 4 }a$

hence the answer....

ankit kumar - 6 years, 1 month ago

@Raghav Vaidyanathan @satvik pandey @Nishant Rai @rachit parikh

Tanishq Varshney - 6 years, 1 month ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$