Water Clock Problem

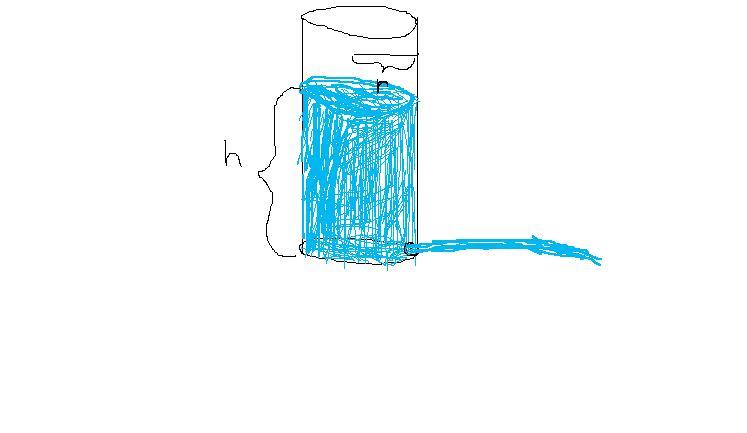
Given a cylinder filled to a height h with water how long will it take to empty though a small hole of area A.

#Physics #Advice #Opinions

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

WE ARE HERE INTERESTED IN FINDING THE TIME REQUIRED TO EMPTY A TANK,IF A HOLE IS MADE AT THE BOTTOM OF THE TANK..........::::::::: you have given that tank is filled with water....so the density of water is 1 gm/cc.......we would take this during our calculation.......ok………...now think that the cross sectional area of the hole is "a"........... area of the cross section of the tank is surely pi(r^2)=A (let us consider)........let at some instant of the time the level of liquid in the tank is “y”……..velocity of efflux at this instant of time would be……..v=sqrt(2gy)…………:::::::::: now , at this instant volume of liquid coming out of the hole per second is (dV/dt)=av…………..volume of liquid coming down in the tank per second is also (dV/dt)=A(-dy/dt)……….i think you have understood till now…………. Now, av =A(-dy/dt)………..asqrt(2gy)=A(-dy/dt)……….now integrate both sides taking same quantities in the same side….you would get…….integration [0 to t] dt= (-A/{asqrt(2g)})* integration[H to 0] y^(-.5) dy…...…………….so we get,........... t=(A/a)sqrt(2H/g) where A=pir^2....(as you gave)……:)(:……..PLEASE LET ME KNOW IF ANYTHING IS WRONG……..:|*

Sayan Chaudhuri - 8 years, 1 month ago

Ya that's how it's derived. I was a bit lazy(I gave the answer late night) so just gave the answer without the derivation :P

Saurabh Dubey - 8 years, 1 month ago

That seems like the right answer using physical considerations.

Samuel Queen - 8 years, 1 month ago

I'am assuming that the area of cross section of the cylinder is A1 and A<<<<A1. Then the answer should be $\frac {A1}{A} \times \sqrt{\frac{2h}{g}}$

Saurabh Dubey - 8 years, 1 month ago

This is a hydraulics problem in orifice.To determine the time to empty the tank.Use Bernoulli's theorem v1^2/2g+p1/y+h1=v2^2+p2/y+h2.Since the container is open.The pressure is zero and to the nozzle because of atmospheric pressure.Where h1=h and h2=0 reference to the datum of orifice.neglect the velocity in v1 ,it will not effect your computation because v1 are to small velocity.You will get h=v1^2/2g equation 1.The discharges of water in the orifice looks like a projectile.It will occupy range or distance from the orifice .V1=X/t equation 2.substitute equation 1 to 2 then you will get the time to empty the tank.This is theoretical not including the head loss.

EDSEL SALARIOSA - 8 years, 1 month ago

It is probably going to involve integrals. What have you tried so far?

Pranav Arora - 8 years, 1 month ago

assuming the upper height be 'h' and lower height be 'H-h' time = 2(H-h)/g whole under root

Mudit Tripathi - 8 years, 1 month ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$