What about these

Q1) If $cos(x-y)+cos(y-z)+cos(z-x)=\frac{-3}{2}$ and $cosx+cosy+cosz=a$ and $sinx+siny+sinz=b$ . Find $a$ and $b$

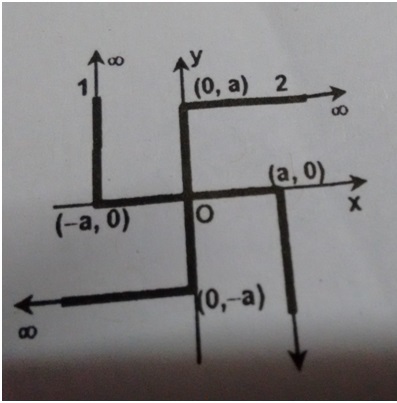
Q2) Two non-conducting infinite wires have shapes as shown above. The linear charge densities of wire (1) and wire (2) are

$x\quad if\quad x\leq -a~ and~ x\geq a\\ \\ 0\quad if\quad -a<x<a)$

and

$y\quad if\quad y\leq -a~ and~ y\geq a\\ \\ 0\quad if\quad -a<y<a)$

respectively where $(x,y)$ are coordinates of points on the wire. An electron is released from origin, the unit vector along the direction of velocity of the electron just after its release will be in terms of $\hat { i }$ and $\hat { j }$

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

$cosx + cosy + cosz = a$

$\cos^2x + \cos^2y + \cos^2z + 2\cos x\cos y + 2\cos y\cos z + 2 \cos x\cos y = a^2$

Likewise, $\sin^2x + \sin^2y + \sin^2z + 2\sin x\sin y + 2\sin y\sin z + 2 \sin x\sin y = b^2$

Adding, $\cos^2x + \cos^2y + \cos^2z + 2\cos x\cos y + 2\cos y\cos z + 2 \cos x\cos y +$

$\sin^2x + \sin^2y + \sin^2z + 2\sin x\sin y + 2\sin y\sin z + 2 \sin x\sin y = a^2 + b^2$

$\implies 1 + 1 + 1 + 2(\cos x\cos y + \cos y\cos z + \cos x\cos y + \sin x\sin y + \sin y\sin z + \sin x\sin y) = a^2 + b^2$

$\implies 3 + 2(\cos(x-y) + \cos(y-z) + \cos(z-x)) = a^2 + b^2$

$\implies 3 + 2* \frac{-3}{2} = a^2 + b^2$

$0 = a^2 + b^2 \implies a = 0\quad \& \quad b = 0$

Siddhartha Srivastava - 6 years, 1 month ago

Thanks for this man.

Raghav Vaidyanathan - 6 years, 1 month ago

@Raghav Vaidyanathan @Ronak Agarwal @Mvs Saketh

Tanishq Varshney - 6 years, 1 month ago

The answer to q 1 is very easy: $a=b=0$ .

Raghav Vaidyanathan - 6 years, 1 month ago

Ans 2 q2 seems to be zero too.

Raghav Vaidyanathan - 6 years, 1 month ago

can u explain in brief the first part

Tanishq Varshney - 6 years, 1 month ago

@Tanishq Varshney – for first one The simplest way is to assume all the three angle differences equal, which ofcourse then must be 120 degree, so just consider 1 , w ,w^2 , add em up

Mvs Saketh - 6 years, 1 month ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$