What is Going on Here? Would like an answer, please!

So I was trying to derive a way to approximate $\pi$ using my compass and straightedge, and then use algebra. I began by creating a $30$ degree angle:

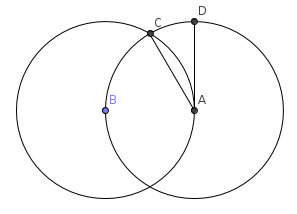
So $CAD$ is $30$ degrees. Then, I imagined bisecting this angle into infinity. Notice if we draw a segment from $C$ to $D$ , we get an isosceles. We can calculate for this length using the law of cosines: $x = \sqrt{2-2\cos(\frac{30}{2r}})$ , where $r$ is a reiteration (another bisection). So, if I am correct in my assumption, $\pi$ should be about $x \cdot n$ , if $n$ are the number of divisions in the circle. We can find $n$ easily enough: $n = 24 \cdot 2^{r-2}$ . we know this becuase, as we bisect, we get a table of values: $\left \{ 24, 48, 96, \ldots \right \}$ . Likewise, we find $\theta$ thusly: $\theta = \frac{30}{2^{r}}$ . This table of values is found by dividing 360 by $n$ : $\left \{ 30, 15, 7.5, ... \right \}$ . So to find $x$ , we use the law of cosine, take the square, and multiply by n. This gives me the equation: $\pi = \sqrt{2- 2 \cdot \cos \dfrac{30}{2^{r}}} \cdot 24 \cdot 2^{r-2}$ This makes sense from the way I constructed it, but not here: $\lim_{r \rightarrow \infty} \sqrt{2- 2 \cdot \cos \frac{30}{2^{r}}} \cdot 24 \cdot 2^{r-2}$

This becomes: $\lim_{r \rightarrow \infty} \sqrt{2- 2 \cdot \cos(30 \cdot 0)} \cdot 24 \cdot 2^{r-2} = 0$ Obviously, $\pi \neq 0$ . So, I tested with two values of $r$ that my calculator could handle. For $r =17$ , $\pi = 3.14159265358$ (correct to 11 decimal places.) However, at $r = 18$ , $\pi = 3.1415$ (correct to only 4 decimal places.) So why does this equation get close to $\pi$ , as it is supposed to, and then stop, and then appear to approach zero? Thanks for the help, I am not all that great at math, and would really appreciate it!

Markdown

Appears as

*italics* or _italics_

italics

**bold** or __bold__

bold


- bulleted
- list

bulleted
list


1. numbered
2. list

numbered
list

Note: you must add a full line of space before and after lists for them to show up correctly

paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)

example link

> This is a quote

This is a quote

    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"

# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"

Math

Appears as

Remember to wrap math in $ ... $ or \[ ... \] to ensure proper formatting.

2 \times 3

2 \times 3

2^{34}

2^{34}

a_{i-1}

a_{i-1}

\frac{2}{3}

\frac{2}{3}

\sqrt{2}

\sqrt{2}

\sum_{i=1}^3

\sum_{i=1}^3

\sin \theta

\sin \theta

\boxed{123}

\boxed{123}

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Extremely interesting! How are you saying that limit is 0? (Hint: It's an indeterminate form, ( $0 \cdot \infty$ ))
The correct limit is $\pi$ , just like you wanted.

Ameya Daigavane - 5 years, 2 months ago

Well, it seemed like as r approached infinity, the cosine would approach 0. of course, cos(0) = 1 and so we would get $0 * 24 * 2^{r-2}$ . Since the limit is $\pi$ , is there something wrong with my calculations? Since the precision seemed to degrade for higher r's. Thanks, I don't have the experience of ever learning limits in school, so I do not realize there is such a thing as indeterminate forms, but I was unsure what to do with the $0 * \infty$ case. I just assumed for any number, you would get zero. Thanks for the help! :)

Drex Beckman - 5 years, 2 months ago

Oh okay, I'll try to explain then. Suppose you had two functions, $f(x)$ and $g(x)$ ,
$\lim_{x \to \infty} f(x) = \infty$ and $\lim_{x \to \infty} g(x) = 0$ . Now what is $\lim_{x \to \infty} f(x)\cdot g(x)$ ?

If you think about it, you really can't say, because it could be $0$ or $\infty$ or some value in between.
Why? It depends on the functions $f(x)$ and $g(x)$ themselves.
Let me give you some examples. Let $L = \lim_{x \to \infty} f(x)\cdot g(x)$ .

$f(x) = x$ and $g(x) = \frac{1}{x} \Rightarrow L = 1$ as $f(x)g(x) = 1$ always.
$f(x) = x^2$ and $g(x) = \frac{1}{x} \Rightarrow L = \infty$ as $f(x)g(x) = x$ always.
$f(x) = x$ and $g(x) = \frac{1}{x^2} \Rightarrow L = 0$ as $f(x)g(x) = \frac{1}{x}$ always.
$f(x) = 5x$ and $g(x) = \frac{1}{x} \Rightarrow L = 5$ as $f(x)g(x) = 5$ always.

So, we've seen that the limit can be anything really. This is why we call $0 \cdot \infty$ an indeterminate form, it can 'evaluate' to anything.

Now, to your question, how do we evaluate $\lim_{r \rightarrow \infty} \sqrt{2- 2 \cdot \cos \frac{30}{2^{r}}} \cdot 24 \cdot 2^{r-2}$ ?
Here, $f(x) = 24 \cdot 2^{r - 2}$ and $g(x) = \sqrt{2 - 2 \cdot \cos \frac{30}{2^r}}$ (Understand why.)
So what is L, here?
(Convert $30$ to $\frac{\pi}{6}$ radians)
L = $\lim_{r \rightarrow \infty} \sqrt{2- 2 \cdot \cos \frac{\pi}{6 \cdot 2^{r}}} \cdot 6 \cdot 2^{r}$
Let $t = \dfrac{1}{6\cdot 2^r}$ .
L = $\lim_{t \rightarrow 0} \dfrac{\sqrt{2- 2 \cdot \cos \pi t }}{t} = \lim_{t \rightarrow 0} \dfrac{\sqrt{2}\sqrt{1 - \cos \pi t }}{t} = \lim_{t \rightarrow 0} \dfrac{\sqrt{2}\sqrt{2 \sin^2 \frac{\pi t}{2}}}{t} = \lim_{t \rightarrow 0} \dfrac{2 sin \frac{\pi t}{2}}{t} = \pi$

I used the well-known facts that $1 - \cos 2x = 2 \sin^2 x$ and $\lim_{x \to 0} \frac{\sin x}{x} = 1$ .

@Ameya Daigavane – Well explained.

It's a very common misconception to "Let $n \rightarrow \infty$ in a specific portion of the expression, while ignoring the rest of it".

Calvin Lin Staff - 5 years, 2 months ago

@Ameya Daigavane – Thanks a lot, I think I understand it now! Very clear explanation, also! +1

@Drex Beckman – Thanks! Also, the reason your calculator drops off in precision is because of rounding off errors and approximate values for the cosines and sines.

@Ameya Daigavane – Right, that was what I suspected, but I put a bit too much faith in the arbitrary precision calculations, I guess. xD

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$