What is the general term of this sequence?

I have long been fascinated with sequences, may it be an arithmetic sequence, a geometric sequence, or a general sequence. After a week, I have thought of a sequence where the terms are the number of points in cubes (except for the first term where it is a point). In each consecutive term, the number of points on each edge of the previous cube increases by $1$ .

I have attempted to solve for the $n^{th}$ term of this sequence I have thought of more than $2$ months ago, but unfortunately even after many attempts and many methods, I have failed.

Can anyone solve for the general term of $1, 8, 20, 32, 44, 56, 68, 80, 92, 128, \ldots$ ? Is it possible to do so, or does it not have a general term?"

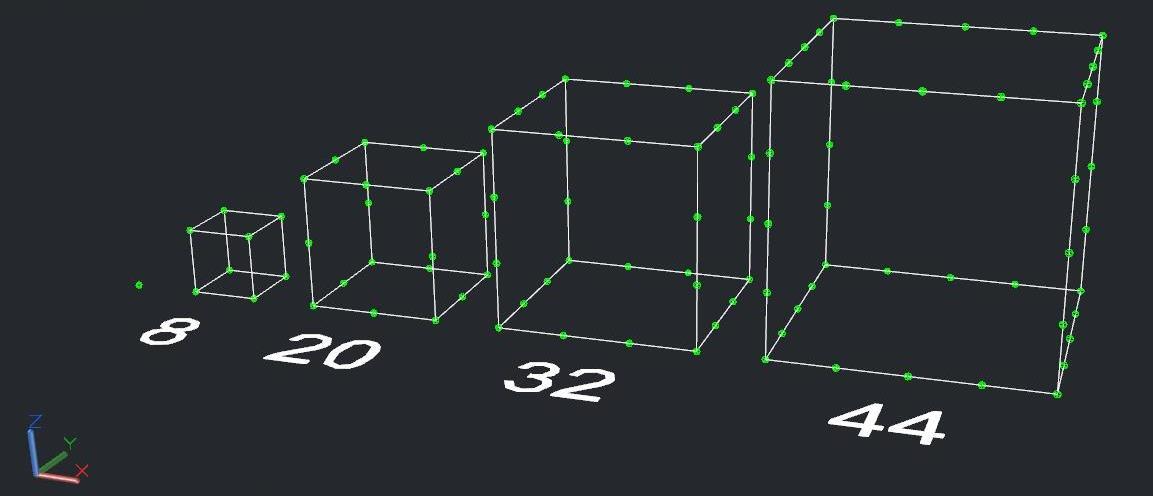
Note: This view is in perspective.

#Algebra #Sequences #Cubes #Cube #sequence

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

The only hiccup is the first term $1$ . Otherwise, if we dropped that and went with $8, 20, 32, 44...$ , the series formula $12n-4$ will do. That might be why you're having so much trouble.

If it's really important to include that first term $1$ , it's still possible but won't be so simple.

Edit: Okay, here it is. This will generate your series, for $n=1,2,3,4,5,6...$ it delivers $1,8,20,32,44,56...$

$f\left( n \right) =\dfrac { 5 }{ 2 } \left(1-{ \left( -1 \right) }^{ { 2 }^{ n-1 } }\right)+12n-16$

I told you it wouldn't be simple.

Michael Mendrin - 5 years, 8 months ago

I see that substituting $1$ for $n$ in that function will also result in $1$ . Unfortunately, it does not work for greater positive integers. However, I have noticed that substituting $2$ , $3$ , $4$ , $5$ , $6$ , $7$ , $8$ , $9$ and $10$ for $n$ in the function $f(n) = 12n - 16$ will give the right value for $f(n)$ , respectively.

Adriel Padernal - 5 years, 8 months ago

The difference between successive terms should be 12, starting with the 2nd and 3rd terms. The only counterexample to that is between the 1st and 2nd term. The formula I have is quite correct, it works.

Michael Mendrin - 5 years, 8 months ago

@Michael Mendrin – I stand corrected, I apologize for my error. I must not have carefully foreseen and analyzed the formula you have given for the general term. Thank you very much, this means a lot to me. Again, my apologies.

Adriel Padernal - 5 years, 7 months ago

May I ask, how did you get this formula?

Adriel Padernal - 4 years, 11 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$