Why do we neglect the negative root?

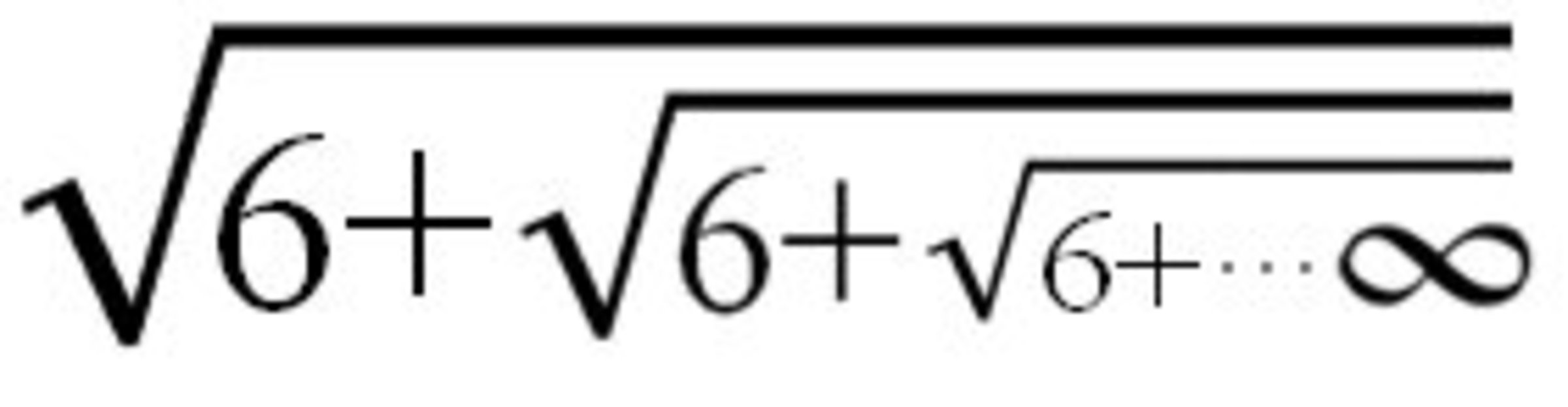
Let \sqrt{6}+\sqrt{6}+\sqrt{6}...∞ = x

So, x = \sqrt{6} + x

x^{2} = 6 + x

So, we have got a quadratic equation and we can solve it to get x = 3 and -2. We write x = -2 is not possible. So, x = 3. But, why is this so?Why is x = -2 is not possible?

The square root of any number can be both positive and negative, and x is in the form of a square root so the root can also be -2.So, why do we neglect x = -2 ?

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Yeah, we solve this by squaring, but remember that squaring an equation can yield other, unwanted solutions that have to be checked against the original problem to ensure that they make sense.

In this case, it's what Nishant said: the radical symbol denotes only the positive square root of an expression, by definition. So the negative root of the squared equation does not make sense in the original context.

Think of it as multiplying a given equation on both sides to eliminate a denominator of (x -1) and getting x = 1 as a root. Will that be a valid solution?

Raj Magesh - 7 years, 7 months ago

I think the square root we usually talk about refers to the principal square root which is always positive.

Nishant Sharma - 7 years, 7 months ago

Actually, -2 is an extraneous solution.

Satvik Golechha - 7 years, 3 months ago

But how do we confirm that -2 is an extraneous solution. By putting it in the original equation, we again get -2 and this continues.

Prakkash Manohar - 7 years, 3 months ago

we can check it by putting,when we put -2,we get again 2 0r -2 as possible values of x,but 2 is not the solution of x.

Aditya Kumar - 7 years, 3 months ago

I might be wrong.. but i think that you have been misinformed .. cause whenever I do these kind of questions there is always both the solutions in the options of MCQ..!! I have this exact same ques in a book and the given options are: A) 3,-2 B)3,2 C)-3,-2 D) None of the above and the correct option in the answers was 'A' itself!

Arpit Shukla - 7 years, 3 months ago

I want to ask that why do we take x = √ 6 + x ??

Ayush Porwal - 7 years, 2 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$