In the previous note that I've written I said sinx=1!x−3!x3+5!x5−7!x7+⋯
This can come in handy today!
We know the function image of sinx is:
 First we can say sinx≈(π+x)x(π−x) because when x=−π or 0 or π the (π+x)x(π−x)=0 and sinx=0. But let we see the function image (the blue line):
First we can say sinx≈(π+x)x(π−x) because when x=−π or 0 or π the (π+x)x(π−x)=0 and sinx=0. But let we see the function image (the blue line):
 This fits too badly! (sinx)′=cosx and when x=0 then (sinx)′=1. Can we let [C1×(π+x)x(π−x)]′=1 when x=0?
Let [C1×(π+x)x(π−x)]′=1 which C1 is a constant. So
C1×[(π+x)x(π−x)]′=1 when x=0. After expansion, derivation, only "π2" is left, and the others are all 0 because they contain x (ie 0). So
C1×π2=1
C1=π21
π21(π+x)x(π−x)=(1+πx)x(1−πx)
Then it will become like this:
This fits too badly! (sinx)′=cosx and when x=0 then (sinx)′=1. Can we let [C1×(π+x)x(π−x)]′=1 when x=0?
Let [C1×(π+x)x(π−x)]′=1 which C1 is a constant. So
C1×[(π+x)x(π−x)]′=1 when x=0. After expansion, derivation, only "π2" is left, and the others are all 0 because they contain x (ie 0). So
C1×π2=1
C1=π21
π21(π+x)x(π−x)=(1+πx)x(1−πx)
Then it will become like this:
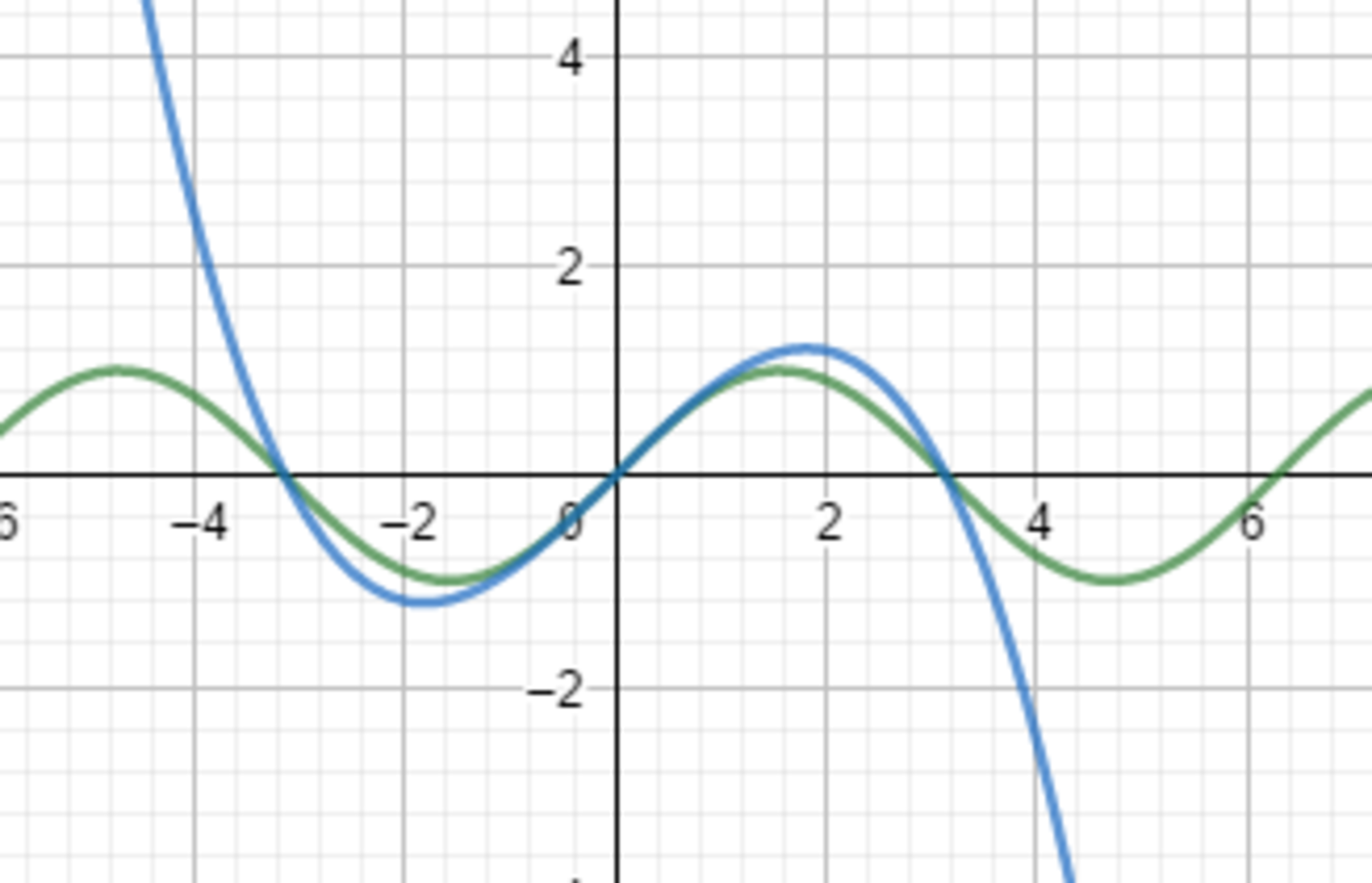 It's great! The same, sinx≈(2π+x)(1+πx)x(1−πx)(2π−x)
C2×[(2π+x)(1+πx)x(1−πx)(2π−x)]′=1
only "(2π)2" is left, and the others are all 0 because they contain x (ie 0). So
C2=(2π)21
(2π)21(2π+x)(1+πx)x(1−πx)(2π−x)=(1+2πx)(1+πx)x(1−πx)(1−(2π)2x)
And so on:
C3=(3π)21,C4=(4π)21,Cn=(nπ)21⋯
Therefore
sinx=⋯(1+2πx)(1+πx)x(1−πx)(1−(2π)2x)⋯
We also know (a+b)(a−b)=a2−b2. Then
sinx=x(1−π2x2)(1−(2π)2x2)(1−(3π)2x2)⋯
and sinx also is
1!x−3!x3+5!x5−7!x7+⋯
So
1!x−3!x3+5!x5−7!x7+⋯=x(1−π2x2)(1−(2π)2x2)(1−(3π)2x2)⋯
Therefore, the split items with x3 items on the left and right are equal.
In the left of the formula, it has −x33!1 and in the right of the formula -- how many x3 does it have?
We must have x3, remove the first x, it takes a ⋯x2 to form x3. So we have:
x3×(−3!1)=x(−π2x2−(2π)2x2−(3π)2x2−⋯)
3!1=π21+(2π)21+(3π)21+⋯
61=π21(121+221+(3π)21+⋯)
6π2=121+221+321+⋯
Proven!
It's great! The same, sinx≈(2π+x)(1+πx)x(1−πx)(2π−x)
C2×[(2π+x)(1+πx)x(1−πx)(2π−x)]′=1
only "(2π)2" is left, and the others are all 0 because they contain x (ie 0). So
C2=(2π)21
(2π)21(2π+x)(1+πx)x(1−πx)(2π−x)=(1+2πx)(1+πx)x(1−πx)(1−(2π)2x)
And so on:
C3=(3π)21,C4=(4π)21,Cn=(nπ)21⋯
Therefore
sinx=⋯(1+2πx)(1+πx)x(1−πx)(1−(2π)2x)⋯
We also know (a+b)(a−b)=a2−b2. Then
sinx=x(1−π2x2)(1−(2π)2x2)(1−(3π)2x2)⋯
and sinx also is
1!x−3!x3+5!x5−7!x7+⋯
So
1!x−3!x3+5!x5−7!x7+⋯=x(1−π2x2)(1−(2π)2x2)(1−(3π)2x2)⋯
Therefore, the split items with x3 items on the left and right are equal.
In the left of the formula, it has −x33!1 and in the right of the formula -- how many x3 does it have?
We must have x3, remove the first x, it takes a ⋯x2 to form x3. So we have:
x3×(−3!1)=x(−π2x2−(2π)2x2−(3π)2x2−⋯)
3!1=π21+(2π)21+(3π)21+⋯
61=π21(121+221+(3π)21+⋯)
6π2=121+221+321+⋯
Proven!
#Algebra
 First we can say because when or or the and . But let we see the function image (the blue line):
First we can say because when or or the and . But let we see the function image (the blue line):
 This fits too badly! and when then . Can we let when ?
Let which is a constant. So
when . After expansion, derivation, only "" is left, and the others are all 0 because they contain x (ie 0). So
Then it will become like this:
This fits too badly! and when then . Can we let when ?
Let which is a constant. So
when . After expansion, derivation, only "" is left, and the others are all 0 because they contain x (ie 0). So
Then it will become like this:
 It's great! The same,
only "" is left, and the others are all 0 because they contain x (ie 0). So
And so on:
Therefore
We also know . Then
and also is
So
Therefore, the split items with items on the left and right are equal.
In the left of the formula, it has and in the right of the formula -- how many does it have?
We must have , remove the first , it takes a to form . So we have:
Proven!
It's great! The same,
only "" is left, and the others are all 0 because they contain x (ie 0). So
And so on:
Therefore
We also know . Then
and also is
So
Therefore, the split items with items on the left and right are equal.
In the left of the formula, it has and in the right of the formula -- how many does it have?
We must have , remove the first , it takes a to form . So we have:
Proven!
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
Great! in this way you can also find the sum like ζ(4)=n=1∑∞n41=90π4 ζ(6)=n=1∑∞n61=945π6 ζ(8)=n=1∑∞n81=9450π8 ζ(10)=n=1∑∞n101=93555π10 For General ζ(2n)=2(2n)!(−1)n+1β2n(2π)2n Where βn= nth Bernoulli Number
Log in to reply
Great!