Xuming's Geometry Synthetic Group - Shivam's proposal
- The circumcircle of the quadrilateral has a radius 2. cut at such that . If . Find the area of quadrilateral .
- Triangle ABC is an isosceles triangle in which AB=A C. A circle is drawn passing through B and touching AC at its midpoint M. The circle cuts AB at P . Prove that BP=3AP.
- In an isosceles triangle the altitude drawn to the base is times the radius of the circumcircle . Prove the base angle of the triangle is .
- The sides of a right angled triangle are all integers . Two sides are prime that differ by 50.Find the smallest value of the third side.
- In triangle ABC , D is on BC such that BD=3DC. E is on AC such that 3AE=2EC. AD and BE cut F. Area of triangle AFE=4 and area of triangle BFD=30 . Find area of triangle ABC.
- In a circle AB is a diameter . AB is produced to P such that BP=Radius of the circle . PC is tangent to the circle . The tangent at B amd AC produced cut at E . Then describe triangle CDE.
No vote yet
1 vote
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
Q3:
Let the isosceles △ABC has AB=AC, its base angle be θ and the center and radius of the circumcircle be O and r respectively.
Then the extension of altitude AP to BC passes through O; AP=32r, OP=31r and then BP=OB2−OP2=r2−(31r)2=322.
Therefore, tanθ=BPAP=322r32r=21⇒cosθ=32⇒θ=cos−1(32)
Q5:
We note that △CFE has the same altitude as △AFE, therefore their areas are in the ratio of the base lengths. That is:
[△AFE][△CFE]=AEEC=23⇒[△CFE]=23×[△AFE]=23×4=6
Similarly, [△CFD]=BDDC×[△BFD]=31×30=10
And, [△ABD]=DCBD×[△ACD]=3×([△AFE]+[△CFE]+[△CFD])=3×(4+6+10)=60
Therefore, [△ABC]=[△ABD]+[△ACD]=60+20=80
Q:1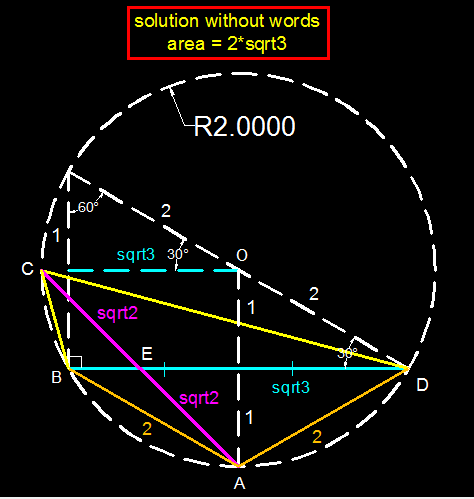
Q:2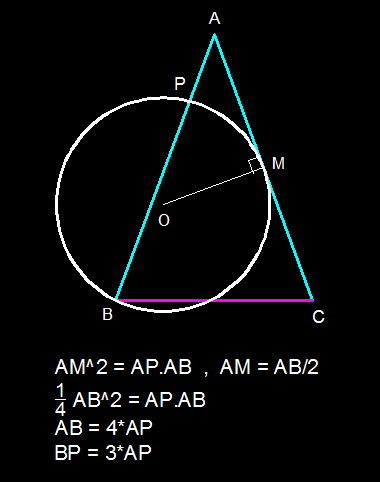
Answer 4 = 60