1, 2, 3 Tiling
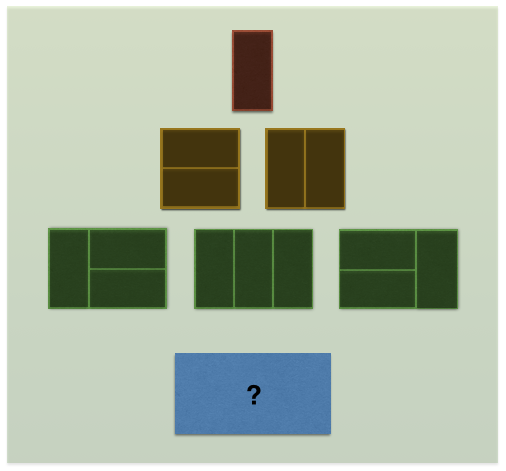Using 1'' x 2'' dominoes, there's one way to tile a 1'' x 2'' area, 2 ways to tile a 2'' x 2'' area, and 3 ways to tile a 3'' x 2'' area.
How many ways are there to tile a 4'' x 2'' area?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Almost. Just need to add another 1 to the beginning xD
Log in to reply
But theres only 1 way to tile a 0x2 space
Log in to reply
Not true. There are 0 ways to map that. Saying that there is a way (by not adding a domino) would alter all of the other sequences, as you would have to map no domino for each domino placed... Doubling the original answers. Nice idea, but the mathematics don't add up ;)
Log in to reply
@Jerith Jade – I think Steven may be on to something. For me it relates to the definition of factorial. I always had a hard time understanding why 0! was 1. But it was explained to me that you can think about factorial as the number of ways you can arrange that number of things in a group. So you can arrange 3 thinks 6 ways, 2 things 2 ways, 1 think 1 way and 0 things 1 way. Also when you look at the definition of tiling: "a way of arranging identical plane shapes so that they completely cover an area without overlapping." Having no dominoes certainly would not tile a 2 dimensional shape and since there is no way of tiling the 1 dimensional shape there is only 1 way to do it and that's not to do it.
Log in to reply
@Scott Schwartz – Yes, Steven is right in saying that there is 1 way to tile a "0 X 2" space, in order for our combinatorial identities to make sense.
For example, if the number of ways that you can tile a "0X2" space is 0, then the number of ways to tile a "0X2" space and then a "1X2" space is 0 × 1 = 0 by the rule of product.
Note: In a similar manner, the empty product is defined as 1.
Log in to reply
@Calvin Lin – I get what you are saying. Gotta love the Fibonacci sequence... and Phi too!
Here's the answer.
Solution
Amazing thing here is that it's like a fibonacci series.
Good observation.
Why can't these be the answers?:
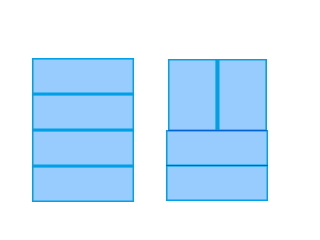
If I include these as the answers, then the total number of combinations will go from 5 to 7.
PS: Please tell me how to attach an image in the comments section. I did it with great difficulty! Went to the Community page>Add Note>Insert image> copied the link and pasted it here. Is there an easier way to do this?
Log in to reply
The question is about 4x2 but your way is 2x4
Ritvik Chaturvedi, why only these two you can also place all the cubes vertical and then there will be 10 but you need to analyse the question correctly. You need to follow the sequence in same way as the question did.
Solution to your second problem is that first of all post your image to any good image uploading website (i prefer http://postimage.org/) then copy the direct link provided by the website and then paste the link in comment section in the following format.
This is caption to the image
This is like the fibonacci sequence but starting from one. Given a 2xN area, you can place two horizontal pieces and have all the ways fot the area 2x(N-2) or place one vertical piece and have the ways for an area of 2x(N-1), we get the recurrence S n = S n − 2 + S n − 1 , S 0 = 1 and this means S n = F n + 1 where F n is the n-th fibonacci number.
It should be only 4 ways cos =|| is the same as ||= or that's what i think!!
Log in to reply
They've already demonstrated in the example (setting up 3" x 2" area using 1" x 2" tiles) that the order does matter. According to that example, |= and =| are different, so surely ||= and =|| should also be different. I don't know if this is completely correct, but that's my take on this..
-
We could place the first tile horizontally, which forces us to place another directly below it and so the empty area is now a 2 × 2 . There are 2 ways to tile this.
-
We could place the first tile vertically, so the empty area is now a 3 × 2 . There are 3 ways to tile this.
So there are 5 ways to tile a 4 × 2 area.
In general, the number of ways to tile a 2 × n area is the sum of the number of ways to tile a 2 × ( n − 1 ) area + the number of ways to tile a 2 × ( n − 2 ) area because we can apply this same process. This is, of course, equivalent to the Fibonacci sequence .
Observe that it is impossible to tile an odd number of vertical 1 × 2 dominoes in a n × 2 area such that n is an even number, and also it is impossible to place an even number of vertical 1 × 2 dominoes in a n × 2 area such that n is an odd number.
If we have 4 × 2 area to tile, there are 3 general cases according to the observation:
1 . Putting 4 vertical dominoes, we have ( 4 4 ) ways to do it.
2 . Putting 2 vertical dominoes, there are ( 2 3 ) ways to do it. The other horizontal domino counted as 1 box hence we have 3 boxes to place with the vertical dominoes.
3 . Putting 0 vertical dominoes, then there are ( 0 2 ) ways to do it. We have only 2 boxes to place horizontal dominoes as there are zero vertical dominoes.
Sum all of the ways, then there are ( 4 4 ) + ( 2 3 ) + ( 0 2 ) = 1 + 3 + 1 = 5 ways to do it. The general summation we've been looking for many ways n × 2 area to be tiled with 1 × 2 dominoes is: i = 0 ∑ ⌊ 2 n ⌋ ( n − 2 i n − i ) . For every n it may refer to fibonacci's sequence.
5 ways (IIII, =II, I=I, II=, ==)
and...
8 ways for 5"x2"
(IIIII, =III, I=II, II=I, III=, ==I, =I=, I==)
13 ways for 6"x2"
(IIIIII, =IIII, I=III, II=II, III=I, IIIII=, ==II, =I=I, =II=, I==I, I=I=, II==, ====)
21 ways for 7"x2"
(IIIIIII, =IIIII, I=IIII, II=III, III=II, IIII=I, IIIII=, ==III , =I=II , =II=I , =III=, I==II , I=I=I , I=II= , II==I , II=I= , III== , ===I , ==I=, =I==, I===)
1, 2, 3, 5, 8, 13, 21... it look like the Fibonacci sequence, isn’t it?