1, 2 or 3 stones?
You play a game with a friend with a pile of 20 stones numbered 1~20. You take turns taking 1 stone, 2 consecutive stones, or 3 consecutive stones out of the pile. For example, in your turn, you can take out (19) or (11, 12) or (7, 8, 9) if they are still there. The player who takes the last stone wins.
If you go first, is there a strategy that guarantees you a win?
Clarification
: The stones have to be consecutive, but they can be pulled from the middle of the group if you like. For example, on your first move, if you take out three stones, they don't need to be (1, 2, 3). They could, for example, be (11, 12, 13). And likewise for successive turns.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Moderator note:
There's some comments on attempts of generalizing the solution and the problem. I don't want to spoil all the fun, but I wanted to give a general tool for approaching this sort of problem when symmetry isn't necessarily being used.
With this game it's possible to sort the layouts into winning positions and losing positions . A winning position is one where a player presented with the layout is guaranteed to win with best play; a losing position is the opposite.
For example, looking at a single stone { 1 } is a winning position, since the player takes the last stone and wins!
On the other hand, two sets of 1 stone each (we'll call it { 1 , 1 } ) is a losing position, because no matter which pile the player picks, it turns the layout into a winning position for the other player.
{ 1 , 1 , 1 } is a winning position, since the current player can take 1 stone and force the losing position { 1 , 1 } on the other player.
In general, the idea is that winning positions are ones that can be turned into losing positions with a single move , and losing positions are ones where any move a player can do results in a winning position for the opposing player.
This allows a collection of winning and losing positions to be built up. { 1 , 2 } is a winning position because a player can force { 1 , 1 } (which we know is losing) whereas { 2 , 2 } is a losing position because the only possible moves leaving winning positions for the opposing player.
I found the same thing. It is only necessary to create two equal but separate piles then copy the opponent until it comes down to handing the opponent the losing 1- 1 combination. No need to repeat it on the top level.
This is far less involved than Nim which this game superficially resembles.
Ya nice solution sir.
Log in to reply
Thanks! :0) Follow up question... Is it the only solution? :)
Log in to reply
Okay. Let me think sir.
I think removing (2,3,4) leaves a winning position too.
Log in to reply
@Malcolm Rich – My mistake - I meant remove (2,3). Two piles of size 1 and n, the objective would be to always leave n = 1 (mod 4)
Log in to reply
@Malcolm Rich – Ah yes... I think you are right! And, of course, by symmetry, (18,19). Interesting!
Log in to reply
@Geoff Pilling – There are many "winning positions". I might even speculate that removing two stones from any position - except (1,2) or (19,20) - might win but this is certainly not a "basic" problem
Log in to reply
@Malcolm Rich – This game is a variant of Nim. At any stage there are a number of piles of counters on the table. At each go a player may remove up to 3 counters from one pile, and may also decide to split that pile into two not necessarily equal piles. The same starts with a single pile of 2 0 counters.
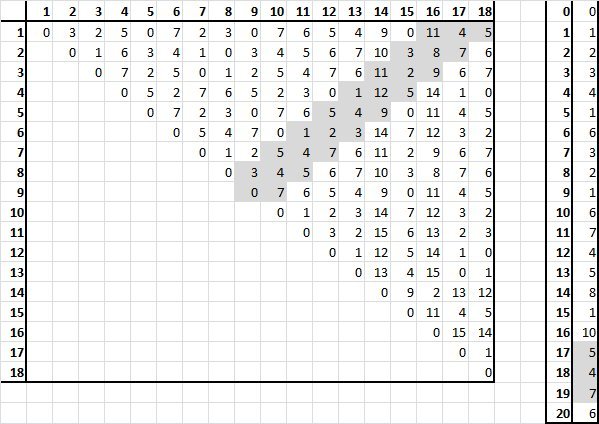
The RH column is the Sprague-Grundy number for this game for a single pile of n counters. All these numbers are nonzero (except the first) since it is always possible either to remove the whole pile or else leave two identically sized piles.
The LH table shows the Sprague-Grundy number for this game for two-pile scenarios. The only possible outcomes of an initial move from a single 2 0 counter setup are shaded in grey in these two tables. Note that only the move that leaves two piles of size 9 is a winning move. Every other first move would hand the game back to the other player!
Log in to reply
@Mark Hennings – I've not yet managed to figure out what the Sprague-Grundy number is yet or how you've calculated it. Could you elaborate a bit so that we can understand what the second player would do to leave themselves in a winning position - it which of their moves leaves a position with an SG value of zero.
Log in to reply
@Malcolm Rich – In any game of this type, a collection of piles can be assigned a SG number. This is 0 if the position is a losing one, and a positive integer otherwise. The SG number of a collection of piles is always the XOR sum (binary digit sum without carrying) of the SG numbers of each pile.
The SG number of a collection of piles is defined inductively as the "mex" of the SG scores of all the collections of piles that could result in one move of play. The word "mex" is short for "minimum excluded", so we want the smallest integer not in the list.
In this game, the empty board has score 0 . Consider setups with a single piles of size n . A pile of size 1 can only play to an empty board, so the SG score of a pile of size 1 is the mex of \0), and so is \1). A pile of size 2 can play to the empty board or a board of size 1 , with SG scores 0 and 1 respectively, so its SG score is 2 . A pile of size \3) can play to piles of size 0 , 1 , 2 , or two boards of size 1 , so the SG score of a piles of size 3 is the mex of 0 , 1 , 2 , 0 , namely 3 . And so on.
The key point is that if a board position has a nonzero SG score, then it must be possible to play to a position with a score of 0 . On the other hand, given a position with score 0 , it is not possible to play to a position with score 0 . Thus someone in a position with a SG score of 0 will lose, and someone faced with a nonzero SG score will win.
Given the table I worked out inductively, there is no play from the 2 0 pile position that puts the opponent in a position with SG score of 0 except the move that leaves the opponent faced with two piles of 9 .
Try Googling Sprague-Grundy, Nim, and see what you can find.
Log in to reply
@Mark Hennings – I'm trying to work out why the SG score is important. It feels more intuitive to me to score everything as either 0 or 1. A winning position is 0 and it holds that status by virtue of the fact that a) There is no move that can lead to another point with a score of 0, and b) for every possible move, there is a follow up move that leads back to a score of 0. Actually a) and b) are equivalent statements.
This particular problem is tricky given the number of options available at each move and seemingly winning positions turn out to be losing positions. While leaving (1,1) or (5,1) or (9,1) will win. I've realised now that the pattern breaks down at (13,1) because it allows a winning leave of (8,3,1).
It's a very complex game with lots of surprises
Log in to reply
@Malcolm Rich – Yes, if there were a way of scoring every position as 0 or 1 for lose or win, that would be great. What the SG scheme does is make it easier to calculate the score - the score for multiple piles is the XOR sum of the scores for the constituent piles, and that makes calculation easier -while still distinguishing winning and losing positions. The mex-based definition again makes it relatively easy to work out values for increasing large setups; for some animals variants the value of the SG function can be worked out precisely for all n , so the entire strategy can be determined.
Log in to reply
@Mark Hennings – I think I get it now. If we have two groups of piles with a score of A. It means that a move from the first will typically move to a new position with a score of B. I then compare the scores of the two groups and select the higher SG score. By definition, I can find a new position which is equal to the SG score of the other group.
By contrast, if the two scores for the groups don't match, you take the one with the higher score and find the move that matches the score of the other group.
I know this is not a rigorous proof but it makes sense.
Log in to reply
@Malcolm Rich – Not quite. If you start with a single pile of 5 stones, then you could end up with a single of 2 , 3 , 4 stones, or else piles of ( 1 , 1 ) , ( 1 , 2 ) , ( 1 , 3 ) , ( 2 , 2 ) stones. Using ⊕ to represent the XOR sum, the SG scores of these arrangements are 2 , 3 , 4 , 1 ⊕ 1 = 0 , 1 ⊕ 2 = 3 , 1 ⊕ 3 = 2 , 2 ⊕ 2 = 0 . The mex of 2 , 3 , 4 , 0 , 3 , 2 , 0 is 1 , and so the SG number of a single pile of 5 is 1 .
On the other hand, a starting position of ( 1 , 5 ) has SG score of 1 ⊕ 1 = 0 . This matches the fact that possible positions that can be reached from this starting point are 5 , ( 1 , 2 ) , ( 1 , 3 ) , ( 1 , 4 ) , ( 1 , 1 , 1 ) , ( 1 , 1 , 2 ) , ( 1 , 1 , 3 ) , ( 1 , 2 , 2 ) , which have SG scores 1 , 3 , 2 , 4 , 1 , 2 , 3 , 1 respectively, and the mex of these numbers is 0 .
This is why the XOR/mex business is useful. I could calculate the ( 1 , 5 ) SG number without going through the mex process - I could derive it from the SG numbers of 1 and 5 . We only have to work hard to calculate the SG numbers of single piles.
Log in to reply
@Mark Hennings – Yes. I was explaining why the SG score made sense in a more general case when there are multiple piles of stones. If those piles can be divided into two group, each with an SG score of, say 7. The XOR calculation yields 0 so I can't make move to another SG score of 0. The reason for this is that the scores for the two groups is defined in such a way that any move to either group can't land on an SG score of 7 -> XOR (7,a) is not zero.
But it also now helps find the correct response to that move. If a>7, I can find a move to give that collection of piles an SG score of 7. If a <7, I find a move to the other collection of piles to give that an SG score of a. In either case, XOR (7,7) or XOR (a,a) is zero.
In practice the winning player will make life easier for themselves by keeping track of groups of piles with a score of 0 - (1,1),(5,1),(3,2,1) etc - as each of those groups can now be seen as a self-contained game. But if the game has evolved differently, the general approach needs to be followed to stick to the winning strategy.
@Malcolm Rich – Interesting... I'll need to think about that for a bit... For example, does (3,4) win?
Log in to reply
@Geoff Pilling – I don't know yet because the ability to split groups of stones into two adds an extra dimension to the problem. We know that matching pairs of stones can allow a copying strategy buy what happens if they are three or five groups of stones. Leaving (1,2,3) always wins but leaving (1,1,5) will lose.
Log in to reply
@Malcolm Rich – That would make a great follow up problem... n groups of m stones... :0)
A straight forward and clear solution!
Too good, this one!
I started to see a pattern(AP) for which the nos. we could possibly reach to by eliminating necessary numerals... So, if we start with 1, we can eliminate it with 2 & 3 to reach at 4. Then it's just our game...Whatever happens know since 3 nos. or less have to be eliminated therefore we can always reach out till a distance of 4 units. Hence, if we are at numbers- 4,8,12,16 ; we'll always win. EXPLANATION: Since we want the other guy to be 17 or above(except 20), we want to be at 16. Now, we can also think of the possibilities of the other guy being at 13, 14 or 15; we notice that anyways we'll end up at 16 and thus verify down till 1. Hence we start with 4 and go to 8<12<16 and then easily win... This game is actually related to 21 dares...Although there we lose if we reach at 21... Therefore it is logical to conclude the trick holds for that game as well. As, the no. is decreased by 1 unit & it's not that we win at 20... This game is known as "Impartial Combinatorial" games.I believe that, essentially, you always want to leave the person with a "pile" of matches equal to 5, 9, 13, and/or 17. (In the counting game, that means YOU want to be the one to stop at 4, 8, 12, and 16. The earlier ones don't matter as much, as long as you make sure that YOU get to say "sixteen" and end your turn on it.) * EXTRA:: (21 dares. explained) It's easiest if the other person goes first. If the other person starts by only saying "one," you say the next three numbers ("two, three, four"); if the other person starts with "one, two", you respond with "three, four"); if the other person starts with "one, two, three," you say, "four." Now you're set for the rest of the game; keep eliminating by countering any move they make with a move of your own that brings the total of those two turns to FOUR.
If YOU go first, there's a chance that they will win (especially if they know the formula!). If I were to go first, I would say "1" to give myself the most leeway to make course corrections later on. I would just have to look for my earliest opportunity to steer the game so that I end a turn by saying 4, 8, 12, or 16.
Once you get to end your turn by saying "16," you've won. If the other person says "17," you say, "Eighteen, nineteen, twenty" (leaving him with the last one). If the other person says "17, 18," you say "19, 20" (leaving him with the last one). If the other person says ""17, 18, 19," you say "20" (leaving him with the last one).
Log in to reply
I think you've missed an important aspect of this game. It's not a simple count to 20 but one where you can remove stones at any point in the sequence.
For example, if you leave any single sequence of stones you will lose the game as your opponent can always extract 1 or 2 stones from the middle of this group. Once you see two matching groups you can't win.
Log in to reply
Thanks, Malcolm... I've clarified the problem statement. Do you think its more clear?
Log in to reply
@Geoff Pilling – The original question was, in my view, clear enough. If there was a trap, it was the way it might be interpreted or understood by drawing a link to a similar, but different, problem.
Dude, I don't know if this problem states the opposite of what I think it is..... Though I recommend you to view the solution once again. If you are trying to say clearing 1 or 2 stones, then i'm saying the fact that is held that we can still clear 1 or 2 stones to reach the desired destination as well. What I explained in the latter form was a variant to this problem, but the solution is not different. Eg. If we can eliminate 1,2 & 3 ; its the same as jumping from 1 to 4.... Read closely:- 1-->4 the other guy eliminates 4 or 5&4 or 4&6&5 :we can still eliminate 5 or 5&6 or 5&6&7 to reach to 8.... Similarly, for the rest of the game , the pattern continues...WE reach at 16 by eliminating WHAT?? U guessed right- 13 or 13&14 or 13&14&15... If we "REACH" At a specific pt. , then we have eliminated the previous 3 or 2 or probably just 1 no. Therefore the other person. is compelled to eliminate atleast one of the nos.:16,17 or 18... In the worst case scenario...the other dude eliminates just 16.... Thus, still we can reach 20 by taking down 17 , 18 , "and" 19 to finally get to no. 20
Log in to reply
@Praman Verma – I think you are suggesting that if you leave stones 1,2,3,4 then you would win. The difference with this game is that I can take 2,3 leaving you the option of taking either 1 or 4.
I HAVE READ THE QUESTION TWICE NOW... What I believe is that people dont see the similarities but the differences between variants of a particular question which causes differnces between the people who recognized the same in the 1st place...
The nos. don't matter which are taken out.....What matters is your response to the no. of stones taken out by the other guy... Hence, if the other guy takes out 1 stone; you must take out 3 stones the next time ...If initial response of other guy is 2 stones out ; then u take out 2 ;; if 1 taken out... you take out 3 stones ...in general: (4-n) is ur response... where n is 1,2 or 3...This strategy will always work out.. Anyways Thanks... :)
How can we be sure that there is a way to put each situation into einning and losing positions?
This is an example of Game theory and particularly "Game of Nim ". In a Nim game, there are n number of piles each having different number of coins let x i , where x i denotes number of coins in i th pile.
Now, in a normal Nim game, the player making the first move has a winning strategy if and only if the nim-sum of the sizes of the piles/heaps is nonzero. Nim-sum is defined as XOR (Exclusive OR) of heights of all piles. Mathematically , Nimsum= x 1 ⊕ x 2 ⊕ . . . ⊕ x n . where ⊕ denotes XOR operation.
Here after first move, we can divide the pile in at most 2 piles. Now if we divide it in equal parts, the Nimsum will be zero (as XOR of same numbers is zero). Hence, we can take stone number (10,11). Now, there are 2 piles (1-9) and (12-20). Whatever move the second player makes, we can make the same move and thus win the game.
Note--> After our turn, there are two piles (1-9) and (12-20).Now, the next move is made by the second player and according to him the nimsum is zero and that's why he is in loosing state.Our strategy is to put the other player in the loosing state.
Here are some links where you can learn more about game theory and XOR-->
It' takes a while but I think I follow it. Does it still apply when you can make a move that splits one of the piles into two new piles. Take (2,3,5) as an example with nim-sum=4. I believe that I would win if I left this pattern but it doesn't follow the rule.
Log in to reply
Actually, in original nim game , we can take any number of stones from a single pile.In the example where we have 3 piles of sizes 2 3 and 5, if we were allowed to take any number of stones from a single pile, we would have won but here in this question we can take at max 3 and at least 1 stone, so there is no way we can win. Let me illustrate both conditions (I assume you know about XOR)-->
case 1--> when any number of stones can be taken from single pile.
binary representations of 2 is 010, 3 is 011 and 5 is 101.Let us xor these:
0 1 0 ⊕
0 1 1 ⊕
1 0 1
− − − − −
1 0 0
100 is 4 in decimal representation. Now to make Nimsum zero, we need to make above nimsum zero which can only be done by taking 4 stones from the pile having 5 stones (which is effectively equivalent to making the MSB(Most significant bit) equal to 0 ). after that, we are left with piles having 2 3 and 1 stone and we will surely win as nimsum is zero(If we play optimally).
Case 2 --> when at max 3 stones and at least 1 can be picked.
Short summary --> Nimsum can't be applied directly in this case.
With this restriction imposed, we can't pick 4 stones and hence we can't make nimsum 0 as that MSB of 5 will always be set. Even the other player can also not pick 4 stones, so just to simplify game situation assume it to be 0 and consider that piles are of size 2 3 and 1 (as when we unset the MSB, it becomes 0).
We need to take at least 1 stone, so this would result in converting at least one of those two zeroes into 1.This would result in non-zero nimsum and this would be winning condition for other player.Now he can move to put us in loosing condition by making nimsum zero (IGNORE THAT MSB for now).After some moves, we will be left with following state of piles 0 0 4 and player to move next is us.Now whatever number of stones we take, the other player will win ie. if we take 3-->he will take the only 1 and so on....
What we try in these game is to put other player in loosing position (also called loosing state).
There are two rules in game theory-->
1.)From every winning position there is at least one loosing position.(That's once a player is in winning position, he can make some move and change game state to loosing position (by making xor sum zero) for other player )
2.) From a loosing position, we can move only to winning position.(that's why when a player is in loosing position, whatever move he play, it makes nimsum non-zero which will be winning state for the other player.
If you have any doubt, please feel free to ask as this topic is a little bit tricky and takes time to get comfortable with.
Log in to reply
In this particular game - which is not Nim - the 0,0,4 position loses since a player can remove the middle two stones of the 4-pile leaving 1 1 ->wins.
You're not wrong in applying game theory to identify and "win" position - such as 1,2,3 - that doesn't allow the opponent to find a win position. A lose position is one where the opponent can find a win position.
Those positions are just more complicated in a game like this with more options. The rule above still applies but it is harder to spot the winning positions and something can appear to be winning until the opponent finds their own winning move - eg dividing a group of 4 into 1,1
Log in to reply
@Malcolm Rich – Yeah Malcom, you're absolutely right. Actually when explaining the above cases, I didn't consider the condition of splitting, I was talking about general nim with restriction of picking at max 3 coins.this means that players take stones from the top of the pile not like in the question where he can pick from anywhere and split the pile.
When you asked for example 2 3 5, I thought you were asking for general nim with restriction of picking at max 3 coins but didn't consider split condition.My bad and I apologize for it.
For the given question, it is obvious that first player will win if number of stones > 0. if the number of stones is between 1 to 3, he can pick all the stones otherwise if the number of stones is odd then pick the middle one and if the number of stones is even then pick the middle two (like we did in the question).
I was just trying to explain the nim game in general (and may be lost track somewhere). :-) :-)
Log in to reply
@Divyanshu Bansal – I think those links were very interesting. The general Nim-sum law is a very elegant piece of maths and I at least know something I didn't know yesterday. What frustrates me with this problem is that I haven't figured out the general solution. Nim-sum = 0 always wins if you have pairs of equal size but doesn't always work - eg 5,4,1 can be moved to 5,1,1,1 which wins.
Log in to reply
@Malcolm Rich – Let me tell you something which is not written anywhere, actually when we are computing xor-sum (nim-sum),we are not using size of pile instead these are number of moves available for a particular pile.For eg. in standard nim we are allowed to take 1 to n any number of coins ie. if size of pile is 4 then we can pick 1 coin or 2 coins or 3 coins or 4 coins,so we have 4 moves.Hence, it is not size of pile instead number of moves but it appears like size of pile.
In our question we can't directly xor these number (5 4 and 1) we need to count number of moves.
when size is 1, we have only 1 move.
when size is 4, we have 5 moves which are as follows-->
Case 1) while picking one coin, we can the the split pile into piles of size (1,2) or a single pile of size (3) by picking corner coin.
Case2) while picking 2 coins, we can the split pile into piles of size (1,1) or a single pile of size (2) .
Case3) while picking 3 coins, we can have only one pile of size (1).
So there are total 2+2+1=5 moves.
Similarly for pile of size 5, we have 7 moves.
Now computing xor of 7 5 and 1 we get non zero value.Binaries are
1 1 1 ⊕
1 0 1 ⊕
0 0 1
− − − −
0 1 1
So, if we make pile of size 5 into size of 3 (which is effectively making it a pile of 4 moves), the xorsum becomes zero(as 111 changes to 100) and it puts the player in loosing position.New pile sizes are 3 4 1 and moves sizes are 4 5 1. Now, you can try any possible combination, first player will always win.Hope this makes things clear.
Log in to reply
@Divyanshu Bansal – I'm not sure what you're trying to show here. Leaving either 5,4,1 or 4,3,1 are both going to lose. In the first case, the opponent will remove the two centre stones from the 4 pile leaving 5,1,1,1 (in Nim-sum = 6 and wins). In the second case remove 2 stones from the 4 pile leaving 3,2,1 (Nim-sum = 7 and wins). There doesn't seem to be an obvious pattern.
Log in to reply
@Malcolm Rich – What I'm trying to say is that you can't xor 5 4 1 directly to compute result, you need to convert it to number of moves and then compute xor. For pile of size 5, we have 7 moves ; for pile of size 4, we have 5 moves and for pile of size 1, we have 1 move.So we will xor 7,5, 1 (not 5, 4, 1).
Xor of 7,5,1 is non-zero hence first player will surely win if he plays optimally. What you are doing is splitting pile of 4 in two parts of size 1 and 1 but what I'm saying is to split the pile of size 5 into a single of pile of size 3 (by taking two corner stones).
For a game with pile of size 5 4 1
State of piles of each turn-->
After first player's move--> 3 4 1
After Second Player's move--> 3 1 1 1
After first Player's move--> 1 1 1 1
After second player's move--> 1 1 1
After first player's move--> 1 1
After second player's move--> 1
After first player's move --> No stone left
Hence, second player can't make a move and loses
Log in to reply
@Divyanshu Bansal – When the piles are 3 4 1, the second player will leave 3 2 1 and win.
Log in to reply
@Malcolm Rich – Hmm, that doesn't seem to work here. I am trying to find a general solution.
This is not Nim. It resembles Nim but in is a rather degenerate form having a much simpler solution than Nim.
Have you ever seen the film Last Year at Marienbad?
Log in to reply
Yeah, it resembles nim. First player will win if number of stones > 0. if the number of stones is between 1 to 3, he can pick all the stones otherwise if the number of stones is odd then pick the middle one and if the number of stones is even then pick the middle two (like we did in the question).
But haven't found a general solution for n such piles having x number of stones (necessarily not same).
Malcom Rich and I were trying to find a general solution for n such piles having x number of stones (necessarily not same). Though we haven't found yet...But will share if we make some progress.
I haven't seen that movie. Is it related to this question?? I will see it when I get some time...
My first turn I take one stone: number 20
why start with 20? Why not some other number?
If you take 20, then player two will take 10, and you lose since you now have two "equal" groups, 1-9 and 11-19. So, now whatever you take out of one group, he can take out of the other, and win by taking the final stone!
The first one ALWAYS wins. The key is to keep symmetry. First, pick the central stone(s), make sure you left two same groups of stones. In your opponent's turn, he must choose one group to pick, then we just keep symmetry, make the other group completely the same as the picked one. Then, there's still two same groups of stones, the process repeats...in the end, one group was taken out by your opponent, you can make the last move. This game reminds me of Zugzwang in chess...
Anyone heard of the game 21 dares? It works so that the person who says 21 is the loser. If you play in a two there is a strategy to always win if you start second. If you get the number '4', then you will be guaranteed a win
this is how it would work out: (Each turn is separated by a comma) 1 2, 3 4,5 6 7, 8, 9, 11 12, 13 14 15, 16, 17 18 19, 20 try any combination with you ending your turn on a multiple of 4-
Relevant wiki: Combinatorial Games - Winning Positions
If you take stones 10 and 11, you leave two "blocks" of stones with 9 stones each, namely 1-9 and 12-20.
Now, whichever group he takes from, you can take the corresponding stones in the other group (N-11 or N+11) and you are guaranteed to eventually take the last stone! :0)