1-D Relativistic Dynamics
A relativistic particle is projected from the origin at time t = 0 with initial velocity v o . The particle experiences a constant force of F . Compute the time at which the speed of the particle is 0 . 9 c .
Notes:
-
Rest mass - m = 1 ; Initial velocity - v o = 0 . 1 c i ^ ; Force - F = 1 i ^ ; Speed of light - c = 1 . Here i ^ is the unit vector along the X-axis.
-
Hint: Recall the expression for the linear momentum of a relativistic particle.
-
This problem should have been labelled as easy.
Bonus: Compare the motion of the particle to the non-relativistic case for the exact scenario.
The answer is 1.96425.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
We are still talking about time in a perfectly ordinary way, despite the dynamics being different. I have thus far simply assumed that we can do so, without making reference to exotic notions like "proper time" or "time dilation" or anything. Have you looked into that aspect of it?
Log in to reply
That is a good point. As a matter of fact, even I have assumed the same. Phenomena like time dilation and length contraction are dependent on the frame of reference. Since we are not dealing with any kind of relative motion so far, I think it is okay. But I will look further into these concepts.
Will there be a higher-dimensional version coming?
Log in to reply
I came across some open source material on this subject that I intend to study.
https://link.springer.com/content/pdf/10.1007%2F978-981-13-1090-4.pdf
I could easily make a problem like like the last two, where we, the observers are in an inertial frame of reference. It just boils down to applying a modified version of Newton's second law. I am thinking on the lines of a relativistic pendulum. So far I do not even know how to wrap my head around this, but I will try. Should be fun. Will post as soon as I have a meaningful solution to it.
Eventually, I'd like to start introducing moving frames of reference as well, but baby steps for now. These concepts will take me time to fully grasp.
Log in to reply
I've started looking at this link for relativistic Lagrangian mechanics, in anticipation of problems like the relativistic pendulum. The examples provided at the end are helpful.
https://en.wikipedia.org/wiki/Relativistic Lagrangian mechanics
The tricky thing seems to be that the "kinetic energy" term in the relativistic Lagrangian is different from the general relativistic kinetic energy.
Log in to reply
@Steven Chase – Indeed, I read a little bit about this too. It is quite interesting that the simple notion of L = T − V does not hold.
Log in to reply
@Karan Chatrath – I think I may post a relativistic kinematics problem, and see if the Newton and Lagrange methods match
Log in to reply
@Steven Chase – Thanks for posting. I will share my solution after some time, as it is late in the night at my end. In the meantime, I could not figure out the relativistic pendulum problem as the treatment of gravity in relativistic mechanics is quite different. We cannot use the classical approximation of gravitational Potential energy ( m g h ). I will post a relativistic oscillator (spring-mass) problem soon, however.
I posted an alternate solution to your problem "Hypothetical Relativistic Oscillator", it was a fun problem; thanks. Check it out!
Start with the relativistic momentum:
p = c 2 − v 2 m c v
Relativistic Newton's 2nd Law (there are no vectors, since the problem is one dimensional):
F = d t d p F = c 2 − v 2 c 2 − v 2 m c v ˙ − m c v 2 1 ( c 2 − v 2 ) − 1 / 2 ( − 2 v v ˙ )
Simplifying results in:
F = ( α + β ) v ˙ α = c 2 − v 2 m c β = ( c 2 − v 2 ) 3 / 2 m c v 2
The rest is just number crunching. In the non-relativistic case, the acceleration would be 1 and the particle would reach v = 0 . 9 c at t = 0 . 8 . It takes considerably longer in the relativistic case because relativistic particles behave as if they have mass greater than their rest mass.
I also tested this with my general 3 D relativistic mechanics solver, and the results were the same.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
|
@Steven Chase Hii . Sir i was making a question but can't able to solve. Can you help him??
Hello. What is the question?
Log in to reply
@Steven Chase
I have added the photo of question by writting it in my Notebook
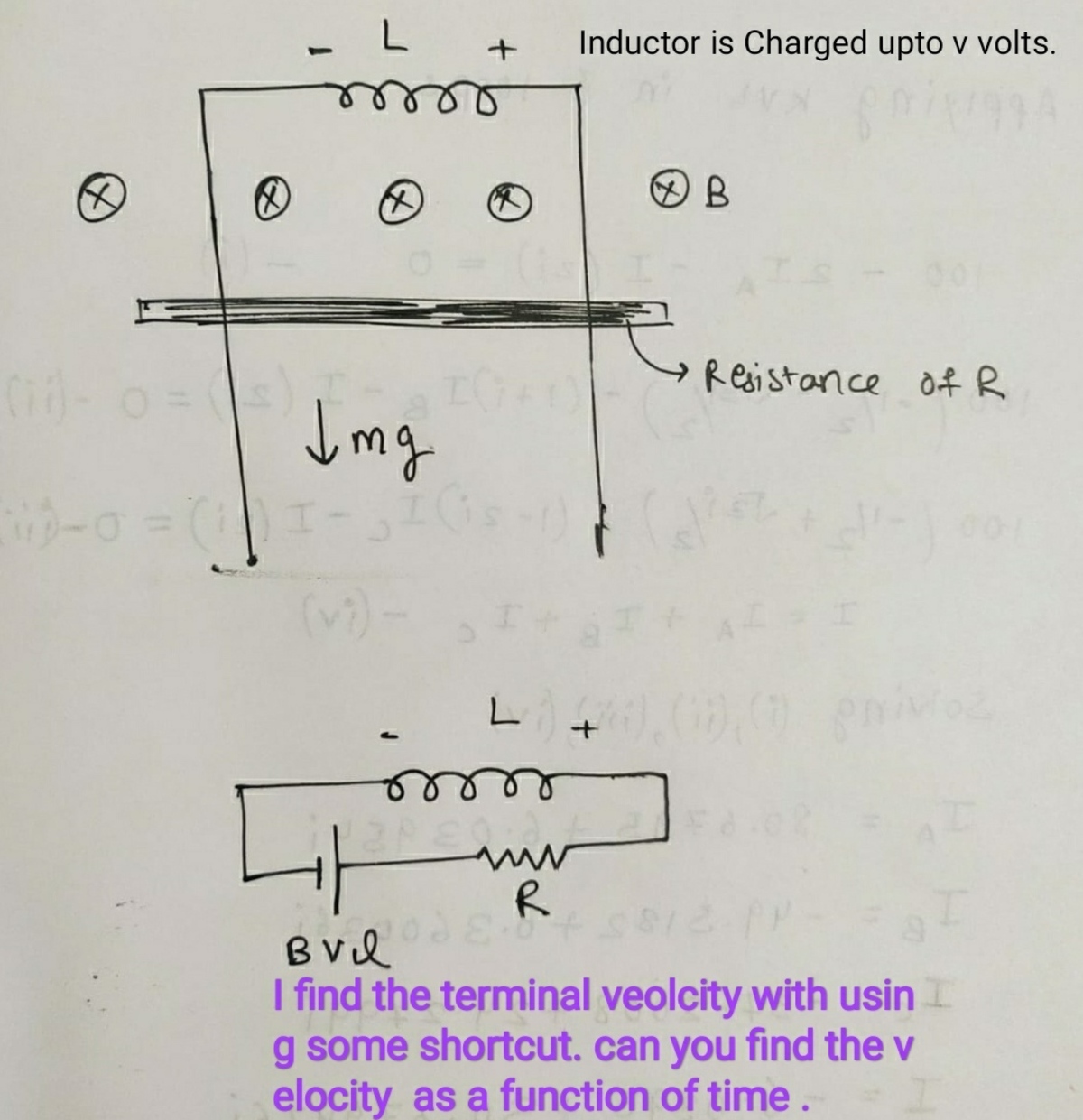
Log in to reply
These equations seem to yield sensible behavior.
B ℓ v − R I = L I ˙ m g − I ℓ B = m v ˙
When I simulate this, the current and velocity of the mass undergo damped oscillation before settling into steady values.
Log in to reply
@Steven Chase – @Steven Chase I am getting V t e r m i n a l = B 2 l 2 m g R is it correct?
Log in to reply
@A Former Brilliant Member – That's what I get as well
Log in to reply
@Steven Chase
–
@Steven Chase
I am getting this equation
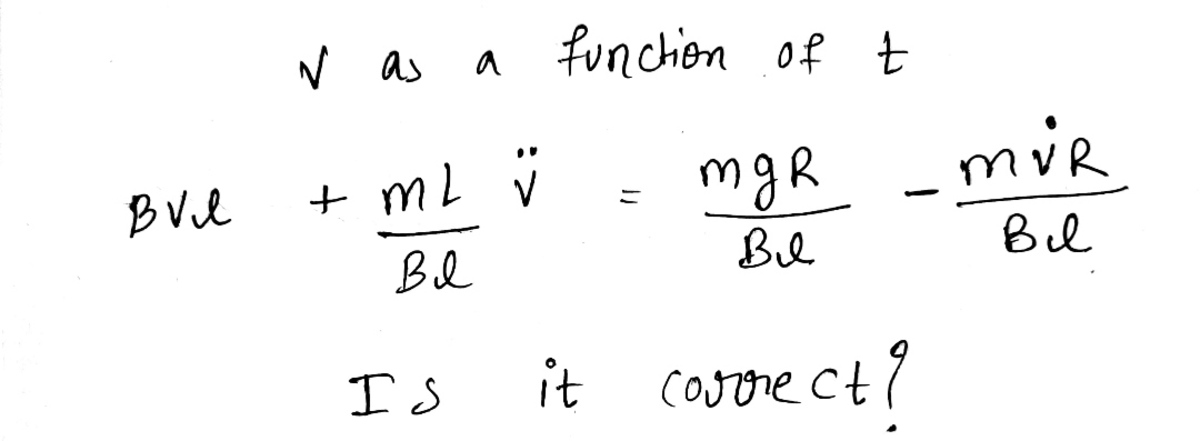
This is a non-homogeneous, coupled set of differential equations. Possible to solve analytically, but it's a hassle. Much easier to just solve numerically
@Steven Chase I was making one more question. But can't able to solve? Can you help me?
@Steven Chase the question is that I have n sided polygon. The length of each side is 1 unit. At all n vertices a charge + q is placed. Find the charge that I should place at the centre so that system will be in equilibrium?
Log in to reply
Once you pick a definite number of sides, that one should be fairly easy to solve
Log in to reply
@Steven Chase – @Steven Chase yeah that's why I don't want to pick it . H a H a H a . I want to generalise.
@Steven Chase – @Steven Chase The reason behind this is that my some friends get stuck while solving this in square, Hexagon. I want to tell them the formula and remove their problem forever.
@Steven Chase Sir can you post a question which is a type of 1st question which I asked today. I like that kinds of problem very much. . The problem should be very very advanced. Because I can't able to make that type of question.
Log in to reply
I think the problem you proposed is a good one. Especially when the dynamics are considered
Log in to reply
@Steven Chase – @Steven Chase Sir but I am expecting more advanced version of this problem from you because you know physics better than me.
@Steven Chase Sir I like this type of problem very much. Can you make it more advanced and post a question. https://brilliant.org/problems/parabola-charge-stasis/ and thanks for this problem also. While it's very old but I like it.
An alternate solution from that provided by @Steven Chase.
Newton's second law reads:
F = d t d p ; p = c 2 − ∣ V ∣ 2 m c V
Applying the above to the given scenario results in:
d t d ( 1 − v 2 v ) = 1
Since: v ( 0 ) = 0 . 1 , solving the above differential equation gives:
1 − v 2 v − 1 − ( 0 . 1 ) 2 0 . 1 = t
Solving for t when v = 0 . 9 gives the result:
t = 1 9 9 − 9 9 1 ≈ 1 . 9 6 4 2 5
The reason I asked the bonus question was to show that in the non-relativistic case, the particle's speed exceeds that of light, which in reality is impossible.