1 green, 2 blue, and 3 reds

Put the green anywhere. Now, consider all the ways to put the blue:
1. One opposite the green and the other anywhere else.
2. Two blue adjacent to each other. (None of them opposite to the green)
3. Two blue opposite to each other.
Now put the red.

There is 1 way you can have three reds all adjacent, and 2 ways you can have two of the reds be on opposite edges (distinguished by whether the green is opposite the third red or not). That gives,

$1 + 2 = \boxed3$

Use Burnside’s lemma

(Scroll down to “Example application,” which is a less constrained version of this problem.)

The total number of ways to color an unmoving cube, given the constraints, can be computed by considering which sides to color green or blue (letting red take care of itself). This gives 6 * C(5,2) = 60 colorings, and all of these, trivially, remain invariant under the identity transformation.

Among these 60, the only ways to color the cube and have it be invariant after some actual rotation are under the three possible 180° rotations. For each of these three transformations, there are two opposite faces that remain in the same position, and one of these has to be chosen from the set of three red faces, while the opposite, unmoving face has to be the green one, so there are only two ways to color these two opposing faces. As for the moving faces, they have to be alternating red and blue — matching on opposite sides — so once you’ve decided which of the two colors to use on any of these four remaining faces, the three remaining ones are determined.

So there are three 180 degree rotations, each of which has 2*2 = 4 invariant colorings. Now adding colorings for the identity transformation, and dividing by the 24 possible rotations on the cube — we exclude the other 24 transformations that turn the cube inside out — we get:

(1 * 6 * C(5,2) + 3 * 2 * 2)/24 = (60 + 12)/24 = 3

You need note that the faces which aren't coloured green or blue must be coloured red. (1)

This means that the number of distinct ways to colour the whole cube (with 1 green face, 2 blue faces and 3 red faces) is the same as the number of distinct ways there are to colour one face green and two faces blue, because of (1). (2)

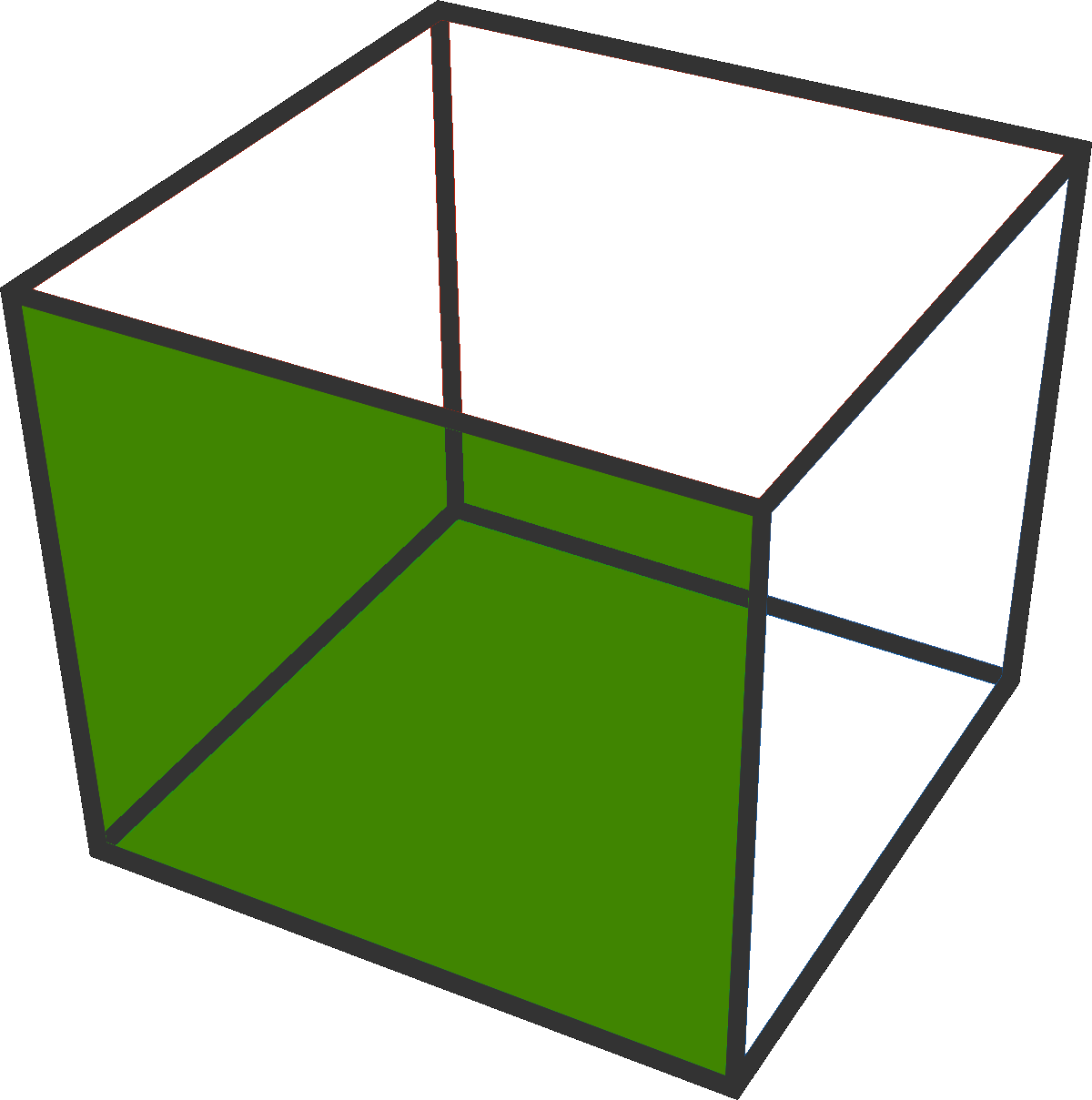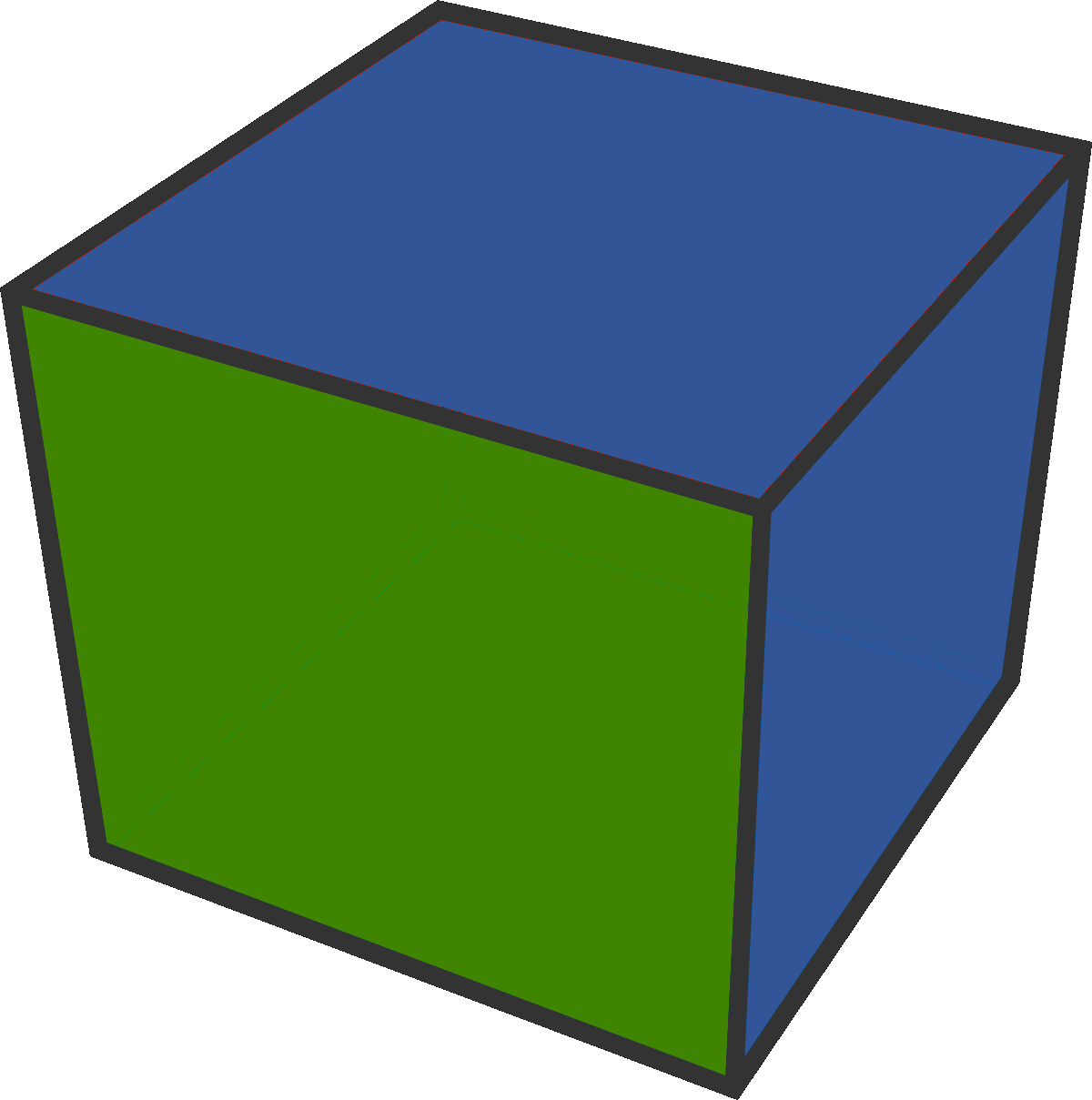
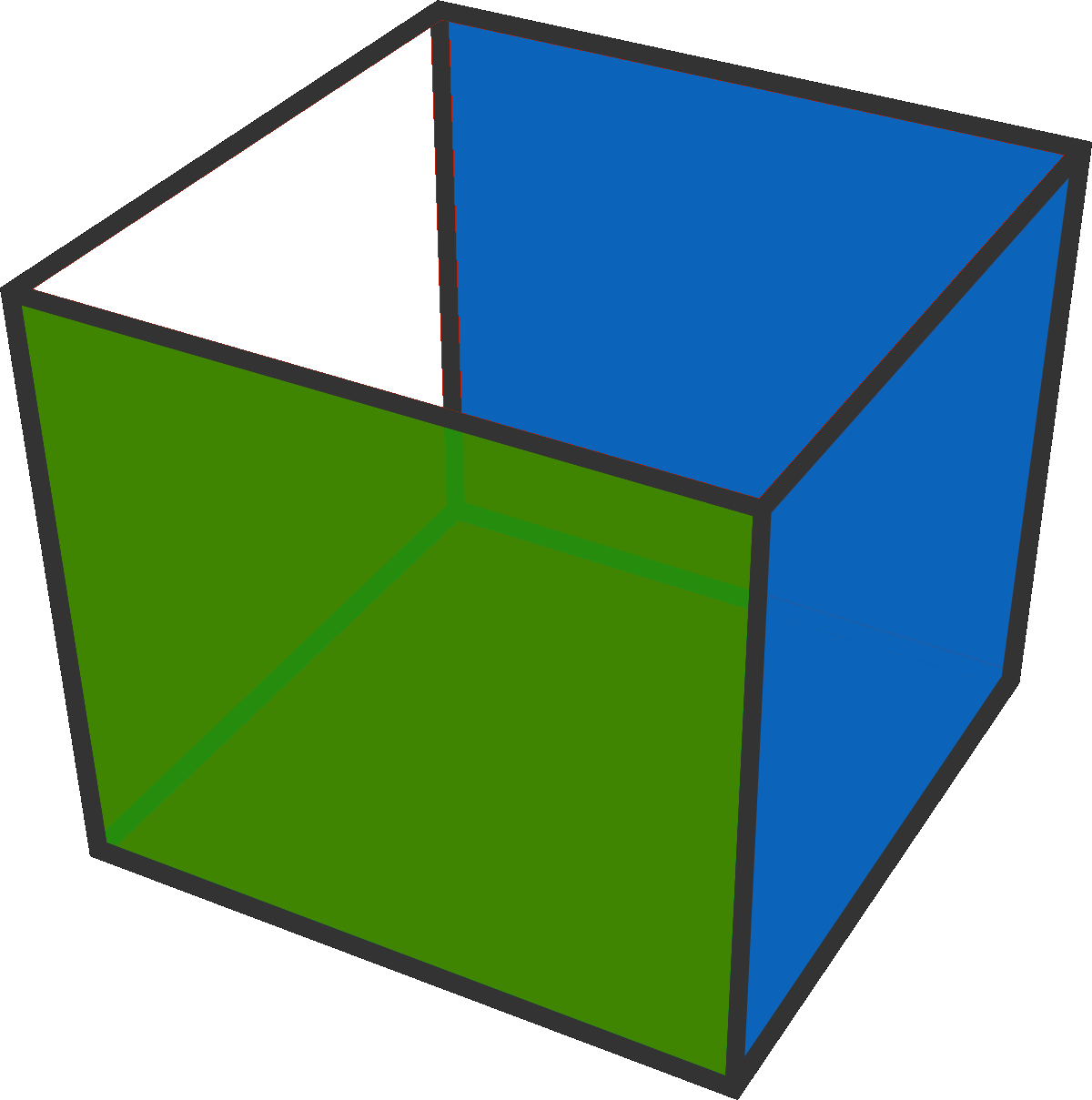
Take a cube with only one face green. Whichever face is green, the cube can be rotated to match all 5 other possibilities. Therefore there is only one distinct way to colour a cube with one green face. Now we can consider the two blue faces: 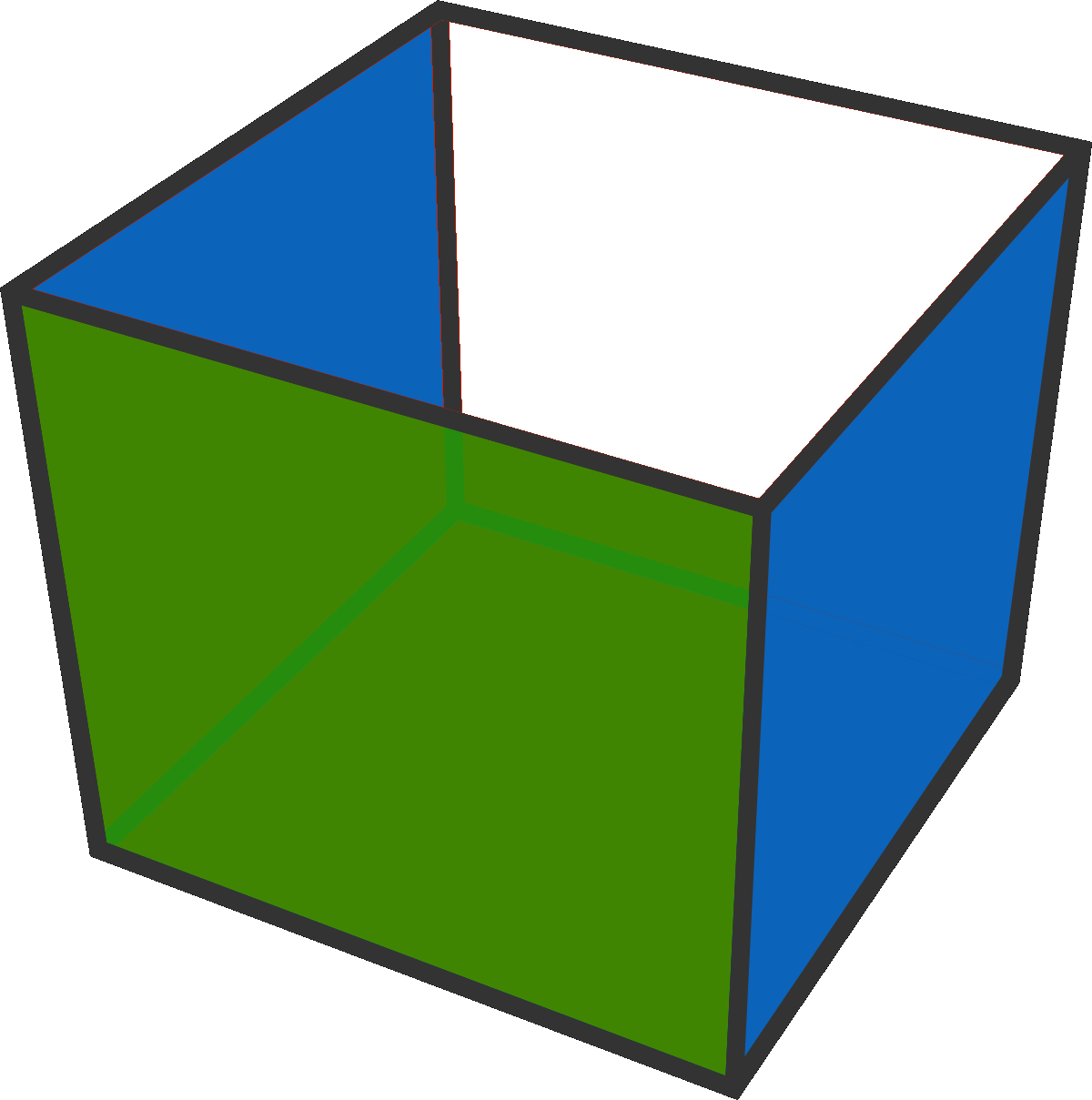As you can see, there are 3 distinct ways to colour 1 face green and two faces blue.

Because of (2), there are $\boxed{3}$ distinct ways to colour a cube with 1 green face, 2 blue face and 3 red faces.

First, decompose the cube as shown above. Then, fix the lower square of the unfolded cube to be the green and cut it from the figure. We are left with a very symmetric and easier figure to work with: 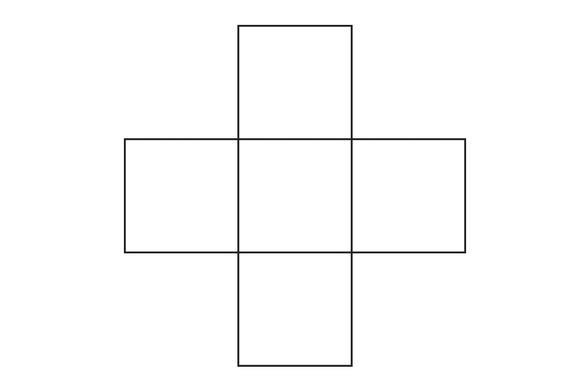How many ways are there to color this $5$ -square figure with 3 red squares and 2 blue squares? Simply, there are ${5 \choose 2}$ = ${5 \choose 3}$ = $10$ possible ways to paint the figure: 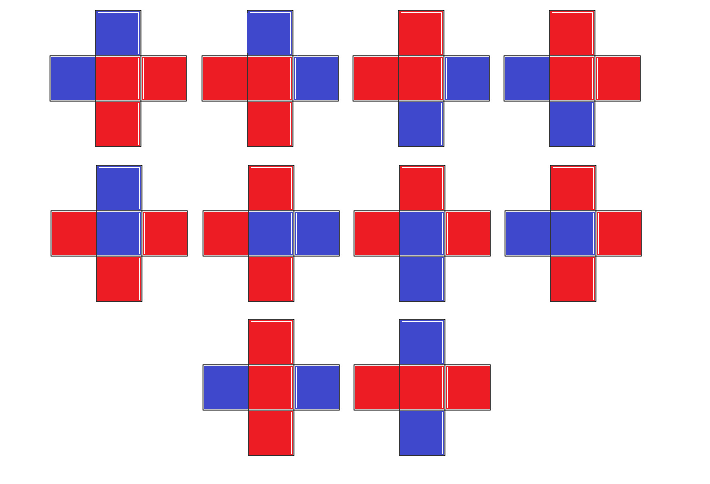We notice that the first row's elements are the same pattern, but the last three elements are just rotations of the first element. The same follows for row two's elements and row three's elements. So the total number of distinct cubes is the total number of distinct patterns of this figure which is, of course, 3 .

1. No matter how you choose the read sides, you can always rotate the cube such that there it is red on to and at the bottom. Where you place the 3rd red dose not make a difference, as you can always rotate the cube such that it is in front.
2. You can now chose one of the 3 remaining sides to be green and the rest will be blue. This gives 3 distinct ways.

Green can be opposite blue, leaving blue-red-red-red for the remaining faces;

or green can be opposite red, leaving either blue-blue-red-red or blue-red-blue-red for the remaining faces.

That makes for a total of $\boxed{\text{three}}$ solutions.

The way I did is imagine stationary

Now the are the types of different ways to arrange blue(red arranges itself accordingly)

1 both blue connected to each other as well as green side

2 both blue connected to each other but one on opposite side of green

3 both blue opposite to each other

Let's consider the green face fixed. The opposite face can either be red or blue.

If the opposite face is blue, the only distinct configuration is one in which the green face has three red neighbors and one blue.

If the opposite face is red, there are two distinct possibilities. First is that the red faces are next to each other. Second is that the red faves are opposite each other.

This totals to three ways to color the cube as described.

Only three sides are visible at a time as per figure

My solution is similar to Alon's, except that I worked with the 3 reds and 1 green. The 2 blue faces are automatically determined once the red and green faces are chosen.

There are only two ways to use the three reds.

The first choice of red faces is to have all 3 red faces meet at one vertex, which I will call the red vertex. With that choice, imagine the cube is like a top with the axis going through the red vertex through the center of the cube to the opposite vertex. Look at the three unpainted faces. No matter where you paint the green face, the top can be rotated through the axis I described so it looks the same. This choice of reds produces one painting of the cube.

The second choice of red faces creates a red "U" shape made out of the strip of 3 red faces. Set the cube on the red face that is at the bottom of the "U." Then you have only two distinct choices for the green face: either you bridge across the vertical arms of the "U" or you paint one of the sidewalls green (which can easily be rotated into one another). This choice of reds yields two paintings of the cube.

All this shows that there are a total of 3 possible paintings of the cube.

Using Graph Theory :

You can construct graphs to represent each possible configuration of red, blue and green faces of the cube.

Vertices represent the colour, edges show the colours of the faces opposite each other on the cube and the order of a vertex is the number of faces on the cube with that colour.

Therefore, we must have 3 vertices, labelled R (red), B (blue) and G (green), with vertex R having order 3, vertex B having order 2 and vertex G having order 1. The problem is now simply just how many distinct graphs can be constructed that satisfy these conditions. The answer is 3 .

Colour the near face green and think about how the two blue faces can be placed. Once the green and blue faces have been assigned the reds will take care of themselves!

You could place the blues top and bottom or left and right. These two options count as one because rotating the cube by 90 degrees around the centre of the near face switches the position of the blues while leaving the green unchanged.

Or you could place the blue faces bottom and left, or left and top, or top and right, or right and bottom. These four options count as one because starting with the first one, 90 degree rotations through the centre of the green faces take you successively through the four possibilities.

The only remaining case is to make the far face blue. Then we have four options again. The blue faces can be far and left, or far and top, or far and right, or far and bottom. Again these four options count as one because starting with the first one, 90 degree rotations through the centre of the green faces take you through the four possibilities.

And so we see there are just $\boxed{\text{3}}$ ways to colour the cube.