100 followers special
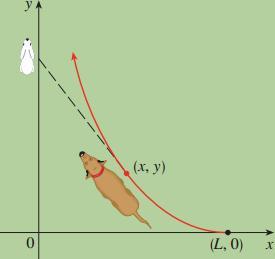 A dog sees a rabbit running in a straight line across an open field and gives chase. In a rectangular coordinate system (as shown in the figure), assume:
A dog sees a rabbit running in a straight line across an open field and gives chase. In a rectangular coordinate system (as shown in the figure), assume:
(i) The rabbit is at the origin and the dog is at the point ( L , 0 ) at the instant the dog first sees the rabbit.
(ii) The rabbit runs up the y -axis and the dog always runs straight for the rabbit.
(iii) The dog runs at twice the speed of the rabbit.
Assuming L = 3 0 0 units, how much does the dog have to travel to catch the rabbit?
Enter your answer as the distance the dog has traveled from sight to meal.
The answer is 400.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
How did you get the 2v-vcos(theta)? Wouldn't it just be 2vsin(theta)?
First of all, I'd like to thank all the 100 followers that have seen me as worthy of being followed. I have more awesome problems coming up in the future, so STAY TUNED XD
And now, a tribute:
 ss
ss
Hope that's all the time for you.
So, back to our problem. I'd like to see if this problem is fool-proof (no shortcuts or weird tricks). This is actually the 4th part of the question, and thus having skipped the first 3 that guide to answer the 4th, making it more difficult. But it's not impossible to answer this question without answering the first 3.
I've taken this problem from the Differential Equations chapter of Stewart's Calculus 6E. It will be posted somewhere on a wall in my school for a 50$ prize. Obviously this is directed towards the math teachers (for reasons), whom I wish to embarrass. I know cannot handle anything of this difficulty. But I can (with the solutions manual at my disposal xD).
So please check this out for me and tell me if it is a difficult one. (I didn't exactly dive into it, just skimmed). The solution sure seems not straight-forward. Here are the 3 sub-problems for those who are wondering:
The posted problem (here's the exact wording: Suppose that the dog in Problem 9 runs twice as fast as the rabbit. Find a differential equation for the path of the dog. Then solve it to find the point where the dog catches the rabbit. ) is a modified continuation of the original problem, where in the original the dog is as fast as the rabbit.
(a) Show that the dog's path is the graph of the function y = f ( x ) , where y satisfies the differential equation
x d x 2 d 2 x = 1 + ( d x d y ) 2
(b) Determine the solution of the equation in part (a) that satisfies the initial conditions y = y ′ = 0 when x = L . [ Hint : Let z = d y / d x in the differential equation and solve the resulting first-order equation to find z ; then integrate z to find y .]
(c) Does the dog ever catch the rabbit?
I shall post solutions upon request.
Cheers
Log in to reply
So that's how you solved it, huh. Yeah I saw the link. That's pretty disappointing :/
I guess there is no way to make someone go through all these steps with just one problem after all.
Log in to reply
John, when One Top referred to this book and solution, and I looked it up, I recognized the book as one of mine in my pile of books in the garage somewhere. One of these days, I need to go pull out all those books, and then I'll have even more fun on Brilliant.
But in fact, it turns out that the ratio of the speeds of the dog and rabbit is cirtical. If it's exactly 2 to 1, then as readily solvable as shown in that book. Otherwise, the solution gets less neat. The "straight line pursuit problem" is probably the most basic pursuit curve problem there is, and already it's a really messy problem. It might interest you to know that the Air Force do have extensive studies on the problem of pursuit curves, for I guess pretty obvious motivations.
Log in to reply
@Michael Mendrin – oo rlly? cause doesnt determining how far it travels also determine where it catches it? mhmeh then I could make it a general problem for when the dog is n times faster! but then I doubt solutions will exist LOL
but yeh if you wanna have fun on brilliant just wait till I have vacation I'ma pull up my communist russian math books with calculus math problems that some of great math professors of the time have struggled with! but now I'm taking a break. I will not be returning to brilliant probably for a year, or occasional vacations. maybe conceptual physics once in a while.
thx for all
Log in to reply
@John M. – John, if the rabbit has gone 200 feet (in your problem) before the dog catches ujp with it, then obviously the dog went 400 feet.
Please refer to "Ingenious" by L.A Graham, Problem #74 called Fido-Tabby Chase. This book is available on the net here: http://www.scribd.com/.../Ingenious-Mathematical-Problems...
Log in to reply
oh whoa what a huge shortcut! No complicated calculus whatsoever! dang, thanks a lot! This problem isn't worth 50$ after all (I even wanted to make it 100$).
And a great link by the way! You should share it as a note.
Cheers
Sorry for being picky, but your use of the word "displacement" confused me momentarily. I still entered the distance the dog traveled, (400 units), as my answer, but displacement is a vector, and in this case the displacement vector "from sight to meal" would have a magnitude of 2 0 0 2 + 3 0 0 2 = 3 6 0 . 5 6 units to 2 decimal places.
Log in to reply
O-oh? I thought displacement is how much an object goes through space, no? Or is it the distance from point A to point B ?
Log in to reply
The magnitude of the displacement vector is the 'straight line' distance between the starting and finishing points, i.e., from point A to point B . Since the dog travels along a pursuit curve he travels a distance greater than the magnitude of the displacement vector. At least that's how I was taught. :)
I figured that you wanted the distance traveled, since the answer had to be an integer, and in this case the magnitude of the displacement vector is not an integer but the distance traveled is.
Log in to reply
@Brian Charlesworth – Mhm I see. I will review this further and change the problem accordingly.
Thank you.
Log in to reply
@John M. – Your welcome. The solution Michael references is a nice surprise; I'd never seen it done like that. Anyway, according to the equation at the end we have the rabbit traveling
2 2 − 1 2 ∗ 3 0 0 = 2 0 0 units,
so since the dog runs at twice the speed it will have covered a distance of 4 0 0 units by the time it catches the rabbit.
Plz can you post some detailed solution which is simple


Yes I agree with Ronak.There is a similar question in IE Irodov.
d x / d t in the rate at which separation between dog and rabbit decreases. From the figure in vertical direction
− d x = ( 2 v − v c o s θ ) d t
∫ 3 0 0 0 − d x = ∫ 0 t ( 2 v − v c o s θ ) d t
3 0 0 = 2 v t − v ∫ 0 t ( c o s θ ) d t ..........(1)
in horizontal direction
v t = 2 v ∫ 0 t ( c o s θ ) d t
∫ 0 t ( c o s θ ) d t = 2 t
putting this value in eq (1)
3 0 0 = 2 v t − 2 v t
t = v 2 0 0
On multiplying this velocity of dog we will get the distance= 400