1/3 is a nice number for this case
Circles L and l share the same center. Circle L has radius 3 r and circle l has radius r . Points A , B , C are chosen on the circumference of circle L uniformly at random.
What is the probability that the centroid of △ A B C lies in the interior of circle l ?
The answer is 0.25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I don't agree with 1/4. If each point is equally likely to be chosen, then any point within circle L can be the centroid of triangle ABC. Going along with this, then we only need to find the ratio of the two circles' areas, which isn't 1/4. A ratio of two areas, l/L, would give 1/9. Granted, this would be the limit of that probability because you can only get the centroid of triangle ABC so close to the edge of circle L. If my logic is incorrect someone enlighten me.
Log in to reply
Any point inside L could be the centroid, but different points are not equally likely. You are assuming the the location of the centroid is uniformly distributed over the circle L , which is not the case.
Log in to reply
That makes sense, more triangles can have a centroid towards the center of L. Thanks!
Why do you multiply the integral by 1/pi?
A solution with no calculus! Say r = 1. Start with 1 point of the triangle, and call it A. Centroid is 2/3 s of the way from A and the midpoint of the opposite side. Note, now, that given any point inside the circle, there is a unique set of 2 other points such that the two other points' midpoint is the given point. If the centroid is inside the little circle, then the midpoints of the opposite side must also be in a tiny circle as well, even further from A, with area 2/3. To find the probability, we just consider the position of the midpoint of the opposite side. Thus, we have a r e a − o f − b i g − c i r c l e 2 / 3 , which becomes 1/4. (area of big circle is 9)
Here's a no-calculus proof. Each point divides the big circle into two semicircles (using the diameter through that point). To be in the arc diametrically opposite to the minor arc A B , the point C has to lie in the semicircle defined by A that does not contain B (this happens with probability 2 1 ) and also in the semicircle defined by B that does not contain A (this happens with probability 2 1 ). It turns out that being in the opposite A -semicircle to B and being in the opposite B -semicircle to A are independent events, and hence the probability that both events happen is 2 1 × 2 1 = 4 1 .
Yes, the centroid will lie in the small circle if the midpoint of the other two vertices lies in a circle of area ( 2 3 ) 2 π = 4 9 π , whose area is 4 1 of that of the big circle.
What you seem to be assuming is that the midpoint of the other two sides is uniformly distributed over the big circle. It is not.
Great solution! The only thing I can't understand is this: "Given any point inside the circle, there is a unique set of 2 other points such that the two other points' midpoint is the given point.". While it makes some sense intuitively, is there a way to prove it?
A graphical simulation of the problem.
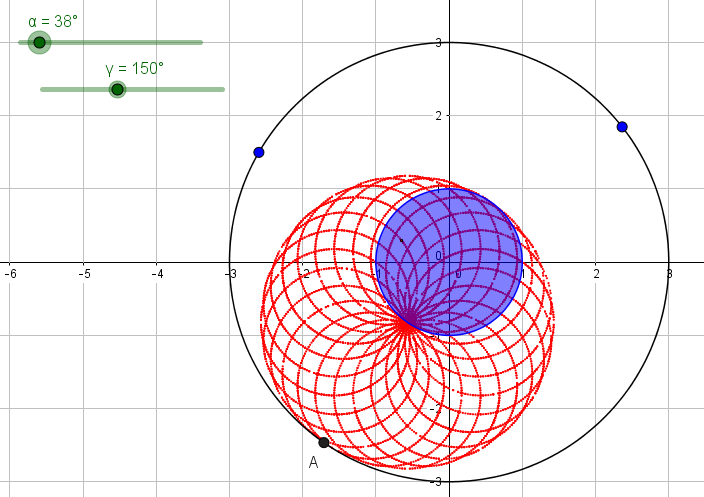 For a fixed point A, generate the locus of the centroid for different positions of the other two vertices of the triangle.
The centroid is located within a circle of radius two, which contains the target circle of radius one.
Ratio of these areas is therefore 4:1, giving a probability of 0.25.
For a fixed point A, generate the locus of the centroid for different positions of the other two vertices of the triangle.
The centroid is located within a circle of radius two, which contains the target circle of radius one.
Ratio of these areas is therefore 4:1, giving a probability of 0.25.
You are assuming that the location of the centroid is uniformly distributed over its locus. This is not true.
I guess that is apparent from the density of red at the centre of the red area. But then why does this still give the correct answer??
Log in to reply
It's intriguing, isn't it? Ex Money had a different take on the problem, assuming that the midpoint of two sides was uniformly distributed over the large circle, and again obtained 4 1 for the wrong reasons. However, in both cases, the probability that a particular point lies in a region involves averaging the probability (technically, integrating the probability density function) of the point occurring everywhere in the region. It just so happens that this process of integrating probabilities gives the same answer as if you assumed that the points were distributed uniformly. This would not be the case if you changed the radius of the smaller circle.
Log in to reply
In that same train of thought, if we let f ( r ) be the cdf for the probability that the point lies in the circle of radius r , then we know that f ( 0 ) = 0 , f ( 2 ) = 1 . We would love to claim that f ( r ) = 4 r 2 by a geometric argument, but in order to do so, we have to consider where these "centroid points" lie.
For a visual simulation of this difference, model the location of 100 (or 1000) of these centroid points. You will notice that they tend to be clustered around the center, as opposed to around the sides. As such, the density of these centroid points is
Follow up question: Can we determine f ( r ) ?
Note: The red points are too regular (they form many circles!), which suggests to me that you are taking fixed variations of B and C, as opposed to truly random ones. Even then, the difference becomes "apparent from the density of red at the center of the red area."
Log in to reply
@Calvin Lin – Assume that the point A is fixed, and that B and C are uniformly and independently distributed over the circle. Let A D be a diameter, and let X be the midpoint of O D .
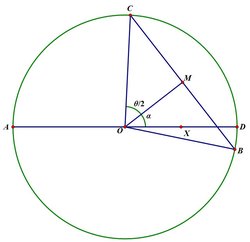
The polar coordinates of the midpoint M of B C are ( s , α ) , where s = 3 cos 2 1 θ , where θ is the non-reflex angle ∠ B O C . Since θ and α are essentially the difference and average of the two polar angles of B and C , the random variables θ and α are independent. Note that θ is uniformly distributed over ( 0 , π ) , while α is uniformly distributed over ( − π , π ) . Thus P [ s ≤ u ] = P [ cos 2 1 θ ≤ 3 1 u ] = 1 − π 2 cos − 1 3 1 u 0 ≤ u ≤ 3 and hence s has the probability distribution function f s ( u ) = π 9 − u 2 2 0 ≤ u ≤ 3 Note that s and α are independent. The centroid G of the triangle A B C is obtained by enlarging M by a factor of 3 2 through the point A . Suppose that r is the distance O G of the centroid from the centre of the circle. Then r ≤ u precisely when G lies in the circle, centre O of radius u , and this occurs precisely when M lies in the circle C u of centre X and radius 2 3 u . Thus the probability that r ≤ u is the probability that M lies in the intersection of C u and the original circle.
When 0 < u < 1 the circle C u lies entirely inside the original circle, and C u can be described in polar coordinates as follows: 2 3 ( 1 − u ) ≤ s ≤ 2 3 ( 1 + u ) ∣ α ∣ ≤ cos − 1 ( 1 2 s 4 s 2 + 9 − 9 u 2 ) Thus P [ r ≤ u ] = π 2 2 ∫ 2 3 ( 1 − u ) 2 3 ( 1 + u ) cos − 1 ( 1 2 s 4 s 2 + 9 − 9 u 2 ) 9 − s 2 d s = π 2 2 ∫ 1 − u 1 + u cos − 1 ( 2 v v 2 + 1 − u 2 ) 4 − v 2 d v 0 < u < 1
When 1 < u < 3 the situation is more complicated, since the circle C u contains O and extends beyond the original circle. For us to have r ≤ u , we must have either s < 2 3 ( u − 1 ) or else 2 3 ( u − 1 ) < s < 3 and ∣ α ∣ ≤ cos − 1 ( 1 2 s 4 s 2 + 9 − 9 u 2 ) .
Thus P [ r ≤ u ] = π 2 ∫ 0 2 3 ( u − 1 ) 9 − v 2 d v + π 2 2 ∫ 2 3 ( u − 1 ) 3 cos − 1 ( 1 2 s 4 s 2 + 9 − 9 u 2 ) 9 − s 2 d s = π 2 sin − 1 2 u − 1 + π 2 2 ∫ u − 1 2 cos − 1 ( 2 v v 2 + 1 − u 2 ) 4 − v 2 d v 1 < u < 3 Thus we have a piecewise definition for F r ( u ) = P [ r ≤ u ] , which does not seem likely to be something we can evaluate exactly! Here is a numerical plot of F r .
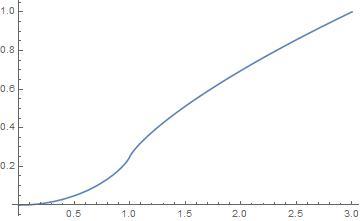
Note that F ( 1 ) = 4 1 , as expected.
@Calvin Lin – I can obtain an expression for the CDF f ( r ) , at least for 0 < r < 1 . It is in the form of a complicated integral. The form of f ( r ) changes for 1 < r < 3 , but can still be evaluated numerically. It will take some typing out, so you will need to wait a bit. From what I can tell, the cdf is not differentiable at r = 1 .
If O , G , H are the outcentre, centroid and orthocentre of the triangle, then O H = 3 O G , and so the required condition is the same as asking that O H < 3 r , or that the orthocentre lies inside the outcircle of the triangle.
Now the orthocentre of a triangle lies on the outcircle precisely when the triangle is right-angled, and lies outside the outcircle when the triangle is obtuse-angled. Thus we are asking for the probability that the triangle is acute-angled.
Without loss of generality, one point A on the triangle can be assumed to be fixed. The second point B will form an angle θ = ∠ A O B , where 0 ≤ θ ≤ π , and θ is uniformly distributed over [ 0 , π ] . The triangle A B C will be acute-angled precisely when C lies on the arc of the circumcircle which is diametrically opposite the minor arc A B . This is an arc subtending the same angle θ at the centre of the circle. Thus the probability that the triangle is acute-angled is π 1 ∫ 0 π 2 π θ d θ = 4 1 making the answer 0 . 2 5 .