150 Follower Problem!
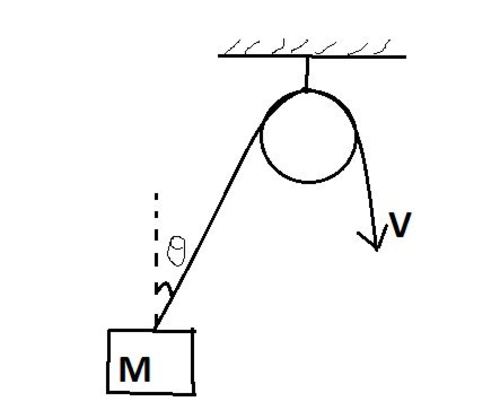 In the following set up the rope is pulled with a Velocity
V
and the block of mass
M
starts moving horizontally initially and then moves up. Let at
t
=
0
the block make an angle of
ϕ
with the vertical. At
t
=
t
1
the block makes an angle of
θ
with the vertical.Given it doesn't move upwards till
t
1
find the horizontal velocity at
t
=
t
1
.
In the following set up the rope is pulled with a Velocity
V
and the block of mass
M
starts moving horizontally initially and then moves up. Let at
t
=
0
the block make an angle of
ϕ
with the vertical. At
t
=
t
1
the block makes an angle of
θ
with the vertical.Given it doesn't move upwards till
t
1
find the horizontal velocity at
t
=
t
1
.
Details and Assumptions :
-
V = 1 5 0 m/s
-
θ = 3 0 ∘
The answer is 300.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Could you tell me what is the virtual work method. I solved using components.
Log in to reply
I don't know its proof but for a closed system ∑ T . V = 0 always holds and ∑ T . A = 0 also holds but there are some situations in which the latter one does not holds. Watch this video to know more about this.
Log in to reply
Is T over here Tension.
Basic Consideration : Velocity along the string is the same everywhere.
Let the required horizontal velocity be V x , then
V x cos 6 0 ∘ = V , or V x = 3 0 0 m/s .
Considering H as the height of pulley, R the lenght of the rope and x the distance of the block to the vertical of the pulley, being R=R(t) , x=x(t) and H equal a constant. Now we can write by Phytagoras
R 2 = H 2 + x 2 so derivating by t and after simplification we get
R d t d R = x d t d x
Since x R = cos θ 1
By substitution of given value we get the velocity of the block is twice of the rope
T h i s f i g u r e s h o w s t h e p o s i t i o n o f t h e b l o c k a f t e r a n e g l e g i b l e t i m e Δ . S i n c e t h e v e l o c i t y o f t h e r o p e i s V , i t s l e n g t h o n t h e l e f t s i d e o f t h e p u l l e y c h a n g e s b y Δ . V i n Δ t i m e . S o A B = Δ . V ( 1 ) A C i s t h e d i s p l a c e m e n t c o v e r e d i n Δ t i m e b y t h e b l o c k . S o , A C = Δ . U ( W h e r e U i s t h e v e l o c i t y o f t h e b l o c k ) ( 2 ) B y s i m p l e t r i g o w e c a n s e e t h a t A C = A B csc θ ( 3 ) U s i n g ( 1 ) , ( 2 ) a n d ( 3 ) , w e g e t Δ . U = Δ . V csc θ S o U = V csc θ S o U = 1 5 0 × 2 = 3 0 0
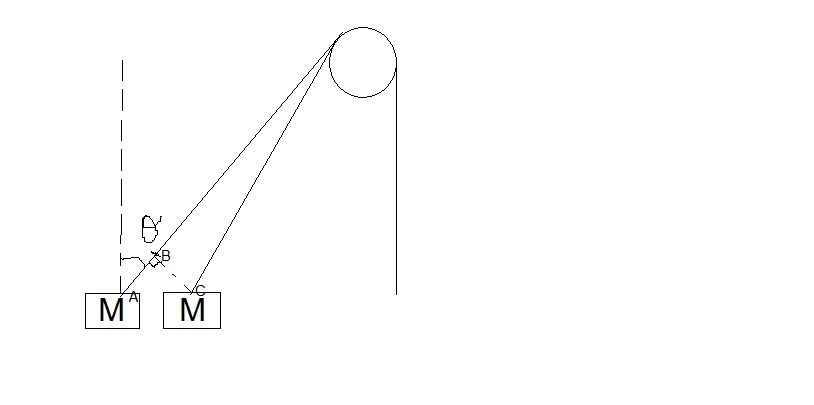
How do you know AB ⊥ BC. Well you are assuming AB = Δ V. So why perpendicular ?
Log in to reply
Let D be the point of intersection of rope and pulley
We assume that the triangle BCD is isosceles. And angle BDC is 0 because the time is negligible, so ABC=BCD=90
Check out my new wiki Tribonacci sequence
Simply use virtual work method.
For any close system ∑ T . V = 0
Let the velocity of the block be v 0 (in horizontal direction).
So − T V + T v 0 c o s ( 9 0 − θ ) = 0
So v 0 = 3 0 0 m / s