1729 is interesting!
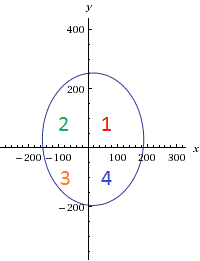 The above diagram shows an ellipse
(
E
)
:
1
7
(
x
−
1
7
)
2
+
2
9
(
y
−
2
9
)
2
=
1
7
2
9
Suppose
S
1
,
S
2
,
S
3
and
S
4
represent the area of 1, 2, 3 and 4 marked on the diagram. Determine the value of
M
=
S
1
+
S
3
−
(
S
2
+
S
4
)
.
The above diagram shows an ellipse
(
E
)
:
1
7
(
x
−
1
7
)
2
+
2
9
(
y
−
2
9
)
2
=
1
7
2
9
Suppose
S
1
,
S
2
,
S
3
and
S
4
represent the area of 1, 2, 3 and 4 marked on the diagram. Determine the value of
M
=
S
1
+
S
3
−
(
S
2
+
S
4
)
.
The answer is 1972.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Amazing problem! The solution was very nice too; thank you for making this.
Very nice solution and surprising and interesting answer! Happy birthday to your mom by the way!
Log in to reply
Thank you!
Log in to reply
I think you should include 17,29,19,7 and 2 in your next lottery selections. They are all primes too. I love spooky stuff like this !!
Is the fact that 1972 is a permutation of the digits of the Hardy–Ramanujan number 1729 by design ? This problem is Fantastic !! Such a clever solution as well !!
Log in to reply
Yes, I realized this interesting feature by chance but waited for long to post it. Actually the answer is coincident and has nothing to do with 1729.
Log in to reply
Awesome. Actually I did this problem by numerically slicing the four regions and finding values for S1=39347 , S2=30760 , S3=21886 , S4=28501 .... then 61233-59261=1972 ! I knew my whole number approximations would be off by a tiny bit; however, when 1972 popped out I had faith the universe was smiling on me and I should type in that answer ! I like your solution so much better. The strategy is firmly locked into my mathematical tool box. Thank you for posting this problem and giving me an evening of absolute bliss !!
Log in to reply
@Bob Kadylo – You're welcome! It's so normal to resort to calculus when it comes to these kinds of problems I guess. But can you show me how could you do this with calculus?
Log in to reply
@Leah Smith – Your method is much better and more accurate. What I did was look at each of the 4 regions separately and then by using numerical integration (Riemann Sums) with 2000 slices - I got approximations for the areas between the equation of the ellipse and the x-axis (4 times). In quadrants #1 and #2, my values are a little bit low because I missed thin slices on the far left and far right where the ellipse went a bit left and right of the x-intercepts. This happened because the centre had been shifted. Luckily the way you asked for the answer, M, made the errors cancel out - the amount I should have added to S1 would have been subtracted off by the amount I should have added to S2. Now you understand my surprise that I got the problem correct. My objective on Brilliant is to learn the more elegant ways of solving problems and use the numerical approximation techniques less and less.
Log in to reply
@Bob Kadylo – Wow that requires a lot of hard work, bravos to you! In mathematics even a small margin can make a big consequence! Luckily this problem is at least somehow extraordinary so you did spot the oddity! May I ask are you a lecturer at the university?
Log in to reply
@Leah Smith – I am a retired high school teacher who graduated from the UofA in 1974. My addiction to Brilliant comes at the perfect time in my life.
Log in to reply
@Bob Kadylo – Well I'm studying at University of Arizona in Tucson. My addiction to brilliant was 4 months ago but now I rarely use it but I still enjoy raking hard problems!
First we have to prove that I ( 1 7 ; 2 9 ) is the ellipse center. Suppose P ( x 0 ; y 0 ) be a point on the ellipse ( E ) . That means: 1 7 ( x 0 − 1 7 ) 2 + 2 9 ( y 0 − 2 9 ) 2 = 1 7 2 9 ⟹ 1 7 ( ( 3 4 − x 0 ) − 1 7 ) 2 + 2 9 ( ( 5 8 − y 0 ) − 2 9 ) 2 = 1 7 2 9 ⟹ P ′ ( 3 4 − x 0 ; 5 8 − y 0 ) is also on E . Futhermore, I P = ( x 0 − 1 7 ; y 0 − 2 9 ) = − ( 1 7 − x 0 ; 2 9 − y 0 ) = − I P ′ . Therefore, I is the center of ( E ) .
Now, as the center is found, we have another diagram of ( E ) .
Suppose S is the area of ( E ) , A + B + C + D + E is the area of the colored regions. Based on the graph, we have:
S 1 = 4 S + A + C + E
S 2 = 4 S − A + B
S 3 = 4 S − B − C − D
S 4 = 4 S − E + D
⟹ M = S 1 + S 3 − S 2 − S 4 = 4 S + A + C + E + 4 S − B − C − D − 4 S + A − B − 4 S + E − D = 2 A + 2 E − 2 B − 2 D
A = C + D ; E = B + C so M = 4 C = 4 . 1 7 . 2 9 = 1 9 7 2 .
1972 is my mom's birthyear and today is her birthday. This problem is dedicated to her.