Can You Make This Equation True?
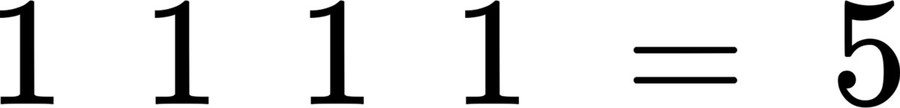
Do there exist operations that can be performed to make this equation true?
Note: Any operations can be used, so get creative!
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
192 solutions
Discussions for this problem are now closed
(1+1)square+1/1= 5
this is what i came up with......why cant u square it says to use ANY operations....?
I don't think this is allowed because of the square uses 2.
Wow,you can really think broo
ah ha i understand why now!
@John Turgeon – I think you give up too easily. The 2 is an operator I'd say. For square root could we use ^0.5 instead of the sqrt or the square root "bracket". If I were programming the expression in many computer languages Sqr( ) would square an expression. I chose (1+1)!+1+1.
@Robert Lucas – That makes 4
@Tom Mcconnell – (1+1)! = 2! = 2+1 = 3 Then add 1+1 to that and it equals 5
@Adam Buckley – No 2! = 2*1 not 2+1
you can't square, that's (1+1)^2 + 1/1 no 2s only 1s
Not if you write it as "sq.", which many do. That's just as valid as using ! as factorial.
@R. Chase Razabdouski – sq is a binary opn
@Mohd Wasih – multiplication is a binary operation, but if you define squaring as multiplying the same number with itself. you don't need two numbers to square
((1+1)^1)+1
@Pinky Stiles – ((1+1)^1)+1 = (2^1)+1 = 2+1 = 3 And 3 is not 5
@Boyce Towell – I think "^" is a square she means :3
@Luwi Fernandez – If so she would only have three "1"s, not the four in the problem.
Squaring isn't an operation, but you can do (1+1)^(1+1)+1=5
That's using five 1s
i think we should use only signs, not numbers. square makes solution wrong.
I think you can't use squares or powers because that's writing numbers
This is largely a matter of notation. Squaring a value could be considered as having a single operand whereas if it is considered more generically as raising to a power then the 2 is needed as an operand. The problem is that the notation to be used is not defined.
1/.1/(1+1) is how i did it
A decimal point isn't an operator...
Decimal point is not an mathematical operator; you changed the number.
Excellent!
That's exactly how I did it
How about this??
(11-1)>>1 =5..Computer Science people will know!!
[11/(1+1)]=5, where [] is the greatest integer function
@Sachin Sharma – Wouldn't that yield a 6?
@Zoran Lalvani – How???
[11/(1+1)] = [5.5] = 5, since 5 is the greatest integer which is less than or equals to 5.5
@Sachin Sharma – ......... whaaattt
@Sachin Sharma – You mean the floor function.
@Sachin Sharma – We need operation like ! Not functions
@Oussama Rhelimi – An operator is an abstract thingy that takes another thingy as input and creates a third thingy as output!
a binary o p e r a t i o n ∗ on a set S is usually defined as f u n c t i o n ∗ : S × S → S
where for simplicity we write a ∗ b instead of ∗ ( a , b ) .
Some examples of operators:
1) Laplace, Fourier, and Hilbert transforms. These operators map functions into functions
2) derivatives and integrals. Ditto
3) differential and partial differential equations: the input function is mapped through the operator into an output function
4) Eigen-analysis is an operator mapping matrices into eigenvectors and eigenvalues
5) All matrix decompositions are operators, QR, tridiagonalization etc.
Note that things like ÷ is not an operator because the domain of ÷ is not R 2 .
@Sachin Sharma – What about accuracy?
@Zoran Lalvani – That would be 5.5
@Zoran Lalvani – No, it's greatest integer less than or equal to whatever is in the brackets.
Or:
1 1 + 1 + 1 = 5
Where it is read in Base2 before the "=" and is read in Base10 after
@Kyle Fairns – I guess I would suggest just writing 11+1+1 = 101 then. I dunno, the problem used a 5 as a value so should make it at least a base 6 problem. ;)
Indeed — my solution was a variant of your bit-shifting, namely ((1<<1)<<1)+1=4+1=5. Or ((1<<1)<<1)|1=4|1=5 if you truly want to geek out.
@Bert Sierra – I had a similar solution ((1+1)<<1)+1
Well Done man
Correct me if I'm wrong, but I don't think combining 1 and 1 to make 11 is a permitted step. Good idea though!!
Nice!
>> is binary right shift in C style programming languages which is equivalent to integer division by 2.
Yeah bro..!!
A little shifty, but nice.
plz explain how did u do it
11+1+1=101 (using binary operation)=5
Did that way too.
Yes, that's exactly how i thought !
yep! that's it!
i think the use of arrays where the starting point is 0 can solve this..
Change the lhs to base-4:
11 in base-4 is 5...
Sqrt(11)*Sqrt(11) = 11 = 5 ( base 10)
I feel like its not okay to use sqrt since its translated into ^1/2. One other person couldn't use ^2 as an operation
(1+1)^2 + (1 x 1)
Very creative !
(1/.1)/(1+1)=5
I cannot agree because 0.1 is not 1.
(1+1)^2X1+1 = 5
i don't think using another digit is permitted
This isn't another digit it is square of (1+1)
@Resat Uzmen – you are using the digit '2' as an exponent which is not permitted; we can only use 4 digits & they are all ones
same answer... :)
Are brckets included in operations?
I did not like this question. Why is a factorial more valid than a ^2? If anything ^2 is more valid, because I am not actually using the number two. I am only denoting that I am multiplying the number by itself once. If I go ^3, then I am multiplying the number by itself twice, and so on.
A factorial is just a way of bringing other numbers into the equation while pretending that you are not bringing other numbers into the equation. If you use the factorial function, you have actually used other numbers than the numbers provided. It is implicit in the factorial function that you are using other numbers than the number itself.
When you square something you are still only using the numbers give, you just use a 2 or 3 or 4 to indicate how many times the self multiplication function is applied.
You're assuming that ^2 is a basic operation which is not. It's the most common number for that operation.
^2 is just the most common exponential there is I guess, but that does not mean every exponential out there ends with a 2. You can do ^3, ^4, ^x...
Point is that's just like multiplying something by 2 and saying your not using the number 2 when you actually are...
I was in the process of explaining why I disagree with being allowed to use exponents, however after giving it more thought, I think it is allowed. Raising something to a power is simply multiplying it by itself several times, and exponents are operation, I mean Pemdas, so no rule is broken, right?
that's exactly i came up with. Similar to this can 3 0's ever form a 6? (an easy self devised question)
Am I wrong ? 1. (.1/1 + .1)^-1 = 5 2. | sqrt(11) | + 1 + 1 = 5 3. (smallest integer function(sqrt(11)) + 1)/1 = 5
(((1+1)^2)+1)/1
Why not just derive them?
(1+1)^2×1+1
I think this should work... because it doesn't have any extra #s
What does this ! mark mean???
it's called factorial. which means 3! = 1x2x3 =6, 5! = 1x2x3x4x5 like wise n! = 1x2x3x....(n-1)xn
thank you very much ^_^
https://en.wikipedia.org/wiki/Factorial
thanx a lot
! stands for factorial
Factorial (1+1+1)!-1=5
conguralations
1+1=2 2^2=4 4/1=4 4+1=5
I disagree with this solution. The factorial operation is shortened as a ! but in reality is several numbers, none of which were listed in the numbers being used. In addition, the single spacing between each number 1 implies their is ONE operation between every number, which is obviously not the case in the solution. This is misleading and does not fall in line with operator search rules.
If you think the use of factorial is cheating, then you may as well disqualify the use of exponentiation, and multiplication, since exponentiation is a series of multiplications, and multiplication is a series of additions.
Oh wait a minute, that doesn't sound like a very good idea...
Finally someone who actually understands what is going on, so many uneducated people in here thinking there are mathematical geniuses
first get this - an Operator is a FUNCTION from a predefined set to another set.
So first off, where in the question does it say that you can't use more than one operation in between spaces, oh wait never mind, I can clearly see you have just made it up your head, how ignorantly stupid of you
Wow, there's really no need to be mean. People are here to learn and if you feel the need to insult people that know less about mathematics than you do then you are truly the ignorant one.
How dear.....give me detail
Factorial is not an operator. It is a representation of product of natural numbers less than and equal to itself.
I still don't understand...😅 isn't that 2 ???
Or (1+1)!+1+1
That is equal to four.
(1+1)^2+(1+1)^0 or better than this => (1+1)^(1+1)+0^0
0^0 is nothing. It is an indeterminate form.
not by convention
You are adding a digit "2" and "0" though? Should only be using the 4 provided "1's"
So we cant use ! cuz it adds other numbers to the problem. Factorial isnt an operator, its just a simplified form to write.
@Rafael Vale de Sousa – It is a function. Functions are a name for binary operators. Factorial is a valid form here, but the people trying to use '^2' are using an invalid form. Squaring is not an operation. Exponentiation is the operation. But it's a vaguely phrased question, regardless.
@Rafael Vale de Sousa – Let U, V be two vector spaces. Any mapping from U to V is called an operator. Therefore, using factorial maps a vector value to another vector value by carrying out a series of multiplications does it not? (That is rhetorical as obviously that is the case) Therefore, it is quite blatantly true that factorial is an operator. You could use your poor argument to say multiplication isn't an operation as A multiplied by B, is just a simplified version of adding B numbers of A together, so you could say multiplication is a simplified way of addition, does that stop being an operator, obviously not, get educated
@Harry Williams – Despite your useless explanation with vectors, that could trick people without knowledge, for math ! continues to be a function, not operator, im not your teacher nor you are mine, its my opinion that as yours wont make any change to the world but arrogance and intolerance will ;)
my solution was very easy 1+(1+1)2 / 1 = 5
I don't think we can put the power two....coz its not an operation
thats square
Where did that 2 come from?
Mr. Jim that means square
@Jhean Nheaj – You can use exponent function but not 2 as an exponent unless it's obtained by operations on the four 1s. Otherwise what's the problem in multiplying with 2 or any number obtained from your head?
Why not (1+1)*2+1?
Wow, why didn't I think about changing the problem?
I don't think u can use 2
That won't work because 2 is not part of the problem
cuz you are using three 1's !
Oh... I think it was like 3 AM when I wrote that... Just now I saw instantly what the issue was haha
(1+1)² + 1 x 1 = 5
0.1 is not the same as 1
how can 1+1+1+1=5? it is = to 4
a bit misleading perhaps. if any operation is allowed, I could simply define an operation, say &, such that 1&1 = 5, and then add and subtract the two other ones....
Then you should be able to define the operation on all real numbers successfully without having to define it for each number explicitly. Get the point?
Easy: A&B&C&D = 5 if A = B = C = D; else, A&B&C&D = 0
+1 Never thought of that :-D Sorry
No, because what you have done there is called, 'creating a function' and that is basically the one very clearly defined thing that is not an operator, functions are completely different and are usually made up of a lot of operators, good try though with your arrogant conclusion, shame you are ignorantly stupid and uneducated
You cannot use extra digits.. :/
squaring is an operation, not a digit.
Yes it is. Raising it to a power an operation (^) but adding a digit to decide which power it's raised to, is!
Squaring is not an operation...its transformation...u're transforming the number to its square
@Kuduvan Vaishnav – Let U, V be two vector spaces. Any mapping from U to V is called an operator. Therefore, using factorial maps a vector value to another vector, or 'translates' it, still making it an operator clearly. The only problem is that the operator is the '^' and the number placed afterwards is not included as the operator, so you can't just decide you want to add a two and call it squared, and that making it and operator, that is like using a function that inverts a value, then calling it the 'inverse' and deciding as you gave it a nice name it now becomes an operation, it clearly doesn't
How about: − 1 ( 1 + 1 ) + 1 ,
where − 1 stands for the inverse of the square root function, i.e. the square :)
This is incorrect, you can't just use the square root operator without giving it a power, the power here for the square root is 2 which you haven't stated but just merely assumed, you can't just include a 2 and keep it discrete in order to solve the equation, you must state all numbers used, which you haven't, and if you did you would see that the root operator is of power 2 meaning not all '1's have been used
@Harry Williams – The square root x is the same as the x 1 / 2 but that does not make my approach invalid... Moreover, it is customary to use f − 1 for the inverse of a function f , e.g. sin − 1 x is the inverse of the sine function. So I don't really see what the problem is. And you will notice that I used the numeral "1" four times.
Maybe you don't like create solutions and I am willing to admit that this one is contrived, but isn't that the fun of it? The problem said "so get creative"-- and I did!
That was not a rule in the given problem. Plus it said to be creative.
My bad. I did not read the note that says " Any operations can be used". And yes, squaring is an operation .
Really, then i can double any number and say doubling or multiplying by two is an operation just like raising to the power 2.
@Kuduvan Vaishnav – Someone whom understands maths, this is a breathe of fresh air😂
Someone whom doesn't know how to use 'whom'
Well done gautam. Keep it up
(1+1+1)! - 1 = 3! - 1 = 1x2x3 - 1 =6 - 1 =5
[11/(1+1)] Where [x] is integral part of x.
(1<<(1+1))+1 Bitwise left shift is beautiful operation.
1111≠5 [ps. dont complicate things.. read the question carefully]
The question says you are supposed to make the EQUAtion true. An equation must have an equal sign. You should read the question more carefully. '-'
its not so much complicated. its very simple. just add one diagonal tally mark
Haha.....everyone doesn't like the diagonal line through the equal sign....so make it a diagonal tally.
That yields 2, though.
I also thought of this 👍🏻
you should use prefix operator instead of post fix (ie ++1 in place of 1++)
Let *: Int -> Int be defined as the constant operation: a * b = 5. for all integers.
Ceiling(Sqrt(11 x (1 + 1))) or Replace Ceiling with Round.
Or Floor(Sqrt(Sqrt(1111))
Or this. Ceiling(Arctan(Sqrt(Cot(Sin(Cos(11!))) + Cos(11 ∘ )))). The first trig argument is in radian, the second is in degree. I propose some change in this problem. Let's find the maximum amount of operations without using programming LOL.
I took it as tally marks, and closed the gate (put in a slash to make it 5)
In base 2,
11+1+1=111
Wich represents 5 in base 10.
Best is to use factorial for sum of first three one and then subtract them
(1+1+1)!-1.
(3)!-1
6-1=5. ... Hence,,, Proved
1-1+1+1=5 upside down of reads 2=1+1+1-1
Ackermann(1,1+1)+1 OR 1×Ackermann(1+1,1)
This is the only ideal solutionsolution
Define five(x)=5 and zero(x)=0. five(1)+zero(1+1+1)=5
\frac {d(1+1+1+1)}{dx} = \frac {d(5)}{dx}
Yes, that evaluates to 5. However, you have also used a 2 , which is not allowed!
.1^(- 1)/(1+1)
(1+1+1)!-1=6-1=5
(1+1+1+1)^0 = 5^0
(1+1)^2+1×1=5 I guess, looking at others comments I wasn't allowed to square
(1-1)/(1-1) Could be basically anything, including 5
This is the most genius of all the solutions! :-) although sadly, it doesn't work. But screw the rules - I still think is the most genius in a diabolically creative way. well done!
You can use any one e.g. PEMDAS rules, FOIL. My friend use arc cosec of something to solve but it is too complicated. I use very simple math.
All the top poi TX on the "ones" are equal to all the points of the five.
ln 1 + 1 − 1 + i = 1 ∑ 5 1 = 5
My solutions use only 3 ones.
⌈ . 1 1 ⌉ + 1 = 5 ,
⌊ . 1 1 ! ⌋ − 1 = 5
(1×1)×1×1=5, 1×1=5, 1÷1=5÷1, 1=5,
0111- 0010 = 0101 in binary 7 -2 =5 in Base 10
Just use the 'Not Equal' sign :p
\left \lfloor{11÷(1+1)}\right \rfloor = 5
f(1)+ 1 + 1 + 1 =5 where f(x)= x+1
11/11=5 5*11 is 55. 55/11 is 5
((1+1)^-1) exp 1 = 5. Isn't that right?
This expression doesn't even result on 5. 1 + 1 = 2, 2² = 4, 4 * 1 * 1=4. And you shouldn't use a number 2
I just said 1+1+1+1 does not equal 5 you know. The equal with forward slash through it.
(1+1+1)! - 1= 5. I figured this out on my own, but saw the answer posted before 1 posted mine. Is there a way we can post our results before seeing anyone else's?
Could ((1+1)^(1+1))+1 be 5. I think it could
It took no time to get to the solution as ( 1 + 1 + 1 ) ! − 1 = 5
Note: This is not a solution
1 + 1 + 1 + 1 = 5
In python
x=sqrt(11)+(1+1)
print(int(x))
5
(1-1)/(1-1)=0/0=all real numbers.
Why it won't work (1/.1)/(1+1)
Abusing the C/C++/Java programming language:
(++1)+1+1+1=5
floor[11/(1+1)] = floor(11/2) = floor(5.5) = 5
1 (1-1) 1 = 101 = 5 in binary
1 = 1/2 +1/2
(1/1/2)+(1/1/2)+1
2+2+1=5
(1<<(1<<1)) | 1 = 0b00001001= 0x05
1+1+(11base2)=5 ;whereby 11base2 is 3 XD
Yes, it's not that hard: (1+1+1)!-1=5
{1(1+1)}×1 where {} is fraction part.
1 + 1 + 1 +1 +1 - 1 = 5 1 + 1 + 1 × (1 + 1) - 1 = 5 3 × 2 - 1 = 5 6 - 1 = 5 5 = 5 hence proved 😊
(1+1)×(1+1)+1=5
(1+1)^(1+1)+1=5
(1+1+1)! - 1 ==> 3! - 1 ==> 1 2 3 - 1 ==> 6-1=5 ==> 5=5
The best solution is 1/.1/(1+1)
Of course there is. Let's define ⊗ such that n ⊗ m = n + m + 1 . Then ( 1 + 1 + 1 ) ⊗ 1 = 3 + 1 + 1 = 5 .
How about (1+1)^2 + (1+1)^0 = 5?
(1+1)x2+1=5 (1+1)=2x2=4+1=5
[1+1+1]!-1=5 the only solution left.
Take this new challenge
1*1= 1
2*2=2
3*3=3
4*4=4
5*5=5
6*6=6
7*7=7
8*8=8
9*9=9
Any operation can be uses except cube root. If finally not possible then use cube root.
In excel if you have four cells with 1.25 in them,but you have the decimal point set to whole numbers each cell will show 1, but when you sum the answer is 5.
antilog(1)*1/(1+1) = 5
using this solution I only need three 1's
It strikes me that the (1+1+1)! – 1 = 5 solution is the most elegant and mathematical. [from Abdur Rehman Zahid]
I started out as a C programmer, so to me my bag of operators would include bitwise operators in addition to the arithmetic operators, in which case there are a couple of ways to make the equation true:
((1<<1)<<1)+1 = 4+1 = 5 ((1<<1)<<1)|1 = 4 | 1 = 5
…but then if you allow for the expressiveness of C, there is also the trivial case below:
!(1+1+1+1 == 5)
which is most certainly true and would also lead to a large number of trivial variants in which you flip false to true at the end.
You run into a bit of a semantic problem because it’s not clear if the ‘operations’ should be applied to the 1s only, or could be applied to the equation as a whole. Also, to be a bit more picky, the word ‘operation’ isn’t quite ‘operator’, which might be a language issue — so presumably if a function could be considered an operation you could solve it trivially this way:
Given: f(x) = 5
Then f(1+1+1+1) = 5. QED.
[short answer — YES… there are several combinations of ‘operations’ which will work. The question is somewhat “Internetty” and so by exploiting vagueness in the question you can most certainly find a solution.]
[ ( 1 + 1 ) squared + 1 ] x 1 = 5 Sorry I don't know how to type an exponent on this keyboard :) I believe squaring something is an operation. What are people's thoughts?
write it on binaries (11)=3+1+1=5
How about something like this?
( 1 + 1 ) 2 + ( 1 + 1 ) 0 = 5
That's exactly what I got
Make up an operator that takes 4 1's and returns five. The question doesn't state that you must use standard arithmetic operators. Given this, the answer is obviously yes. Quite Easilly Done.
I have no idea if this is right or cheating or not but me and my classmates thought of this way 1 1 1 1 = 5 You take the first 1 witch is equal to 0,5 and 0,5 then you divide the second 1 with 0.5 ( 1/0.5) = 2 then you do the same with the second 1 (1/0.5) = 2 and add the remaining 1 So (1/0.5) + (1/0.5) + 1 = 5
Or the easier sulotion would be (1+1)^2 x 1 + 1 = 5 But we thought that was alittle too easy.
(1+1)^2 + (1*1) =2^2 + 1 =4+1 =5
1x10^1 (ie 1e10)=10 and so 1e1/(1+1)
Not completely valid because of the exponents...But I still had fun coming up with it...
(1+1)^(2)+(((1+1)^(2))^(0))=5
That's pretty much what I got, (1+1)^2 + (1+1)^0, not sure if those operations are allowed though
(1+1)2 (2 being squared) +1x1
Ha-ha I thought it was asking for something like 1111 - 1106= 5
. 1 + . 1 1 ⋅ 1
⌊ 1 + 1 1 + 1 ⌋ = 5 . Here, 1 1 is of course the letter π . ⌊ 1 1 1 1 ⌋ = 5 .
∣ 1 + i + 1 ∣ 1 + 1 = 5 .
1 1 + ϕ ( ϕ ( 1 1 ) ) = 5 . Here, ϕ ( n ) is the totient function.
[ π 1 + 1 ] = 5 . The [ ] may be viewed as variations on the digit 1.
Add first three ones and take the factorial of 3 which will equal to 6 and subtract remaining 1 from it which will give 5
Lets assume these numbers are in base 2 not base 10 hence (1+1)+1+1=5
(1+1)base2 + (1)base2 + (1)base2
(1+ 1) squared, + 1, / 1 = 5
(1exp1)/(1+1) = (10/2) = 5
(Log(1+1+1+1))/ Log(x) = 5, does it works?
equal anyone side with other like 1+1+1+1= 5-1 bring negative one on the left side 1+1+1+1+1= 5 BE CREATIVE that's what the question says
11 (base ten) - 11 (base five) = 5 (base ten)
Relevant wiki: Arithmetic Puzzles - Operator Search
In this operator search puzzle, the big hint is the exclamation mark at the end of the note! It's suggesting that we use factorial! ( 1 + 1 + 1 ) ! − 1 = 5