Hit The Right Angle
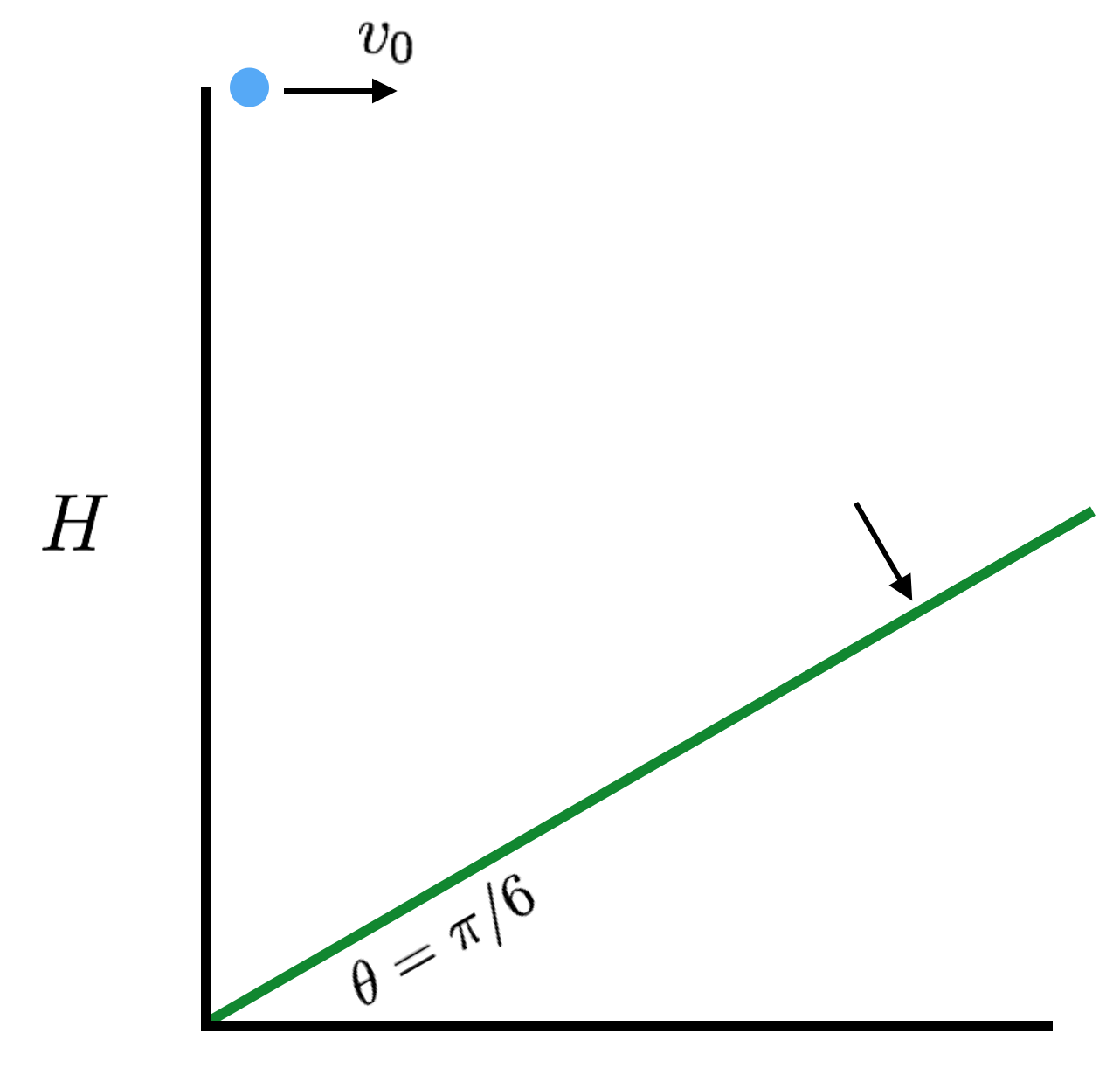
A particle is projected with velocity v 0 horizontally from a height H over a hill, and strikes the hill perpendicularly.
Find 2 g H / v 0 2
Assume the hill rises linearly from the origin at an angle θ = 6 π = 3 0 ∘ .
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
A unique and fabulous approach
This can be easily generalized. Doing that we get :-
v 0 = 2 + cot 2 θ 2 g h
Absolutely brilliant and unique approach!!
Same method...
That's Good! My main motive to post this question here was to know different methods to solve this problem, as the one I used is a bit time consuming. Sargam Yadav posted one good solution.
@Vatsalya Tandon try my problem That is close 2 , it also needs similar approach
Well this question is correct I solved it on my own... It has given all the required details...
how did you upload that picture ? because i used the same way of heights and equation of motion and i am getting the answer as 4 root 3 i would like you to check it.
Log in to reply
I use desktop. First open solutions. In that you have option to add picture. But if you are using an app then I don't know.
Log in to reply
i found a way to upload my solution you can go here : https://brilliant.org/problems/solve-it-17/ solve the problem and i have added my solution there . please check and tell me my mistake , i'll be glad
Well anyways just tell whats the difference between your solution and my solution. I mean time or v'.
Well everyone just try to solve this question https://brilliant.org/problems/confusing-sometimes/ posted by me
Suppose the particle covered distance 's' vertically before striking the plank. Then 2gs=(√3 V°)^2. AS velocity in vertical direction at the time of striking the plank is √3V° as velocity at time of striking made angle 30° with vertical and 60° with horizontal by geometry. Therefore horizontal distance travelled by particle before striking is V°^2√3/g. s=3V°^2/2g. H—s = V°^2/g by trignometry. Therefore H = 5V°^2/2g. So, 2gH/ V°^2 = (5.).
Did the same!!
I also did the same.
i did the same way too
Can anyone tell me how to attach a photo with a soln..
Log in to reply
Hi Sargam. Click "Edit" on your solution. That will bring up some formatting options like this:
 If you click the third button from the left, it will bring up a upload menu that lets you upload an image. It will then insert the link to your image directly into your solution which you can then move around as you wish.
If you click the third button from the left, it will bring up a upload menu that lets you upload an image. It will then insert the link to your image directly into your solution which you can then move around as you wish.
Log in to reply
But there are no formatting options coming...
Log in to reply
@Sargam Yadav – Can you be more descriptive about what happens when you click edit?
Log in to reply
@Josh Silverman – When i click edit — (1)sargam yadav july 13,2016 (2)Relevent wiki (optional)[start typing to select a wiki] (3) [body of solution] (4) formatting guide (5) submit (6) cancel, preview..
Log in to reply
@Sargam Yadav – Are you using a phone or a computer?
Log in to reply
@Josh Silverman – I am using a phone...
Log in to reply
@Sargam Yadav – Ah, that explains it. Unfortunately, there is currently no photo upload functionality when entering a solution on the mobile app.
Log in to reply
@Josh Silverman – no,there is. i read a same que on brilliant site which i asked. the ans was written that one have to first upload the photo to the apps such as flickr or some sites that they had mentioned(i do not remember) and then copy the image link to where you have to upload the photo. i tried using the app flickr ,then copy and paste but i failed to upload that photo at brilliant.......do not know what to do..... sorry for taking your so much precious time..... but its okay if there is not a way.... thank you so much......
Log in to reply
@Sargam Yadav – That is true, you can upload it elsewhere and then link it in. Is the phone the only way you have to use Brilliant?
But there are no formatting options coming..
The velocity of the projectile over time is given by v = ⟨ v 0 , − g t ⟩ and the direction of the hill is given by h = ⟨ cos π / 6 , sin π / 6 ⟩ . The projectile collides with the hill perpendicularly if the dot product of its velocity with the direction of the hill is zero. This leads us to the time of collision with the wall a la v ⋅ h = 0 = v 0 cos π / 6 − g t sin π / 6 → t = g v 0 cot π / 6 The height of the cliff is then the height the projectile falls before colliding with the hill h 1 , plus the height of the hill at which it hits h 2 . By trigonometry, we see that tan π / 6 = h 2 / r x where r x is the x position at which it hits the hill. Therefore, the total height H = h 1 + h 2 is given by H = r x v 0 t tan π / 6 + 2 1 g t 2 = g v 0 tan π / 6 v 0 cot π / 6 + 2 1 g g 2 v 0 2 cot 2 π / 6 = g v 0 2 ( 1 + 2 3 ) → v 0 2 2 g H = 5

Equation of trajectory is -
y = x tan θ − 2 V 0 2 c o s 2 θ g x 2
y = − 2 V 0 2 g x 2
d x d y = − V 0 2 g x
This is trajectory is perpendicular to planck when it hits it.
∴ m 1 m 2 = − 1
x = g 3 V 0 2
Also
x = V 0 t
∴ t = 3 g V 0
Now, tan ( 6 0 ) = ( 3 ) = H − 0 . 5 g t 2 V 0 t
Equating, we get-
2 3 g t 2 + V 0 t − 3 H = 0
Plugging in the value of t , we get-
V 0 2 2 g H = 5