Indestructible Lasagna Tower

Define length of lasagnas to be $L$ . Now, the center of mass is unaffected by any other dimension of the lasagna because the axis of rotation in consideration here is one into the page - thus any other dimension of the object does not contribute to the torque (and hence, center of mass) of the lasagna - only mass.

Let's say we make a stack. We want to find the number $N$ so that the total length of lasagnas that is overhang is $D$ . First, consider a specific case:

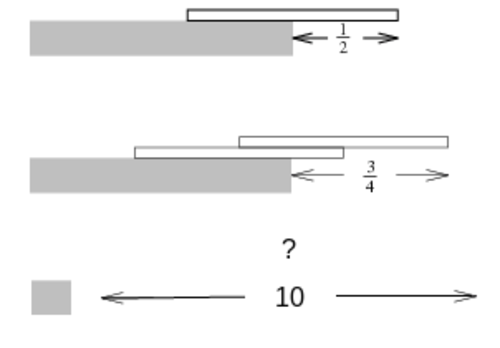
Say we want to find the number of lasagnas it takes before the top lasagna extends completely beyond the edge of the table. That is, $D>L$ . Let's say that we stack lasagnas in the following fashion: the top lasagna extends half its length beyond the second lasagna, the second lasagna extends a quarter of its length beyond the third, the third extends one sixth of its length beyond the fourth, and so on.

We want to show that the center of mass of the system of $N$ lasagnas lies above the table; that is, $\bar { x } <L$ . Draw an $xy$ plane, with origin at left the tip of the bottom book. Then, the $x-$ coordinates of the centers of mass of the lasagnas are

$x_1=\frac{L}{2}, x_2=\frac{L}{2(N-1)}+\frac{L}{2}, x_3=\frac{L}{2(N-1)}+\frac{L}{2(N-2)}+\frac{L}{2},$ and so on.

Each lasagna has the same mass $m,$ , so if there are $N$ lasagnas, then

$\bar{x}=\frac{mx_1+mx_2+...+mx_N}{mN}=\frac{x_1+x_2+...+x_N}{N}$

$=\frac { 1 }{ N } \left[ \frac { L }{ 2 } +\left( \frac { L }{ 2(N-1) } +\frac { L }{ 2 } \right) +\left( \frac { L }{ 2(N-1) } +\frac { L }{ 2(N-2) } +\frac { L }{ 2 } \right) +...+\left( \frac { L }{ 2(N-1) } +\frac { L }{ 2(N-2) } +...+\frac { L }{ 4 } +\frac { L }{ 2 } +\frac { L }{ 2 } \right) \right]$

$=\frac{L}{N}\left [ \frac{N-1}{2(N-1)}+\frac{N-2}{2(N-2)}+...+\frac{2}{4}+\frac{1}{2}+\frac{N}{2} \right ] = \frac{L}{N} \left [ (N-1)\frac{1}{2} + \frac{N}{2} \right ] = \frac{2N-1}{2N}L <L$

Thus, the center of mass lies above the table no matter how many lasagnas are added.

Also note that the series $\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+...=\frac{1}{2} \sum{\frac{1}{N}}$ is divergent (since it is a harmonic series). Hence, we can make the top lasagna extend any distance beyond the edge of the table if we add enough lasagnas.

Finally, observe that we do not have to follow the $\frac{1}{2N}$ scheme. In fact, any value of $a \ge 2$ will work for $\frac{1}{aN}$ . The series is still harmonic, and the center of mass $\frac{aN-1}{aN}L<L$ is still above the table.

I'm getting hungry. In fact, having a lasagna right now :)

For this one, use the approximate formula for the Harmonic function needed here

$\dfrac { 1 }{ 2 } \displaystyle\sum _{ n=1 }^{ x }{ \frac { 1 }{ n } } =\frac { 1 }{ 2 } \left( Log\left( x \right) +\gamma +\frac { 1 }{ 2x } -\frac { 1 }{ 12{ x }^{ 2 } } +... \right)$

otherwise, even computing time can get insane.

$\gamma = 0.5772156649...$ is the Euler-Mascheroni constant.

We also have to assume that the lasagna pieces are completely frozen solid and machined to perfectly identical blocks of aerospace quality.