2018 circles
The two rays in the diagram make an angle of 6 0 ∘ . The first circle is tangent to both rays and has radius 1. Each successive circle is tangent to the two rays and externally tangent to the previous circle.
The radius of the 2018th is a b , where a and b are positive integers with b maximized.
What is a + b ?
The answer is 2020.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
This intuitive visual way is beautiful. Thanks!
Why don't we use 2^2018 when we already knew that every single time the radius of the circle will double up over time?? That way we will get 2 as a and 2018 as b and we can sum them up into 2020. Are my theory wrong?? Can I use my solution?? Please confirm my theory, if you have time. XD
Log in to reply
it won't double, it will triple :)
Log in to reply
I don't understand at first but after I think of it, now I understand. Thanks for the reply XD
Unfortunately you've made a couple mistakes, even though you came to the same final number. The first is that the circle triples in size rather than doubles (you can see various proofs of this in the solutions below). The second mistake is that the power for the 2018th circle is 2017 rather than 2018, as the equation per circle is 3^(n-1). Consider circle 1, which has the radius 1. This can be expressed as 3^0, but not 3^1.
Log in to reply
Thanks for the correction!! Love seeing you replying and fixing the wrong one. This means you really understand the concept. Thanks again XD
Log in to reply
@Wise Akira – No problem! Glad I could help you understand the solution.
Great problem. Why is everyone assuming the first radius is 1? If it's 3 then a+b= 2021. Why must we assume that the expression 3^n must have n=0 for first circle? It's the first circle designated therefore n has to equal 1! I believe answer is 2021 unless problem specifies first radius equals 1. DE
Log in to reply
It says in the problem that the radius of the first circle is one.
Great similarity , but question was not clear I interpreted the numbers 1 2 3 4 as the radius of the circle But that was the number of circle
It looks intuitive but I don’t see any basis for smaller triangle to be one ninth of the larger.
As seen in the picture a right triangle can be constructed by connecting two centers of two circles. Let the center of the n'th circle be O n and the center of the n+1'th circle be O n + 1 . Let the radius of circle n be r n and the n+1'th circle r n + 1 . X n is the point where the triangle's right angle is.
The angle is
3
0
o
since it bisects the angle. Then we get that
s
i
n
(
3
0
o
)
=
2
1
. Since sin is opposite over hypotenuse
O
n
O
n
+
1
O
n
+
1
X
n
=
2
1
.
O
n
+
1
X
n
=
r
n
+
1
−
r
n
and
O
n
O
n
+
1
=
r
n
+
1
+
r
n
.
Then
r
n
+
1
+
r
n
r
n
+
1
−
r
n
=
2
1
2
∗
r
n
+
1
−
2
∗
r
n
=
r
n
+
1
+
r
n
r
n
+
1
=
3
∗
r
n
So the next radius is always three times as big as the previous. To get to the 2018'th circle there is 2017 steps. So we multiply the first radius of 1 by 3 2017 times which result in 3 2 0 1 7 .
a + b = 2 0 1 7 + 3 = 2 0 2 0
Same method :)
How do you prove the connecting line also bisects the angle
Log in to reply
The bisector of two tangents to the same circle always passes through its center.
Why On+1Xn is equal to the radius difference?
Distance from the center of the first circle to the vertex of the angle is 2. (Twice the radius of the circle.) So the distance from the vertex to the circle is 1, the same as the radius.
The same ratios apply to all the other circles. The distance from the vertex to circle number 2 is 3, so the radius of that circle is also 3.
Each circle has a radius 3 times that of the previous circle, so the last one has a radius equal to 3 2 0 1 7 , as there are 2 0 1 8 − 1 = 2 0 1 7 steps in the process.
The answer is 2 0 1 7 + 3 = 2 0 2 0 .
How did you figure out that the distance from the center of the first circle to the vertex is 2? Is there some theorem?
Log in to reply
From the value of a sine of 30 degrees.
In an equilateral triangle the incenter is the same as the centroid, and the centroid divides the median in ratio 1:2. (draw the common tangent line first, to see the triangle)
Let A be the centre PC and PB be the 2 tangents so ■BAC=180-60=120. So■PAC= 60 in right triangle PAC . Sin PAC = sin 60= 1/2=AC/PB. so PB=2. ■ means angle
hindsight is always 2020 :)
Why don't we use 2^2018 when we already knew that every single time the radius of the circle will double up over time?? That way we will get 2 as a and 2018 as b and we can sum them up into 2020.
"Why don't we...?" Because it doesn't. Also, the radius of the first circle is not 2^1 times itself, but 2 (or rather, 3)^0 times itself. Every time, the radius of the next circle triples the size of the last. The radius of the first circle is 3^0, or 1. The radius of the 2018th circle will thus be 3^2017.
Right answer, but from wrong assumptions.
Considering the first 3 cicrcles, You can find out that the distance from the vertex of the angle to the epcenter of the first circle is 2 (use metric relations in a semi equilateral triangle). Moving on the next circle, using the same method you can figure out that the radius of this circle is 3, and then the next one is 9. So, conjecture that the ith radius is 3^(i-1), and prove indcpucitively that the radius of the (i+1)th circle is 3^i. For i=2018, the radius is 3^2017, so 2017+3=2020.
O = Start point of the rays
M1, M2, ... = Center points of the circles
r1, r2, ... = Radii of the circles
T1, T2, ... = Tangent points at a ray
Triangle: O M1 T1; (M1 T1)=r1=1
1]: O M1 * sin 30° = r1 = 1
(O M1) = 1/ 0.5 = 2
(O M2) = 2 + 1 + r2 = 3 + r2
1]: (3 + r2) * 0.5 = r2
r_2 = 3^1 = 3
r_2018 = 3^2017
3+2017= 2020
i=1,2,3,...2018; r(i)=x(i)/2 ; r(i-1)=x(i-1)/2 ; x(i)=r(i)+r(i-1)+x(i-1) -> 2 r(i)=r(i)+r(i-1)+2 r(i-1) -> r(i)=3*r(i-1) -> r(i)=3^(i-1) -> r(2018)=3^2017 -> a+b=2020
Detailed Explanation:
Starting with the first circle, it can be broken up into 30-60-90 right triangles where the 30 degree angle is at the vertex of the angle, the right angle is where the circle is tangent to the angle, and the 60 degree angle is at the center. From there, it can be determined (using the rules of 30-60-90 triangles) that the gap between the first circle and the vertex has a length of 1 and it is known that the circle has a diameter of 2, making the distance to the second circle 3. This can also be split into a 30-60-90 triangle. Calling the radius of the second circle r 2 , we know the length of this triangle's smaller leg is r 2 and the hypotenuse is 3+ r 2 . Using the rules of 30-60-90 triangles, the radius of circle two is 3. This method can be continued and generalized into (using the fact of 30-60-90 triangles that the hypotenuse is twice the shorter leg)(where r n is the radius of the nth circle and d is the total distance of the hypotenuse tangent to that circle):
1 r n = 2 r n + d
2 r n = r n + d
r n = d
Which means the radius of some circle is the distance of the tangent hypotenuse to it. To get the tangent hypotenuse to the next triangle (which we now know is also that triangle's radius) we add together the diameter of the circle before it and all the distance before that, or:
r n = 2 r n − 1 + d
r n = 2 r n − 1 + r n − 1
r n = 3 r n − 1
So the radius of circle n is three times n − 1 . Using our knowledge that r 1 = 1 and r 2 = 3 , we can convert this into explicit form that
r n = 3 n − 1
Plugging in n = 2 0 1 8 gets 3 2 0 1 7 . The only way this could maximize b more in a b while keeping it an integer would be 2 s o m e t h i n g . Since 3 2 0 1 7 obviously only has factors of 3, this cannot be converted while keeping b an integer. Since the question is asking for a + b in a b , the answer is 3 + 2 0 1 7 = 2 0 2 0
Note: I am not very good at formatting things in this yet so if anybody knows how to put good pictures in and edit / highlight parts help would be very appreciated. Thank you.
Hmmm... Thats pretty neat!
It is forming an Geometric progresion whose first term (x) is 1 and common ratio (r) is 3 so that 2018th term is x*r^(n-1) Therfore on putting values we get a=3 and b= 2017
Let the radius of the first circle be a 1 and successive circles be a n where n is the number of the circle.
Now if we draw a line L which bisects the angle of the two rays, the line of the bisection will pass through the centres of the circles and make an angle of 6 π radians with the ray parallel to the x -axis.
Letting the distance of the between the intersection of L and the x -axis be denoted as l we find that l sin ( 6 π ) = a 1 → l = 2 .
Finally we can obtain this general formula for a n :
a n = 2 + r = 1 ∑ n − 1 a r where n ≥ 2
Evaluating the first few terms, we see that a 2 = 3 , a 3 = 9 , a 4 = 2 7 ⋯ a n = 3 n − 1 . As a result a 2 0 1 8 = 3 2 0 1 7 ∴ a = 3 , b = 2 0 1 7 and a + b = 2 0 2 0 .
I suggest that the (n + 1)th triangle is compared to the 'n'th triangle. And call the radius of the 'n'th triangle r and the radius of the (n + 1)th triangle R. The point that these triangles meet will be 30 degrees (I still do not have a character for degrees!?) since it will be half of the angle that the triangles are contained in. So looking from the 'horizontal' - [r + (r + R)xsin 30 degrees] = R. Hence [r + (r + R)/2] = R. Hence R = 3r. So the radius of each triangle is 3 times the radius of the previous one. As the first triangle has radius 1, the radius of the 2nd triangle is 3, the radius or the 3rd triangle is 3^2, and the radius of the 2,018 triangle is 3^2,017 And 3 + 2017 is equal to 2020!! Regards, David
For this problem I assumed that each circles were scaled by the same factor (X). I saw that the radius of Circle-x was Sin(30°)*Dx, where Dx is the distance between the center of Circle-x and the intersection of the 2 rays. As the radius of Circle-1 and Circle-2 are 1 and X, I can form these equations:
1 = S i n ( 3 0 ° ) ∗ D 1
D 2 = D 1 + 1 + X
X = S i n ( 3 0 ° ) ∗ D 2
I also added two more equation to verify my assumption that there is always the same factor X (just to be sure)
D 3 = D 2 + X + X 2
X 2 = S i n ( 3 0 ° ) ∗ D 3
Then I only needed to solve for X:
D 1 = 2 = > D 2 = 3 + X = > X = ( 3 = X ) / 2 < = > X = 3
And check with the two additional equations:
D 3 = 6 + 3 + 9 = 1 8 = > X 2 = D 3 / 2 is verified!
Thus, the 2018th circle as a radius of 3 ( 2 0 1 8 − 1 ) = 3 2 0 1 7
Therefore, the answer is 3 + 2 0 1 7 = 2 0 2 0 .
Simple. Using right triangle trig (30-60-90) the radii double after r=3. i.e. r=1,3,6,12,24, etc. This is 2^(n-2) * 3= 2^(n-2)*2^1.5) = 2^(n-0.5)=2^(n) (maximized) so a=2 and b=2018 so a+b = 2 + 2018 = 2020!
I solved this with the fact that the triangle formed when the (1) ray is bisected and the (2) tangent points and the corresponding centers of the circles are connected is a 3 0 - 6 0 - 9 0 Special Triangle . Because of this, the radius of the next triangle should be twice the hypotenuse of the previous triangle. Them. because a circle needs two radii to make a diameter, then when 2 r + 1 r (length of existing hypotenuse) = 3 r , repeat this and the general formula will be r n = 3 n − 1 . r 2 0 1 8 = 3 2 0 1 7 .
I solved this one in the same manner as Marta Reece, but I noticed a more visually intuitive solution:
As the angle is 6 0 ∘ , we can set each circle into an equilateral triangle by drawing a tangent line where each pair of circles meet. By splitting a larger triangle into 9 identical equilateral triangles like this: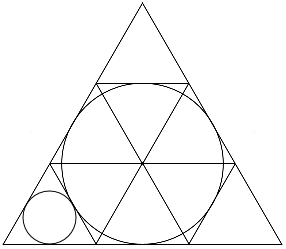
We can quickly see that each successive triangle is scaled up by three times the previous one, meaning the circle is also scaled up by three times. We can thus solve the problem using 3 2 0 1 7 (as the first circle has radius 3 0 ), which gives us 3+2017= 2 0 2 0 .