2016 Digital Root
For each number n , we define the Digital Root of n in the following manner: Take the sum of the digits to obtain a new number. Repeat this process until the result is a single digit.
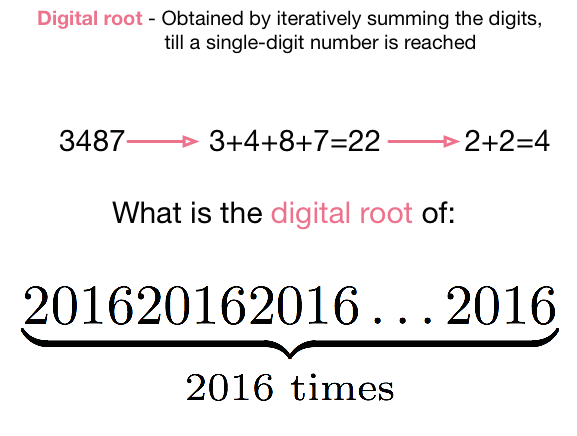
Find the digital root of 2 0 1 6 times 2 0 1 6 … 2 0 1 6 .
As an explicit example, for n = 3 4 8 7 , 3 4 8 7 → 3 + 4 + 8 + 7 = 2 2 → 2 + 2 = 4 . Therefore, the digital root of 3487 is 4.
Clarification : In the number above, 2016 appears 2016 times in its decimal representation.
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Firstly, note that the digital root of 2 0 1 6 is 2 + 0 + 1 + 6 = 9 . As 2 0 1 6 appears 2 0 1 6 times in the number we are asking for, then its digital root is equal to 2 0 1 6 ⋅ 9 = 1 8 1 4 4 → 1 + 8 + 1 + 4 + 4 = 1 8 → 1 + 8 = 9 .
Coincidentally, is the same digital root of 2 0 1 6 .
Note: The term in the question is actually digitial root . The digital sum is just the sum of the digits. I've edited the problem/solution accordingly.
It is not a co-incidence.
Check this out
inspired by your problem.
Log in to reply
Hi Vighnesh. Can you post the demonstration of why it is not a coincidence?
Log in to reply
Sum of digits is 9. If it occurs 'n' times then it is 9 n . For a number divisible by 9 , the sum of digits is also a multiple of 9. So , repeating this process till the end we get 9.
Log in to reply
@A Former Brilliant Member – Mmm clear. I thought that you had demonstrated when does the digital sum of n is equal to the digital sum of n t i m e s n . . . n . What should I check out?
Log in to reply
@Mateo Matijasevick – I guess that would be a more complicated problem.
2016=2+0+1+6=9 Number of occurance is 2016 which is independent to the answer
∴ answer is 9
y o u c a n a l s o c h e c k
2016*9=18144=1+8+1+4+4=18=1+8=9
Since the digital sum of 2016 = 9 So no matter how many time 2016 is there, the digital sum will always be 9.
Because every multiple of 9 has digital sum of 9...that's why that number is divisible by 9.