23/7 = 2 ?!?
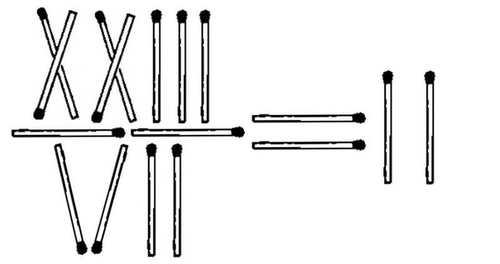This equation can be more or less corrected by moving only ONE matchstick. From where?
A. One of the X's.
B. One of the I's on the denominator
C. One of the I's on the numerator
D. The V.
E. One of the I's on the right hand side of the equation.
Clarifications and restrictions:
-
No tampering with the equals sign!
-
For a valid method, the matchstick that is moved has to be shifted to a different position altogether. For example, if you suggest A, the matchstick cannot remain in the numerator.
-
No Arabic numerals are allowed!
-
All Roman numerals formed must be conventionally accepted. For example, 4 should be represented as IV and not IIII.
That's about it, good luck solving folks!
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Discussions for this problem are now closed
7 2 2 = π
Yes! I know! That's why I said more or less you see!
Well I propose you put it on the = sign to make it = .
It perfectly satisfies the equation .
@Sualeh Asif – Ok taking what you said into account I will add a condition to the qn.
@Noel Lo – You also should add the condition that the = sign should not be changed or a number of solutions could occur.
@Sualeh Asif – the equation said no tampering with the equal sign.
@Daniela Florit – It was not there when i posted this.
P.s. I asked him to put that condition in! See below.
@Sualeh Asif – remove one match stick to one of the X so that XIIII = 14 and therefore, 14/7 = 2 :)
@Penn Paolo Necor – But 14 is written as XIV I guess
22/7=3.143 (not Pi, and 4.8% error). Turning the V into X (answer D) would yield 23/12=1.92 (4% error) - a much more accurate answer than the first attempt by almost 20% in accuracy improvement.
remove one match stick to one of the X so that XIIII = 14 and therefore, 14/7 = 2 :)
We have to move not remove the matchstick. ....it has to go smwhere after being taken out
XIIII its not a roman number, it written XIV
All Roman numerals formed must be conventionally accepted. For example, 4 should be represented as IV and not IIII.
read question properly
I have another solution. Since the question asked to move a matchstick to MORE OR LESS correct the equation, I assumed that both sides CAN be approximately equal too. So I chose 'D' i.e. to move a stick from the V in the denominator to make it X. The equation now reads 23/12 = 2 which is a very close approximation (23/12 is actually equal to 1.9).
Absolutely. I too discovered this solution and submitted according to this only. This question should have provision for both options.
Are you @Sagnik Ghosh reincarnated as @Sandeep Dhiman ? :P
There was a stipulation about the matchstick needing to be moved to an entirely different location (restriction #2). Kind of a dumb restriction though
Was my attempt too
I did that too following the 'more or less' hint. I also believe it should be a valid answer. C is not 'more correct' than D. Both are approximations, and without more information on border conditions (how approximate the answer needs to be) the choice is subjective. Huge thumb down for Birlliant on this one.
remove one match stick to one of the X so that XIIII = 14 and therefore, 14/7 = 2 :)
14 = XIV and not XIIII.
@Achyut Nair – Historically you can write XIIII. The render of 4 as IV was for saving space in some location. Please read http://en.wikipedia.org/wiki/Roman_numerals
hey Penn Paolo Necor we cannot write 14 as Xllll its wrong , it should be written as XlV
@Shivakumar Avadhani – Historically you can write XIIII. The render of 4 as IV was for saving space in some location.
@Alejandro Chavez – In that case I can read the right hand side of the equation which is 'II' as '11' instead too you know?
@Achyut Nair – Hi, I already added a note to say that no Arabic numerals are allowed.
@Noel Lo – Yeah but it also says ONLY Roman Numerals. π is not a Roman Numeral.
@Craig Lees – Hi Craig, sory for the misunderstanding. I will correct the problem!
This is perfect for the troll contest. xD
Hahaah thanks!!!!
@Satvik Golechha Can this be given as a troll contest entry?
Surely also you could move one of the sticks of the V to make the Denomiator XII, so 23/12 roughly equals 2?
for me i guess the best possible answer to this problem is to take a match stick away from one of the X, in that way, XIIII = 14. therefore, 14/7 = 2. right??/ ;)
Where does the other matchstick of the X go?
I found that changing the V to be X give you an more or less approximation 23/12 = 1.91 with a 2 in the other side. This is an error of 4.5%.
Pi factorial?
Remove on matchstick from the numerator and place it alongside ii to make it iii. It says approximately equal. So final equation is 22/7 = 3
pi would be an even closer approximation. :)
Technically a better solution is to remove a match stick from the second x, and placing it as the divider line for the fraction. This way, both sides are definitely equal, not just approximately.
Stupid, poorly-formed question! This is in NO WAY mathematics. 22/7=3.143 (not Pi, and 4.8% error). Turning the V into X (answer D) would yield 23/12=1.92 (4% error) - a much more accurate answer than the first attempt by almost 20% in accuracy improvement.
Hi Gregory, I see what you mean so I think what I can do is to add that the matchstick moved has to be shifted to a different position altogether.
this is just not a math problem. It's not broken and doesn't need to be fixed, it's from a completely different field. Also, if you would have started with 22/7=2, there would have been a precise answer: 21/7=3. Why start with 23?!
just to clarify: you can solve a math problem any number of ways and arrive to the same answer. Getting the best answer and then being judged on the correctness of your way isn't what the field of mathematics is about.
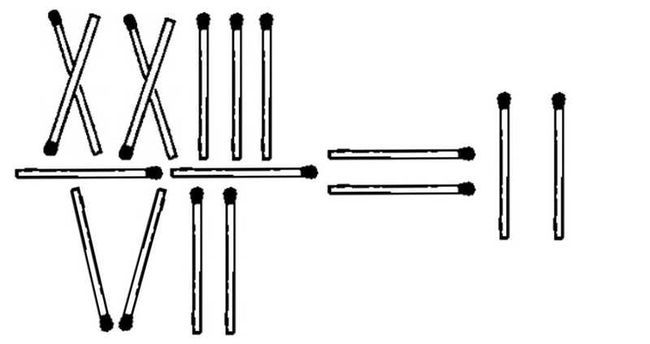Means
23/7 = 2. We can make it.........
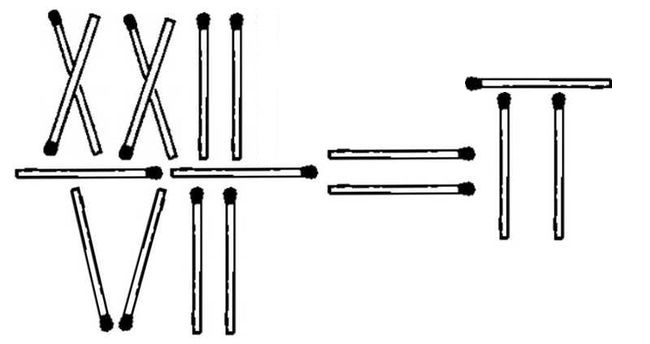
that is 22/7 = π
Take 1 stick from the numerator to make it 22 then put it on the RHS of the equation to make it 3 ........SO, 22/7 = approximately 3
Yeah that too is right but its not going to change the answer of the question in any way. :P
Sir! This is also approximate what if 23/12 = 1.9
Move one of the I's from the top to create a V with the second I from the bottom. Now we have 22/11=2
You mean VVI to represent 11? No 11 is represented by XI.
If you remove 1 from the denominator and move it to the solution to make a "V" then you have XXIII (23)/VI(6) which is approximately equal to IV (4).
try to adjust one stick of V going left to make it X . Then cancell XII . what left is X1 = 11 HAHHAHA
Just remove one stick and put it on top of the others two sticks and that forms pi, that equation is close to that number
This is NOT strict enough. First you say "moving matchstick", not "remove matchstick". Second "VIIII" is on the wrong order of Roman number so that the main problem of this is "logic problem"
from the numerator we just remove one matchstick from the second x and after removing it I just stand straight that remaining stick .
XX|||/\/||| ->X||||/\/|| = ||. that's all.
Move from one of the I's on the numerator such that the numerator reads 22. Place the matchstick on top of the II to make it π so that we now have 7 2 2 = π !