3 Cheers for Geometry !!
The sides a,b,c of a Δ ABC are in Geometric Progression whose common ratio is 3 2 and the circumradius of the triangle is 6 × 2 0 9 7 .
Find the longest side of the triangle .
The answer is of the form n m where m and n are co-prime numbers ;
Find m n .
You can try more of my Questions here .
The answer is 2401.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Actually this the way I did it .
Happy to see that there is someone who thinks like me !!!!
Hi, its been a long time since I solved a question of yours what happened , can you post one sooner?
I'll be waiting !!!
Let the longest side length be a , b = 3 2 a , c = 9 4 a , the center of the circumcircle be O , its radius r = 6 × 2 0 9 7 , ∠ A B O = α and ∠ O B C = β .
Using Cosine Rule, we have:
⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ b 2 = a 2 + c 2 − 2 a c cos ( α + β ) r 2 = c 2 + r 2 − 2 c r cos α r 2 = a 2 + r 2 − 2 a r cos β ⇒ cos ( α + β ) = 7 2 6 1 ⇒ cos α = 9 r 2 a ⇒ cos β = 2 r a . . . ( 1 ) . . . ( 2 ) . . . ( 3 )
We know that:
cos ( α + β ) = cos α cos β − sin α sin β
⇒ 7 2 6 1 = 9 r 2 a × 2 r a − ( 1 − 8 1 r 2 4 a 2 ) ( 1 − 4 r 2 a 2 )
⇒ 7 2 6 1 − 9 r 2 a 2 = − ( 1 − 8 1 r 2 4 a 2 ) ( 1 − 4 r 2 a 2 )
⇒ 5 1 8 4 3 7 2 1 − 3 2 4 r 2 6 1 a 2 + 8 1 r 4 a 4 = 1 − 3 2 4 r 2 9 7 a 2 + 8 1 r 4 a 4
⇒ 9 r 2 a 2 = 5 1 8 4 1 4 6 3 ⇒ a 2 = 5 1 8 4 ˙ 2 0 9 1 4 6 3 ˙ 9 ˙ 3 6 ˙ 7 = 1 6 4 9
⇒ a = 4 7 ⇒ m n = 7 4 = 2 4 0 1
Nice solution but there was an easy way R=(abc)/(4*Area),where you apply Heron's formula for the area of the triangle
Nice solution Sir
Log in to reply
Nice question, actually.
Log in to reply
Thanks sir.
Sir, from where did you practice Geometry since it's almost as if it's your strong point ,right ?
Log in to reply
@A Former Brilliant Member – I am a retired person and I have a lot of time practicing math on Brilliant.org. Just digging through what I have learned 30 years ago and start practicing. Geometry hasn't changed much over the years. In fact, I didn't learn about incircle, circumcircle, centroid back then. I just picked up through the internet. Work hard and you will be as good if not better.
We know in usual notations
R
=
4
∗
A
r
e
a
p
r
o
d
u
c
t
o
f
s
i
d
e
s
.
L
e
t
t
h
e
s
i
d
e
s
b
e
1
8
x
,
1
2
x
,
a
n
d
8
x
.
∴
s
=
1
9
x
,
A
r
e
a
=
1
9
∗
1
∗
7
∗
1
1
∗
x
2
.
⟹
4
∗
1
9
∗
1
∗
7
∗
1
1
∗
x
2
1
8
∗
1
2
∗
8
∗
x
3
=
4
∗
7
∗
2
0
9
1
2
3
x
=
R
=
6
∗
2
0
9
7
.
S
o
x
=
7
2
7
.
∴
B
i
g
g
e
s
t
s
i
d
e
=
1
8
x
=
4
7
=
n
m
.
S
o
m
n
=
7
4
=
2
4
0
1
.
We have a triangle of sides a , 3 2 a and 9 4 a , inscribed within a circle of radius 2 0 9 2 5 2 .
By the Cosine Rule, a 2 = ( 3 2 a ) 2 + ( 9 4 a ) 2 − 2 × 3 2 a × 9 4 a × cos θ , where θ is the angle opposite a ,
⟹ 8 1 2 9 a 2 = − 2 7 1 6 a 2 cos θ ,
⟹ c o s θ = − 4 8 2 9 .
Using the identity cos 2 θ = 2 cos 2 θ − 1 , we have that cos 2 θ = − 1 1 5 2 3 1 1 (a calculator could have been used here instead).
Knowing that the angle at the centre is twice the angle at the circumference, we can form a triangle of lengths a , 2 0 9 2 5 2 and 2 0 9 2 5 2 , where the angle opposite to a is 2 θ .
By using the Cosine Rule a second time, we have that a 2 = 2 0 9 5 0 4 − 2 0 9 5 0 4 cos 2 θ ,
⟹ a 2 = 1 6 4 9 (by substituting cos 2 θ = − 1 1 5 2 3 1 1 ),
⟹ a = 4 7
The longest side of the triangle is a , which implies that m = 7 and n = 4 ,
∴ m n = 7 4 = 2 4 0 1
The diagram below, in which x = θ , r = 2 0 9 2 5 2 , and C is the center of the circumcircle may also aid my explanation (or not!)
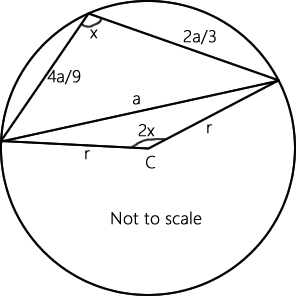

Let the sides be a = 2 3 x , b = x and c = 3 2 x . Now use the formula for the circumradius:
R = ( a + b + c ) ( a + b − c ) ( a − b + c ) ( − a + b + c ) a b c
6 2 0 9 7 = 3 6 1 4 6 3 x 2 x 3
2 0 9 7 = 7 2 0 9 6 x
x = 6 7
Finally, the longest side is a :
a = 2 3 ⋅ 6 7 = 4 7 ⟹ m = 7 ⟹ n = 4
So, the final answer is 7 4 = 2 4 0 1 .