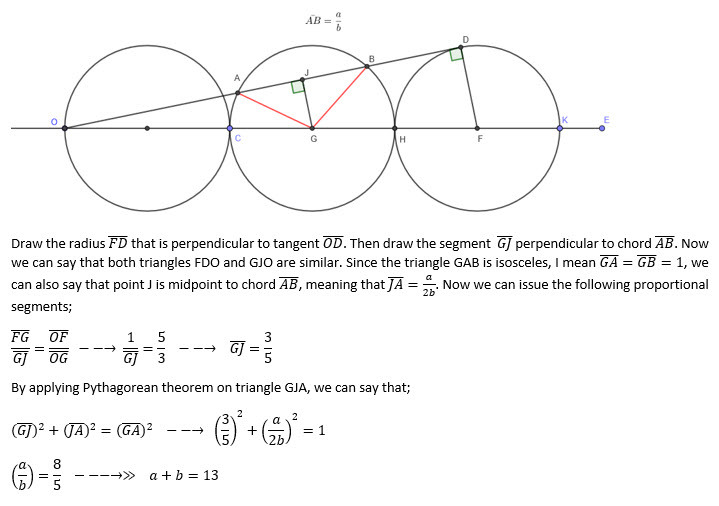
3 Circles and a Line
Three unit circles are drawn tangent to each other with all their centers lying on line segment O E .
From O , line segment O D is drawn such that it's tangent to the rightmost circle.
If the length of the chord A B is b a , where a and b are coprime positive integers, then what is a + b ?
Note: I did not create this problem; I simply solved it and decided to post it on here. Credit goes to my math teacher.
The answer is 13.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
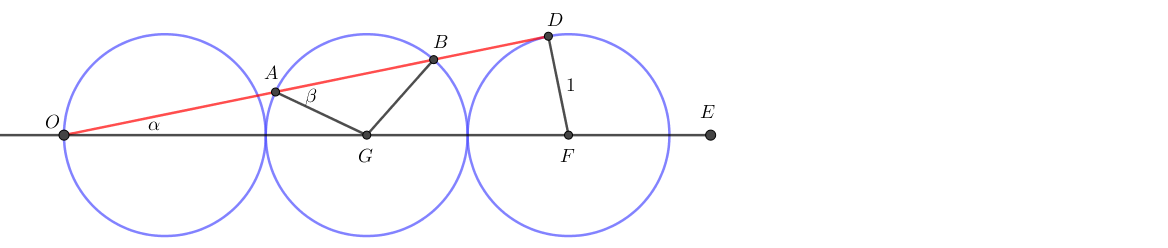 sin
(
α
)
sin
(
β
)
O
G
sin
(
β
)
G
B
2
A
B
=
O
F
D
F
=
5
1
=
sin
(
α
)
A
G
=
5
3
=
A
B
2
+
A
G
2
−
2
A
B
×
A
G
cos
(
β
)
=
5
8
sin
(
α
)
sin
(
β
)
O
G
sin
(
β
)
G
B
2
A
B
=
O
F
D
F
=
5
1
=
sin
(
α
)
A
G
=
5
3
=
A
B
2
+
A
G
2
−
2
A
B
×
A
G
cos
(
β
)
=
5
8
Why does sin of alpha equal DF over OF?
Log in to reply
In a right angle triangle, sine = hypotenuse opposite .
Tangents are perpendicular to the radius sharing the common point
How do I get the value of cos beta? Or is it always 4/5 when sin is 3/5?
Log in to reply
If sin ( β ) = 5 3 , then cos ( β ) = 5 4 when β is in the first quadrant.
You can get the value of cos(b) if you draw a right triangle with ratio from sin(b), and use the Pythagorean theorem to calculate the length of the leftover side. Also, you can calculate the value from the formula sin^2(a)+cos^2(a)=1. This formula allows you to calculate the value of sin or cosine when you have the value of the other one(with the same angle).
Can someone explain the second line (OG/sin(beta)=AG/sin(alpha))?
Log in to reply
sin(pi-beta)=sin(beta)
It is the sine rule.
This is awesome ❤️ I did it in tedious manner with Cartesian geometry
Log in to reply
I think coordinate geometry way is way cooler. Far more maths involved and more learning for my students than the trig way. Many of my students could do the trig way but they all learned something the coordinate geometry way. Give yourself some credit! :-)
Why OG/sin(β) = AG/sin(α) ?? Someone said it's the law of sines, but these segments aren't opposite to the referenced angles; and someone else talked about right triangles, and these aren't right triangles. I'm still confused by that line.
Log in to reply
The angle opposite to O G is equal to π − β . In my use of the sine rule, the sin ( β ) = sin ( π − β ) .
Angle D is a right angle since O D is tangent to the circle that passes through D .
This has a nice solution by applying inversion with respect to central circle. No trigonometry needed in that case.
Abraham really should have mentioned 2 points: Angle ODF is 90 degrees so sin(ODF) = 1 Triangle ABG is isosceles, and he really should have placed beta at angle ABG to use the sine rule. These points are rather obvious though.
GB^2 = AB^2 + AG^2-2 AB AG cos(β) ?
Let l=AB. Draw a perpendicular GH from G to AB. Note that H is the midpoint of AB since GH is drawn perpendicular to AB. Moreover, triangles OGH & OFD are similar hence: F D G H = 5 3 ; hence GH = 5 3 since FD =1. Now,from right tr. AGH, 4 l 2 =1 - 5 2 3 2 or l = AB= 5 8 .
Yes! This is the solution I used! You might need to include a few details, though.
Log in to reply
It's great for the 3rd grade trigonometry lesson, so I'll include it in my notebook (if you don't mind). I like Zhang's solution because he used both sine and cosine rules and a useful property sin x = sin (180 - x) (and, of course, the right triangle definition of the sine). Thank you very much for sharing this problem.
This is by far the simplest method to solve this problem. You might need to add a few details so other people can follow your logic. The similar triangles are OHG and ODF. The last line refers to another right angled triangle AHG. Since AH is half of AB, the answer is AH x2.
"Note that H is the midpoint of AB since" AG and BG are equal, (so AGB is an isosceles triangle) and "GH is drawn perpendicular to AB"
It's how I did it, but I made a mistake in the very last step, I forgot to take the square root basically. I calculated AH (but ACTUALLY calculated AH², which is 16/25), then took twice that to get a length AB of 32/25. oops
Lets plot this figure on Cartesian Plane. O will be Origin.
We get G = ( 3 , 0 ) and F = ( 5 , 0 )
Equation of circle with center G will be ( x − 3 ) 2 + y 2 = 1
Equation of Circle with center F will be ( x − 5 ) 2 + y 2 = 1
Let the tangent line meet the Circle ( F centered) at D ( p , q )
In traingle O D F , using Phythagoras Theorem, we get O D = 5 2 − 1 2 = 2 6
To calculate p and q , we have folllowing equations,
p 2 + q 2 = 2 4 and ( p − 5 ) 2 + q 2 = 1
We get q = 5 2 4 and p = 5 2 4
We get the equation of the tangent line as x = 2 4 y
We now find the points of intersections of this line with ( x − 3 ) 2 + y 2 = 1
We get two points as B = ( 2 4 ( 2 5 3 2 4 + 4 ) , 2 5 3 2 4 + 4 ) and A = ( 2 4 ( 2 5 3 2 4 − 4 ) , 2 5 3 2 4 − 4 )
We get A B = 2 5 8 ( 2 4 ) 2 + 1 2 = 2 5 8 × 5 = 5 8 = 5 8 = b a
Therefore, a + b = 8 + 5 = 1 3
Interesting take with the Cartesian plane! Never would've thought of that approach!
Log in to reply
You can even solve 3-D objects having symmetry using this. Now, you can even calculate AF, BF ,etc if you want!
Where did you get any numbers from in the first place? I'm sure its logical it's just not clicking for me
Log in to reply
Sorry, I didn't get which numbers you are talking about. Can you be more precise please?
Log in to reply
The description doesn't give any number for me to work with however denis says the radius is 1. Where did the 1 come from?
Log in to reply
@Wes Mok – Pick any other number and you'll end up simplifying a the and and get an answer equal to the answer you would've gotten if you picked radius = 1 from the beginning.
@Wes Mok – The question states three "unit" circles. Here, "unit " implied that they have radius equals unity which is definitely equals 1.
Radius = 1.
I did everything same except the OD part. I misinterpreted as hypotenuse and ended up with some radicals😁
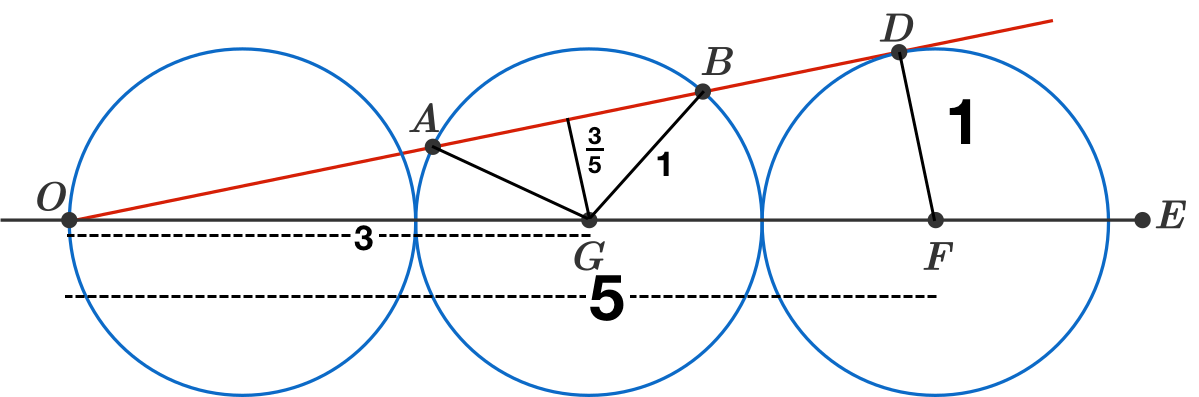 By comparing to similar triangle
△
O
D
F
, we can see that the line from
G
which bisects the chord
A
B
has a length of
5
3
. Using Pythag, we can work out the length of
2
A
B
:
By comparing to similar triangle
△
O
D
F
, we can see that the line from
G
which bisects the chord
A
B
has a length of
5
3
. Using Pythag, we can work out the length of
2
A
B
:
( 2 A B ) 2 ( 2 A B ) 2 ( 2 A B ) 2 2 A B A B = 8 + 5 = 1 2 − 0 . 6 2 = 1 − 0 . 3 6 = 0 . 6 4 = 0 . 8 1 . 6 = 5 8 = 1 3
This is exactly how I solved it!
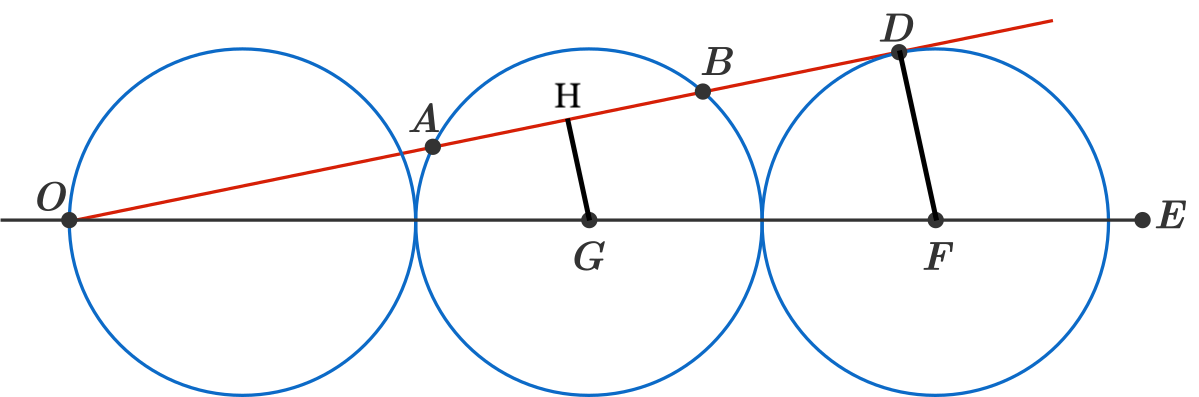
∆ OHG ~ ∆ ODF (AA similarity)
=> O F O G = F D G H
We know OG = 3 units, OF = 5 units and FD = 1 unit => HG = 5 3 units
If the perpendicular distance of a chord from the centre is given then length of the chord can be calculated easily using Pythagoras theorem.
=> AB= 2*sqrt(1- 2 5 9 ) = 5 8 .
nice answers!
From trigonometry on △ D E F we have O D = 2 6 and cos O = 5 2 6 .
From the power of a point theorem , the two secants to circle G have the relation O A ⋅ O B = 2 ⋅ 4 , or O B = O A 8 .
From the law of cosines on △ O B G , B G 2 = O B 2 + O G 2 − 2 ⋅ O G ⋅ O B ⋅ cos O , or 1 2 = ( O A 8 ) 2 + 3 2 − 2 ⋅ 3 ⋅ O A 8 ⋅ 5 2 6 , which solves to O A = 5 6 6 ± 4 .
This makes O B = O A 8 = 5 6 6 ∓ 4 , which means A B = O B − O A = 5 8 . Therefore, a = 8 and b = 5 , and a + b = 1 3 .
Draw a perpendicular GH from G to AB and let l=AB. Now by similar triangles: GH/FD =3/5; hence GH =3/5 since FD =1. Now, l²/4 =1 - (3/5)² or l = AB= 8/5.
Log in to reply
Great solution! You should post it in the solutions section so people can upvote it.
Log in to reply
Seconded - much neater than my solution! (As I mention in another comment, it's really interesting to see so many different approaches)
Okay thanks, guys. I've posted it as advised.
If you were told, "find a point P on the line O D satisfying P G = 1 ," you would spot that there are two such points: A and B . This ambiguity is an example of the solution of a triangle Δ P O G , knowing only two sides and a non-included angle (see here , for example). We have the following information about Δ P O G :
-
O G = 3 (since the circles have unit radius)
-
P G = 1
-
sin ∠ P O G = 5 1 (since ∠ P O G = ∠ D O F , O F = 5 , D F = 1 and ∠ O D F = 9 0 ∘ )
We're interested in the side length O P ; let's call this x . By the cosine rule, P G 2 = O P 2 + O G 2 − 2 O P ⋅ O G cos ∠ P O G .
Substituting, this is 1 2 = x 2 + 3 2 − 6 x cos ∠ P O G . Note that this is a quadratic in x , with - as we'd expect - two solutions.
Rearranging and completing the square, this becomes x 2 − 6 x cos ∠ P O G + 9 cos 2 ∠ P O G = − 8 + 9 cos 2 ∠ P O G
Plugging in sin ∠ P O G = 5 1 this becomes ( x − 3 cos ∠ P O G ) 2 = − 8 + 9 ( 1 − 2 5 1 ) = 2 5 1 6
Taking square roots, x = 3 cos ∠ P O G ± 5 4
The two solutions correspond to the lengths O A and O B ; we want A B , the difference of these, which is just
( 3 cos ∠ P O G + 5 4 ) − ( 3 cos ∠ P O G − 5 4 ) = 5 8 , so the required answer is 8 + 5 = 1 3
Nice solution! It was very similar to mine, but the only trigonometry I used was the Pythagorean Theorem.
Log in to reply
Thanks - you should post your solution! I find it really interesting to see different approaches. I originally used coordinate geometry, as per Niraj Sawant's solution - after all, you called one of the points O , so how could I resist? - but then started trying to angle hunt ∠ A G B in order to find the chord length; that led to my posted solution. Fun fact: the length of the chord in the leftmost circle is irrational. I wonder what makes the middle circle special. If we had different numbers of circles, would we still find rational chords?
The solution lies on our perspective as O is 1 and A is 2 B is 3 but actually I just a pythagorean theorem thingy 2^2 + 3^2 = 13 or c^2
I think you missed a few steps. Also, that is just incorrect.
Let X be the midpoint of AB. GX is perpendicular to AB.
GOX is similar to FOD, so GX=FD*GO/FO=3/5.
AX²=AG²-GX²=1²-(3/5)²=(4/5)².
AB=2AB=8/5.
Drop a perpendicular from G on chord AB, which can be easily proved=(3/5). Use Pythagoras to show
AB=2(√1-(9/25))=(8/5)
Answer=13
Let t be the mid-point of AB. Tan(<DOF) = 1/2.5 = .4. TG/OG = .4 = TG/1.5, TG = .6, TB = .8, AB = 1.6 = 8/5, 8 + 5 = 13. Ed Gray