3 coins
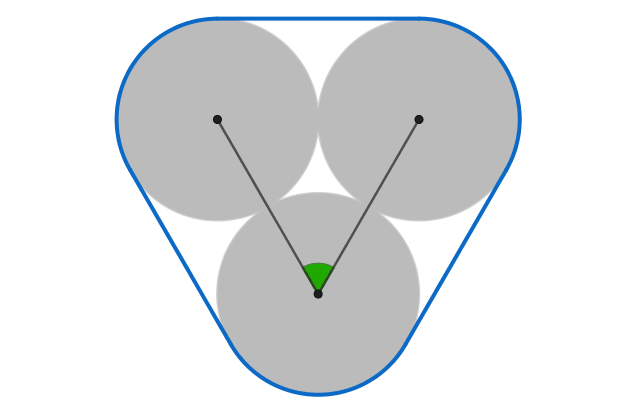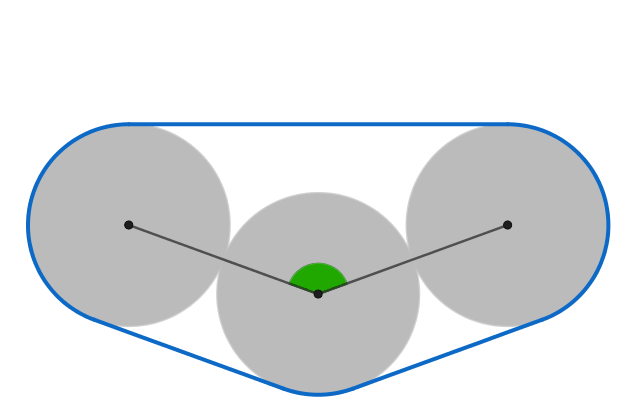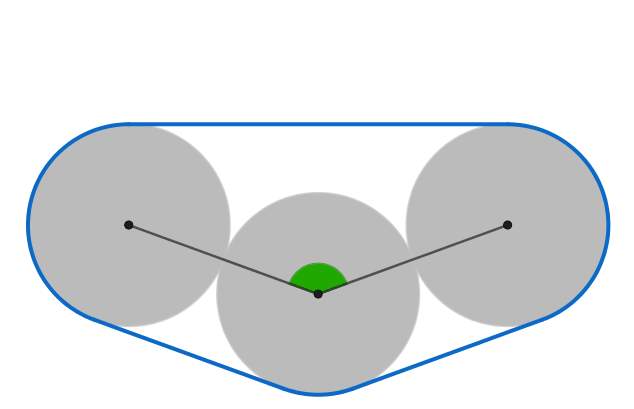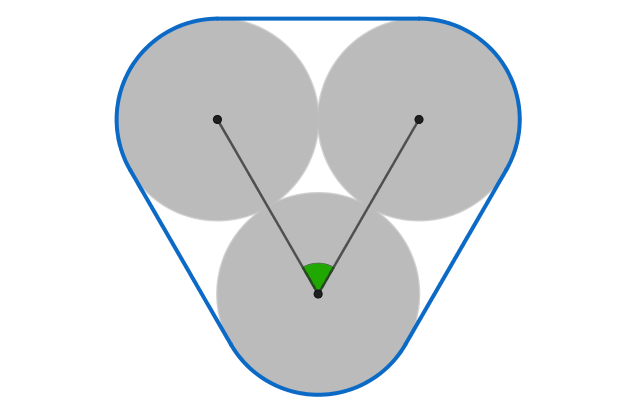
The centers of three identical coins form the angle that's colored green above.
What angle maximizes the area of the blue convex hull?
Note: You can imagine the perimeter of the convex hull as a rubber band stretched around the three coins.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
You need to address that the solution to A ′ ( θ ) = 0 is the global maximum and not just an extrema.
Log in to reply
Just make a quick graph, then. I don't mean to sound rude but this isn't a calculus exam.
Log in to reply
Jeremy, I also found a simple formula that can directly calculate the changing area would be assuming the radius of all the circles are 1. Here it is:
Area = 4cos(x)(sin(x)+1)-pi The way I approached it was a bit different than yours but your answer almost looks like mine so I decided I could share this one with you and see what you thought about it. If you want me to explain how I got this answer I am more than glad to share that as well.
Also, if you don't know what I mean by the changing area I mean the section where the area changes depending on the angles given. Look for John McLaughlin's post below to see what I mean (it's the blue area).
Log in to reply
@Xxtheuniversexx . – Oh yeah and the angle you plug in would be the CAB angle or the ACB angle (doesn't matter since both angles will always be the same).
The way to remedy this would be to show that A ( 6 0 ) is greater than A ( 3 0 ) and A ( 9 0 ) , correct?
Log in to reply
Or the second derivative test: for θ between 0 and π / 2 , the second derivative − 8 sin 2 θ − 4 sin θ is always negative, so the local maximum must be a global maximum.
Right. And you find the minimum which is at $\theta = 90$.
So the answer is 120 degrees?
Used the same rules. I made a geogebra figures that helped me solve it. If you want to have a look : geogebra You can move the blue dot for various angles
Log in to reply
This is how I checked my solution was correct.
I used the same approach, based on the insight that that only the rectangle-triangle region ever changed in area and that the three set of circle regions defined by the various lines each preserved a full circle's area regardless of angle, but used the algebraic expressions from the Pythagorean theorem, area as a function of the altitude of the triangle (ranging from 0 at 180 to √3 at 60) instead of the trig functions. Evaluating the derivative of that function (using unit circles) produced a maximum at h = 1 (and minimum at h = 0) corresponding to an angle of 120 degrees.
Does anyone know how to create this gif animation in geometers sketchpad. I can animate the circles but I am unsure how to wrap the "elastic band" around them.
Log in to reply
Construct the relevant radii as perpendicular to the segments joining the centers of the circles to get the points. Then construct the three segments and three arcs and make them the same color and thick.
Can you make animated gifs in gsp?
Log in to reply
Thanks for the tips. I managed to get it right. I haven't been able to get the gif part just yet but this link from the GSP website is my starting point.
http://www.dynamicgeometry.com/Technical Support/FAQ/Sketchpad and the Internet/Web_Options.html
The maximum and minimum angle measure of this are 180 and 60 respectively. So for the optimum area, it will be the median of these measures. Thus, (180+60)/2 = 120.
Excellent! I too solve such problems dealing with geometry through this very intuitive method........
I solved it by eyeballing the animation... can you justify why the mean is the solution?
That intuition worked in this instance, but it assumes that the graph of area for angle is symmetric. In other problems, that assumption will be wrong.
in order to use the mean angle value, you need to show that the function linking the angle to the area is linear (which is not obvious)
I love simple answers :)
Hand waving.
I did no math for this, but I already knew from rock climbing that a 120-degree angle in your anchor creates maximum tension (that's very bad). So 120 degrees was likely to be the most 'stretched' angle for the blue band.
Very nice!
I think it’s brilliant that 2 seemingly unrelated activities could link together like this
I don't know whether or not this is valid, in this case, tension is proportional to the length of the band, which is 2 π r + 4 r + 4 r sin ( 2 θ ) , where θ is the vertex angle of the isosceles triangle formed by the centers of the circles, and that maximizes at θ = π .
Also, If I'm imagining this correctly, the tension in an anchor angle θ would be proportional to sec ( 2 θ ) , which sure is big at θ = 3 2 π , but it goes to infinity as θ aproaches π . But I know nothing about rock climbing, you might me talking about something else.
street smarts :)
Relevant wiki: Optimization
 The light and dark gray areas are constant, so we must maximize the blue area.
The light and dark gray areas are constant, so we must maximize the blue area.
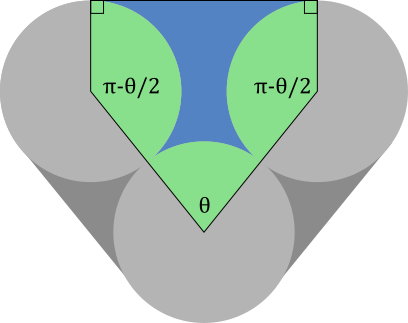 The blue area is the area of this pentagon minus the three green sectors. If we set the circle radii to be 1, the area of a sector is half the angle, so we have:
The blue area is the area of this pentagon minus the three green sectors. If we set the circle radii to be 1, the area of a sector is half the angle, so we have:
A g r e e n = 2 θ + 2 ( π − 2 θ ) = π
Therefore the problem reduces to maximizing the pentagon area, which is equivalent to maximizing one half as follows:
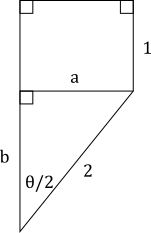
By basic trigonometry:
b a 2 + b 2 b d a d b = 2 cos 2 θ = 4 = 4 − a 2 = 2 1 4 − a 2 1 ( − 2 a ) = − b a
Now the area to maximize is the area of the rectangle plus the area of the triangle and the solution is where the gradient with respect to a is zero:
A d a d A = 0 = a + 2 a b = a ( 1 + 2 b ) = 1 + 2 b + a ( 2 1 d a d b ) = 1 + 2 b − 2 b a 2 = 1 + 2 b − 2 b 4 − b 2 = b + 2 b 2 − 2 + 2 b 2 = b 2 + b − 2 = ( b − 1 ) ( b + 2 )
and since 0 ≤ b ≤ 2 we have b = 1 . To confirm this is a maximum, we can easily show that the second derivative at b = 1 is − 3 3 .
We could now calculate θ using an arccos , however it's clear that the triangle above is the 1 , 2 , 3 triangle making 2 θ = 6 0 ∘ and θ = 1 2 0 ∘ .
Instead of using geometry like Jeremy Galvagni , I used processing and plotted all the points for the three circles, then ran a convex hull calculator to calculate the convex hull around all three circles, filled in that shape with red, and then counted up all the red pixels. I did this for every angle, and then found the angle that gave the greatest number of red pixels.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 |
|
My congratulations to the developer of the convex hull calculator. "instead of using" might better read ":Instead of solving the problem."
Even allowing that pixel counting (probably) gives the correct answer, and that checking only the given answers in a multiple choice quiz is sometimes a good practical test-taking tactic, but it gives little insight into this problem. For example, you get no assurance that any of the given answers is the true maximum. (Nor do you need that if the only objective is to get past the question.)
This approach is appropriate for a problem for which approximation methods are the only alternative. But even then there must be some solid theory behind the approximation method that insures that the computation is sound. (I wonder if those stories about the rocket going the wrong way because someone assumed a divergent series converged are true or merely urban legend?)
I prefer infinitesimals to pixels.
Intuitively, I guessed that the area would be max when all the three sides are the same which would be when angle between the known vectors is 1 2 0 0 .
Huh. I just figured that if the lowest areas correspond to 60 degrees and 180 degrees, then the largest area would be halfway between the two at 120.
Not even hand waving.
Observe when more than 120 degree, area is decreasing.
Relevant wiki: Extrema - Problem Solving - Medium
The orange rectangles also do not depend on the angle we can ignore them too.
Let the coins have radius 1 and the angle be 2 θ then the triangle has area 2 sin 2 θ and the blue rectangle has area 4 sin θ so the area as a function of θ is
A ( θ ) = 2 sin 2 θ + 4 sin θ
A ′ ( θ ) = 4 cos 2 θ + 4 cos θ
Solving A ′ ( θ ) = 0
4 cos 2 θ + 4 cos θ = 0
2 cos 2 θ + cos θ − 1 = 0
cos θ = 2 1 o r cos θ = − 1
θ = 6 0 o r 1 8 0
2 θ = 1 2 0 o r 3 6 0
The solution that makes sense is 2 θ = 1 2 0 d e g r e e s
Note this picture is not the exact solution but it is close. The middle circle would have to be tangent to the line joining the other circles' centers.