3-D Tiling
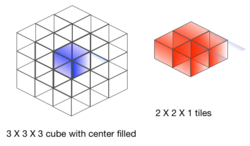 Consider a
3
×
3
×
3
grid with the center cube filled. There are 26 cubes remaining. How many
2
×
2
×
1
tiles could we place without overlapping?
Consider a
3
×
3
×
3
grid with the center cube filled. There are 26 cubes remaining. How many
2
×
2
×
1
tiles could we place without overlapping?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
3d model of the solution: https://skfb.ly/ES6B
Every 2 × 2 × 1 tile will occupy one side of the center cube. Since the center cube has 6 sides, exactly 6 tiles will fit. If each of these tiles keeps the tile in the same corner, then we know that these tiles will not overlap.
The volume of the 3 x 3 x 3 cube, as stated, is 26 cube units since the center cube is occupied. The volume of the 2 x 2 x 1 cube would be 4 cube units. So, if you divide 26 by 4, the quotient would be equal to 6, with a remainder of 2 units. So, six 2 x 2 x 1 cubes would fit in the region without overlapping.
This is just an idea. I think this is the solution because this is the first of infinitely many configurations of 2 × 2 × 1 tiles that would give us a cube with odd dimensions (not necesarilly filled, but what is important here is that it gives the dimmensions). The key is parity. When we try to construct a cube (different from the easy 2 × 2 cube), we first Take two tiles and connect them forming an "L". Then notice that the dimensions of this figure are 2 × 2 × 3 . Then connect another "L" but in opposite direction and you form a 3 × 3 × 3 , figure. However, another "L" can be incorpored to the figure keeping the same dimmensions, leaving three spaces that form a diagonal through the cube. I know this maybe isn't that clear, but at least I tried... Maybe someone can state what I'm traying to say more clearer. Sorry for my bad english :)
[This was a wrong solution.]
Okay, maybe I'm just not reading this question correctly. If we eliminate 2 opposite corner cubes from the remaining 26 cubes, we can array three 2x2x1 tiles around one missing cube, and three more 2x2x1 tiles around the other.
What is the one-line solution, because maybe it'll help me find the solution to that other problem.
Log in to reply
Yea, you're right, we can put 6. Darn it. i miscounted in my argument, and this is now less interesting with the answer of 6.
But that's exciting! In relation to the inspiration problem:
If we can fit 4 cubes on a face with 2 (adjacent) edges restricted off, then we can fit 6*4 of them! Of course, we can't do 4 on a complete restriction, but it seems likely that we could do a "loose" restriction where we allow slight overlap that is accounted for in the packing.
We also have the opposite corner cubes to play with!
Log in to reply
Okay, you can always delete this post, but I'd still like to hear that one-line solution. I like leaving no stone unturned. Even mistakes can be valuable.
Log in to reply
@Michael Mendrin – My faulty solution was:
Each 2 ∗ 2 ∗ 1 square must cover 2 "edge" cubes (IE not corner, not middle). However, i miscounted and thought that there were only 8 edge cubes, but there are actually 12.
Log in to reply
@Calvin Lin – Unfortunately, I've got to go now, gone for a couple of days. As I said in my reply to you in that other problem, I do think it's possible for 8 red cubes to touch one of the faces of the blue cube, but the solution is a mess and will take some time to forward an accurate graphic of how it's done. Unfortunately, even that will not get us any closer to a 24 solution.
Let A, B, C, D, E and F be the tiles and x be the filled center cube. Here we go: