3 dots in a triangle
You and a friend decide to play the following game:
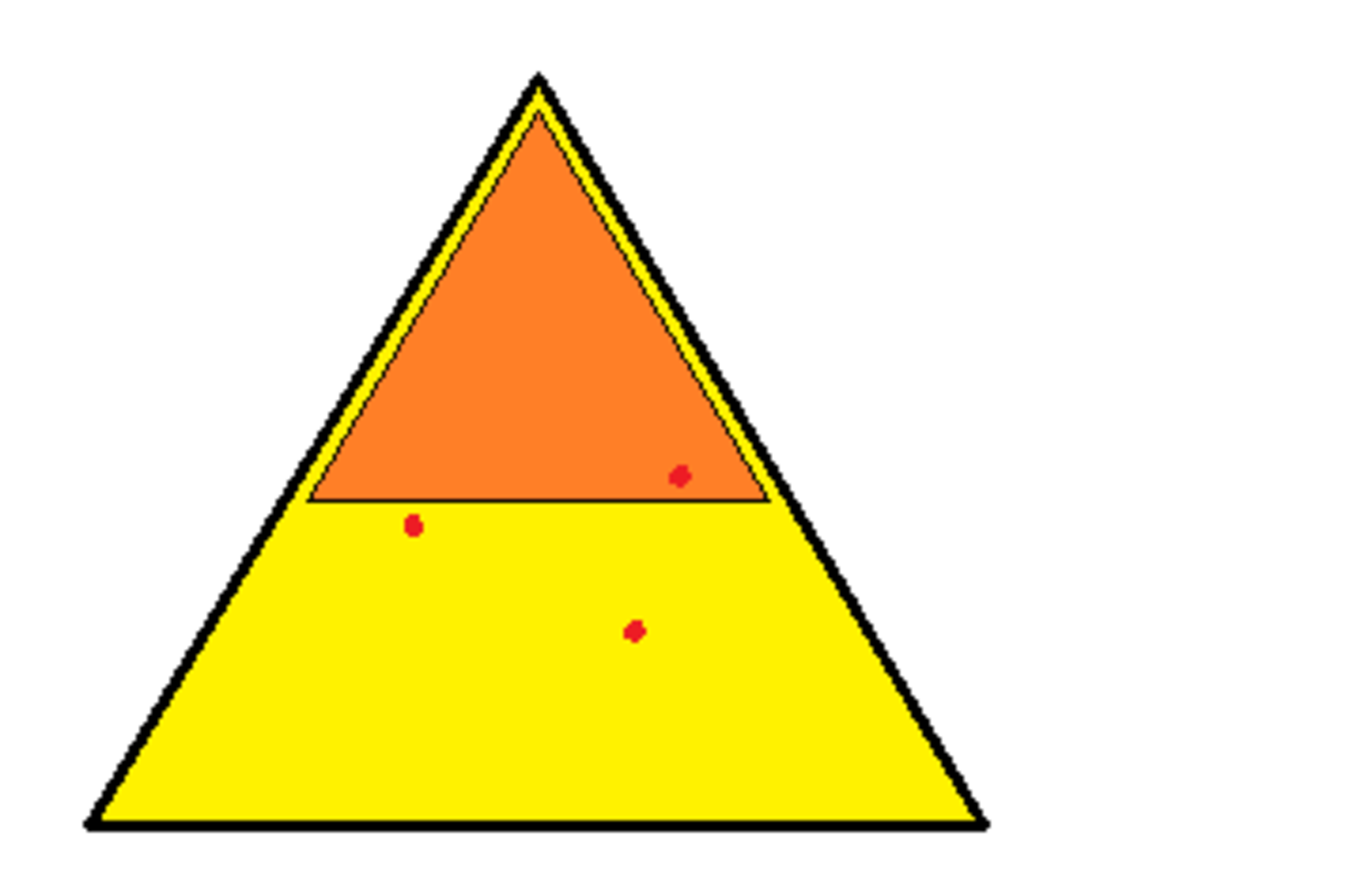
You draw three distinct dots inside an equilateral triangle that has an area of 1.
Then your friend draws the biggest equilateral triangle she can inside the original triangle which contains exactly one of the three dots (with edges parallel to those of the original triangle, and oriented the same way).
With the initial three dots, you try to minimize the size of the triangle she is able to draw.
If you play optimally, what is the area of the largest triangle she will be able to draw containing exactly one of the three dots?
Give your answer to 3 decimal places.
Assume that the dots are allowed to share the same or coordinate, but not both.
Bonus: Can you generalize this for dots?
The answer is 0.111.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.

You can keep her triangles to within 9 1 of the total area by putting all three points right in the middle of the big triangle in the shape of three vertices of an upside down regular triangle, (i.e. right where the vertices of the three green triangles meet in the picture below, one at each vertex) and then let the spacing between them, Δ → 0 .
Also, she can always get at least 9 1 of the area by choosing one of the three triangles shown here:
(and let all spaces and gaps go to zero!)
If one of them contains only 1 dot, then she is done.... 9 1 of the area. Otherwise she can "expand out" a triangle that contains no dots by pulling one side out (keeping the triangle regular) until it contains one dot. Once it does, you are done. (If it so happens that it suddenly contains more than one dot, then choose the other side that's not against the edge of the large triangle). If. in the rare case that you hit three dots all at once, then once you do can make a triangle containing one of the triangles on the end of the three, and the edge that's farthest away from it to form a triangle with an area greater than 9 1 .
And, since the area of the triangle is 1 , then the area of the biggest triangle she can draw will be 9 1 = 0 . 1 1 1 when rounded to 3 decimal places.