3 squares + 2 triangles
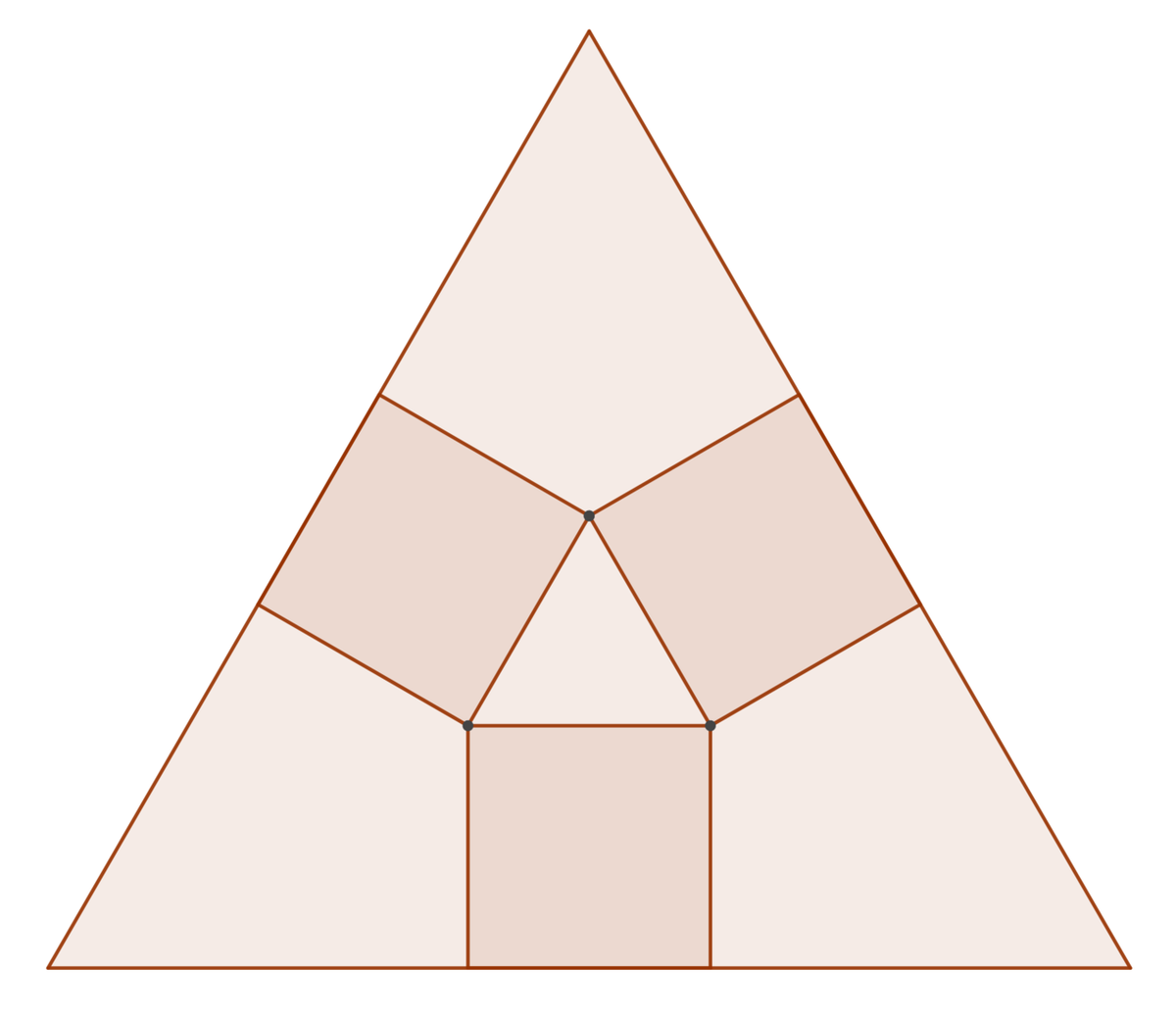
The figure shows congruent three squares aligned with the sides of an equilateral triangle. The inner sides of the squares form another equilateral triangle. If the ratio of the area of the small triangle to the area of the large triangle is t , submit ⌊ 1 0 6 t ⌋ .
The answer is 50180.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Log in to reply
Thanks. I have corrected it. Please try not to use so much "!" in English. It means that you are shouting at me to "Correct it!" like a teach to a small child.
Log in to reply
A fair complaint. Vijay's demand was made rudely.
Sorry Chew.
Log in to reply
@Vijay Simha – It is alright. I was not complaining but just to let you know. It is not sensitive in ohter languages such as Chinese but not English.
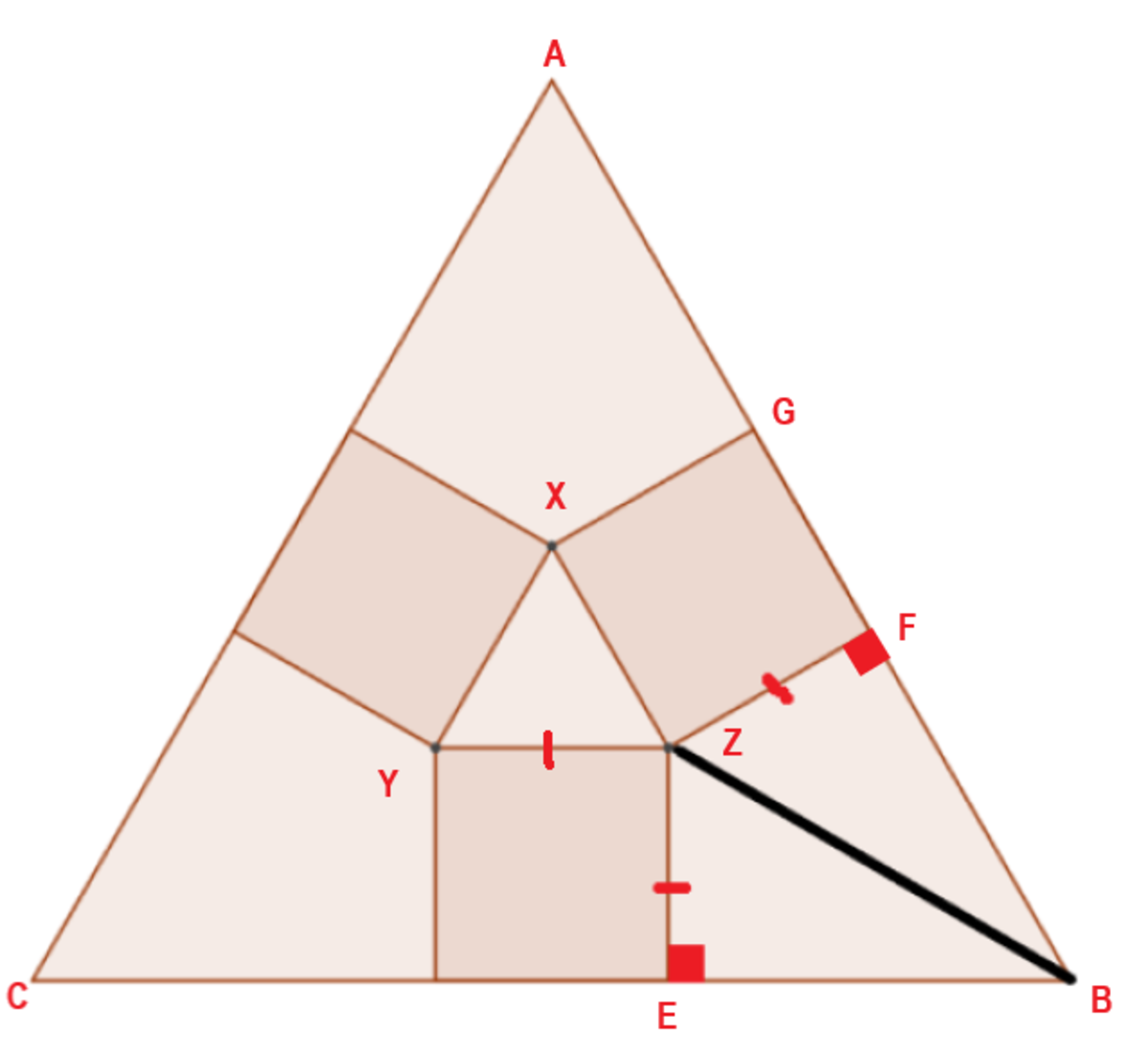 Let length of each side of
△
X
Y
Z
be equal to
a
. Since the three squares share a common side with
△
X
Y
Z
, the length of each side the squares is also
a
.
Let length of each side of
△
X
Y
Z
be equal to
a
. Since the three squares share a common side with
△
X
Y
Z
, the length of each side the squares is also
a
.
Notice that Z E = Z F ∠ Z E B = Z F B = 9 0 ∘ ⟹ △ B E Z ≅ △ B F Z So we have ∠ Z B E = ∠ Z B F = 2 ∠ B = 3 0 ∘ In △ B F Z , tan 3 0 ∘ = B F Z F = B F a ⟹ B F = a 3 The length of each side of △ A B C is A B = A G + G F + B F = a 3 + a + a 3 = a ( 2 3 + 1 ) Therefore, t = [ △ A B C ] [ △ X Y Z ] = 4 3 ⋅ A B 2 4 3 ⋅ X Y 2 = ( a ( 2 3 + 1 ) a ) 2 = ( 2 3 + 1 ) 2 1 ⟹ t ≈ 0 . 0 5 0 1 8 0 1 3 ⟹ ⌊ 1 0 6 ⋅ t ⌋ = 5 0 1 8 0
Let the side length of the small equilateral triangle and square be 1 . Joint the top vertices of the two equilateral triangles with a line. Then we note that the side length of the large equilateral triangle is 1 + 2 3 . Since the area of of a same shaped figure is directly promotional to the square of linear dimension, the ratio of the area of the small equilateral triangle to the area of the large equilateral triangle is:
t = Δ l a r g e Δ s m a l l = ( 1 + 2 3 ) 2 1 2 = 1 3 + 4 3 1 ≈ 0 . 0 5 0 1 8 0 1 3 9 ⟹ ⌊ 1 0 6 t ⌋ = 5 0 1 8 0