3 × 3 × 3 Magic Cube
A 3 × 3 × 3 magic cube is a three-dimensional array of the consecutive integers 1 through 2 7 , with the special property that the sum along any row, any column, any pillar, or any of the four space diagonals is equal to the same number.
How many different 3 × 3 × 3 magic cubes are there?
Note: Rotations of a certain solution are considered the same solution and therefore not counted.
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
"A quick computer search of the 4 ! × ( 4 2 6 ) = 3 5 8 8 0 0 possible choices for q , r , s , t yields a total of 1 9 2 possible magic cubes."
Yes!
Log in to reply
Well yes, a four-line piece of Mathematica code is pretty quick.
Taking the basis element a into consideration explains your hunch, that the middle number is a third of the magic number.
Log in to reply
It turns out that I didn't need to rely on that hunch although that's what I did in my first try at this problem. Solving the system of 31 linear equations takes care of that.
Looking at the possible values of the centers of the faces was a fast way of determining that the number can't be greater than 4, if we allow chiralty. I inititally didn't count the 192 possible cases.
Still, your solution, as with all of your other solutions, is highly interesting and pretty thorough.
Log in to reply
@Michael Mendrin – It is possible to get the “centre equals magic number over three” result more simply. Consider adding all four diagonals, plus the two central lines, top and bottom. Sum is 8 M . This is equal to all the top squares, plus all the bottom squares, plus the vertical middle line, plus three times the central cube, which adds to 7 M + 3 C . Thus 3 C = M .
Log in to reply
@Mark Hennings – The 31 linear equations overdetermines the solutions, being that there's only 27 unknowns. While I didn't see the approach you've suggested in determing the value of the center, it does make sense. There's going to be some degeneracy here, if solutions exist at all.
Log in to reply
@Michael Mendrin – We are looking at a 3D version of the normal proof for magic squares...
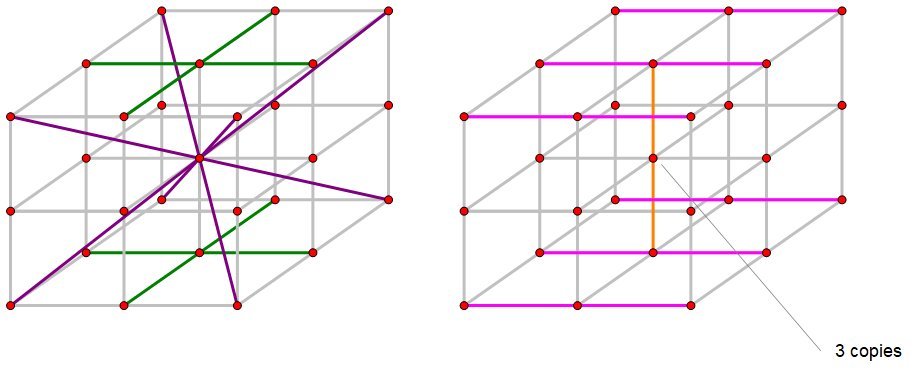
Look at the left-hand picture. Add up the numbers in the four diagonals (purple), plus the numbers in the two central lines, top and bottom (green). This gives us a total of 8 copies of the magic number M . The total is 8 M .
Look at the same sum in the right-hand picture. We have the three rows in the top layer, plus the three rows in the bottom layer (pink), plus the central pillar (orange), plus three copies of the central number. The total is 7 M + 3 C , where C is the central number.
Thus M = 3 C .
Out of interest, do you think I have decoded Prince's offering?
Log in to reply
@Mark Hennings – In regards to Prince's explanation, I don't know! The problem is, I am not even sure what he is talking about. But, assuming that he only means to swap the outside faces, then such a move gets you the chiral opposite, which means if other faces were to be swapped instead, then it's the same chiral opposite. In other words, he's only accounted for 2 out of 8 possible. Your explanation of doing a double swap and showing it to be the same effect as doing a rotation, is saying the same thing.
I think an easy way to illustrate this is to use a mirror, and look where the numbers are in it. Never mind that the numbers themselves are reversed. Come to think about this, this could be an excellent way to explain the "paradox" why when we look ourselves in a mirror, it appears that only right and left are reversed, and we never speak of our top and bottom being reversed.
As for resolving those 31 equations, well, lots of ways to approach that one. But your method for resolving the center value is a good start. As I said, it makes good sense. I wonder if others will get into the comments and see it.
Sir, can you please explain how you got that dimension for the magic cube?
Log in to reply
Firstly, by taking away a suitable multiple of a , you can consider magic cubes with magic number 0 only. If we have a magic cube with magic number 0 , try putting q , r , s , t in the four corners of the bottom layer. You will find that the remainder of the numbers in the cube are uniquely determined, without redundancy.
There are 2 7 unknowns, while there are 2 7 + 4 equations that all equal to 4 2 . When that set of linear equations are solved, 2 2 of the unknowns are determined by 4 variables, while the center of the cube is 1 4 , which makes a computer search feasible. If we add the condition that all the unknowns are from 1 to 2 7 , then the only values that the center of the faces can have are
( 1 , 3 , 7 , 9 , 1 9 , 2 1 , 2 5 , 2 7 )
which means only the following pairs are possible, if the center 1 4 is included:
( 1 , 2 7 ) , ( 3 , 2 5 ) , ( 7 , 2 1 ) , ( 9 , 1 9 )
Since any magic cube uses 3 of the 4 , there are only 4 distinct magic cubes possible. However, for this problem, chirals are considered distinct, so double that to get 8 .
Note: As a check, using all possible distinct values for the 4 variables with the condition that all values are from 1 to 2 7 , there are 1 9 2 possible cases. A cube can have 2 4 ways of being rotated, and 2 chiral versions, so, given that there are only 4 distinct sets of 3 pairs described above for the magic cubes, we have 2 4 ⋅ 2 ⋅ 4 = 1 9 2 .
Can you explain "22 of the unknowns are determined by 4 variables"? Presumably these variables are linear combinations of the original unknowns? How do you know that's the case - is it because we have 4 more equations than unknowns and we know that solutions must exist? Did you determine what these 4 variables are? Thanks.
Log in to reply
As I have said elsewhere in comments to Mark Hennings, the system of 31 equations is overdetermined, so that it can and should be reduced to just 22 equations that will yield the values of 22 variables in terms of the other 4, wtih the center being determined as 14 in all cases.
It will fill out a bit of space to go through all of that, just listing the 31 equations will take up room.
There seems to be one more symmetry: you can swap 1 with 27, 2 with 26, etc. to transform any of the 4 cubes to another. So only 2 classes of solutions are non-trivially distinct. Right?
This transformation may be easier to visualize if the numbers used are -13 through 13 (with 0 at the center) instead 1 through 27. Then we can simply reverse the sign of each number.
FIRST CONSIDER THE THREE PLANES red,green,blue .YOU CAN ASSEMBLE THEM (3-1)! WAYS.THEN YOU CAN UNDERSTAND THAT YOU CAN TAKE THREE PLANES LIKE THAT IN THREE WAYS.SO THE SOLUTION IS 2×2×2=8
Can you explain this further? Wouldn't switching 2 pairs of faces give the original diagram?
Log in to reply
That is a good observation. Switching two different pairs of faces will get us back the original.
Log in to reply
.. yes, a rotated version of the original. That is the meat of my comment.
No,you have to avoid only the rotation,switching two pairs you will not get the pattern by rotation.So it 's a distinct solution
The green plane with 14 at the center cannot be anywhere else. The center has to be 14.
If I understand your argument, you are saying that, given a magic cube, you could swap the top and bottom slices, or swap the front and back slices, or swap the left and right slices. Each of these operations gives you another magic cube, and you claim to get 2 × 2 × 2 cubes, choosing "swap or don't swap" for each of the three pairs of faces.
Sadly, this is not the whole story, since swapping the front and back, and then swapping the left and right, faces has the same effect as rotating the cube through 1 8 0 ∘ about the axis through the midpoints of the top and bottom faces. Thus some of the eight cubes you get in this way are, in the terms of the question, the same. Since there are 8 different cubes, the consequence is that some of these 8 cannot be obtained from one of them by swapping opposite faces.
The answer is 8 which is the number of magic series for n=3 that sum to ((n^3+1)*(n/2))=42 along all allowed directions. The series A052456 is given at the following links for general value of n:
https://en.m.wikipedia.org/wiki/Magic_series
https://oeis.org/A052456
The problem with this is that the magic series does not tell you the number of magic cubes of any particular dimension. There are 4 different 3 × 3 × 3 magic cubes to within reflection and rotation (so 8 to within reflection), and 5 8 different 3 × 3 × 3 × 3 magic tesseracts to within rotation and reflection (so 1 1 6 to within rotation). While the magic series value of 8 may match the 3D case counting reflections as distinct, the magic series term of 8 6 does not match the 4D magic tesseract count of 1 1 6 .
The vector space of real 3 × 3 × 3 magic cubes is 5 -dimensional, with basis a b c d e = ⎝ ⎛ 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ⎠ ⎞ = ⎝ ⎛ 1 − 1 0 − 1 1 0 0 0 0 − 1 1 0 1 0 − 1 0 − 1 1 0 0 0 0 − 1 1 0 1 − 1 ⎠ ⎞ = ⎝ ⎛ 0 0 0 − 1 1 0 1 − 1 0 0 − 1 1 1 0 − 1 − 1 1 0 0 1 − 1 0 0 1 0 0 0 ⎠ ⎞ = ⎝ ⎛ 0 0 0 0 1 − 1 0 − 1 1 1 − 1 0 − 1 0 1 0 1 − 1 − 1 1 0 1 − 1 0 0 0 0 ⎠ ⎞ = ⎝ ⎛ 0 − 1 1 0 1 − 1 0 0 0 0 1 − 1 − 1 0 1 1 − 1 0 0 0 0 1 − 1 0 − 1 1 0 ⎠ ⎞ where each successive 3 × 3 block represents the numbers in the bottom, middle and top layer of the cube, respectively. Note that the magic number of the cube p a + q b + r c + s d + t e is 3 p , and its central number is p . We want to know how many ways there are of choosing p , q , r , s , t such that the resulting magic cube only contains the integers from 1 to 2 7 . The magic number of such cubes is 9 1 × 2 1 × 2 7 × 2 8 = 4 2 , so it is clear that p must be equal to 1 4 . Then q , r , s , t must be distinct integers chosen from ± 1 , ± 2 , … , ± 1 3 . A quick computer search of the 4 ! × ( 4 2 6 ) = 3 5 8 8 0 0 possible choices for q , r , s , t yields a total of 1 9 2 possible magic cubes. Since the rotation group of the cube has order 2 4 , this means that there are 1 9 2 ÷ 2 4 = 8 different magic cubes, to within rotation.
This result is more normally expressed by identifying cubes that can be obtained from each other by reflection, too. This would mean that there were fundamentally only 4 different magic cubes.
The eight different cubes are given by the choices ( q , r , s , t ) = ( − 1 3 , 4 , − 1 2 , 1 0 ) , ( − 1 2 , 2 , − 1 1 , 8 ) , ( − 1 0 , − 2 , − 7 , 6 ) , ( − 8 , − 4 , − 6 , 5 ) , ( − 1 3 , 4 , − 1 0 , 1 2 ) , ( − 1 2 , 2 , − 8 , 1 1 ) , ( − 1 0 , − 2 , − 6 , 7 ) and ( − 8 , − 4 , − 5 , 6 ) , where the last four are the mirror images of the first four.
This result was originally proved by Hendricks in the Journal of Recreational Mathematics in 1972. I have not been able to locate a copy of the paper yet.