#30 of Sept 2015 Grade 10 CSAT (Korean SAT) Mock test
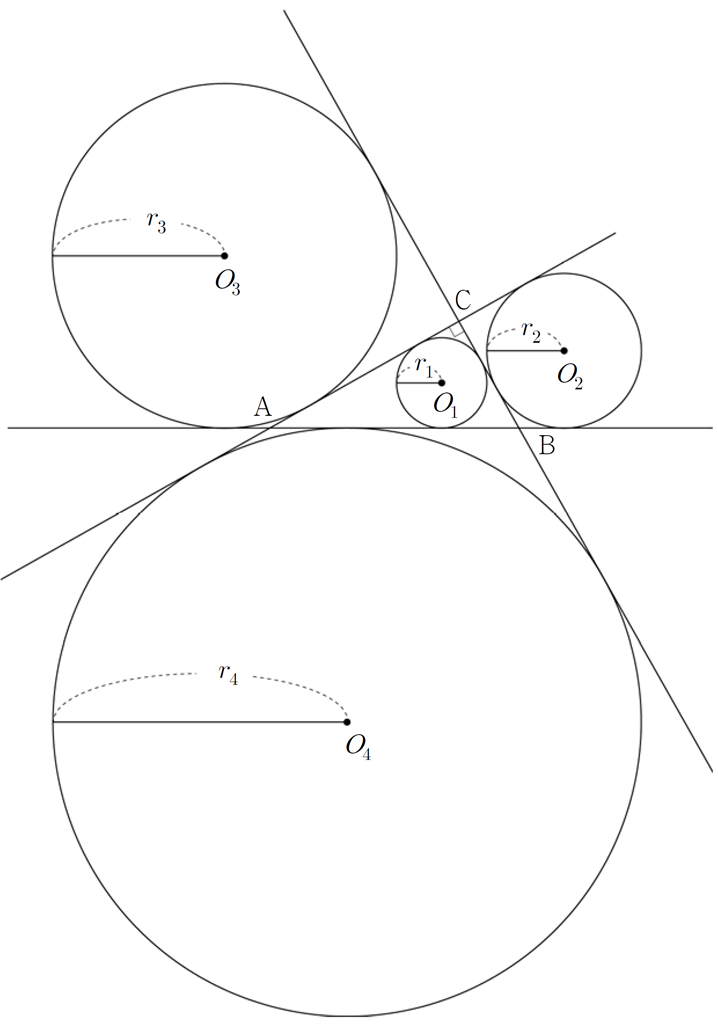
As the image above shows, a right triangle A B C has O 1 as its inscribed circle, and O 2 , O 3 , O 4 as its escribed circle. The radius of a circle O i is r i . ( i ∈ { 1 , 2 , 3 , 4 } )
Given that r 1 = 1 and that the area of triangle A B C is 2 1 5 , find the value of r 2 + r 3 + r 4 .
This problem is a part of <Grade 10 CSAT Mock test> series .
The answer is 14.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
These 3 large circles are also called excircles. There's plenty of useful formula that is relevant here.
Log in to reply
Mhm. Those are very useful. I used them once or twice on some geometry problems, and they're strikingly effective when the given information doesn't seem enough!
I guess this is wrong. How can r4 be s? I got answer as 7. Please check
Log in to reply
If you want to see why, here's an explanation.

C R = r 4 , C P = r 4 . ∴ 2 r 4 = C P + C R = A C + A P + B C + B R = a + b + A P + B R = a + b + A Q + B Q = a + b + A B = a + b + c
And therefore, r 4 = 2 a + b + c .
r 4 is indeed the half of the perimeter of △ A B C .
This is the solution of Korea Institute for Curriculum and Evaluation, formed by several college professors.
Also I got the same answer when I solved it.
Log in to reply
Thanks a lot. My bad. Is it semiperimeter only when it's right angle or general.??
Log in to reply
@Mohan Nayak – It's okay!
And yeah. It's the semiperimeter only because the opposite angle is 2 π .
I think your solution might take some time to carefully observe and answer, Exams like jee and other competitive exams conducted in india requires on readymade formulas to crack such type of questions. I appreciate for your good geometrical skill.
Log in to reply
Yah, this is #30 of the exam, the hardest one of all because in here, we don't learn geometry that seriously.
Let A B , B C , C A be c , a , b respectively.
Then by above picture, we know that ( b − r 1 ) + ( a − r 1 ) = c .
r 1 = 2 a + b − c .
Also, by above picture, we know that b + r 2 = c + ( a − r 2 ) .
r 2 = 2 a − b + c .
Using similar method with r 3 and r 4 , we get
r 3 = 2 − a + b + c ;
r 4 = 2 a + b + c .
Therefore,
r 1 + r 2 + r 3 + r 4 = a + b + c = 1 5 .
∴ r 2 + r 3 + r 4 = 1 4 .