37,53 and trapezoid
A B C D is a trapezoid with A B ∣ ∣ C D , A B = 1 0 0 0 , C D = 2 0 0 8 , D = 3 7 ° and C = 5 3 ° . If M and N are the midpoints of A B and C D respectively; then find M N .
The answer is 504.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Can you please explain how EN=1004 and EM=500 ? Thanks.
Log in to reply
since DEC is a right angled triangle, The mid point of the hypotenuse is the circumcentre. Thus, ND = NC = NE because they're the radii
Log in to reply
Thanks. Got it. I should have understood before!
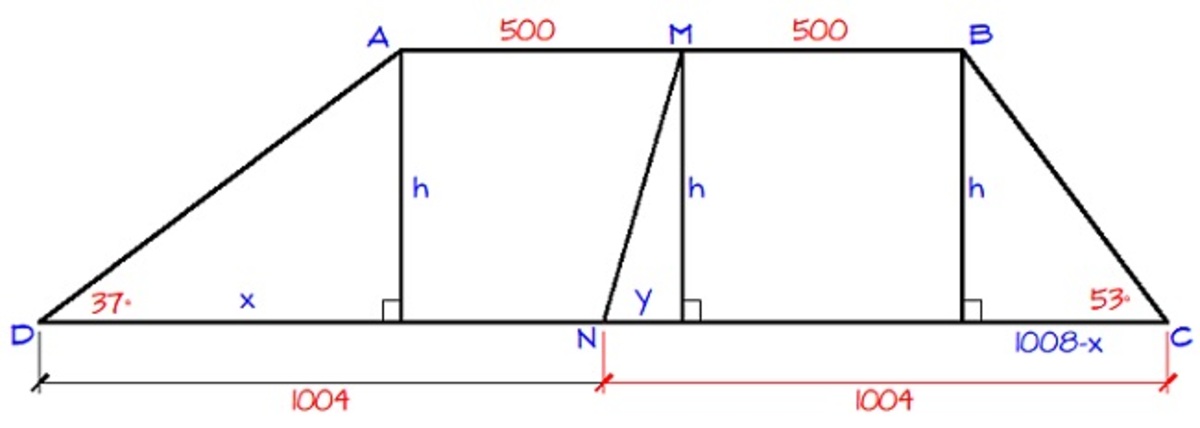
tan 3 7 = x h ⟹ h = x tan 3 7 ( 1 )
tan 5 3 = 1 0 0 8 − x h ⟹ h = ( 1 0 0 8 − x ) ( tan 5 3 ) ( 2 )
h = h Equate ( 1 ) and ( 2 ) .
x tan 3 7 = tan 5 3 ( 1 0 0 8 − x )
x ( tan 5 3 tan 3 7 ) = 1 0 0 8 − x
0 . 5 6 7 8 x = 1 0 0 8 − x
1 . 5 6 7 8 x = 1 0 0 8
x ≈ 6 4 2 . 9 4
It follows that h = ( 6 4 2 . 9 4 ) ( tan 3 7 ) ≈ 4 8 4 . 4 9
y = 1 0 0 4 − ( 1 0 0 8 − x ) − 5 0 0 = 1 0 0 4 − ( 1 0 0 8 − 4 8 4 . 4 9 ) − 5 0 0 = 1 3 8 . 9 4
By pythagorean theorem, we have
M N = ( 4 8 4 . 4 9 ) 2 + ( 1 3 8 . 9 4 ) 2 = 5 0 4
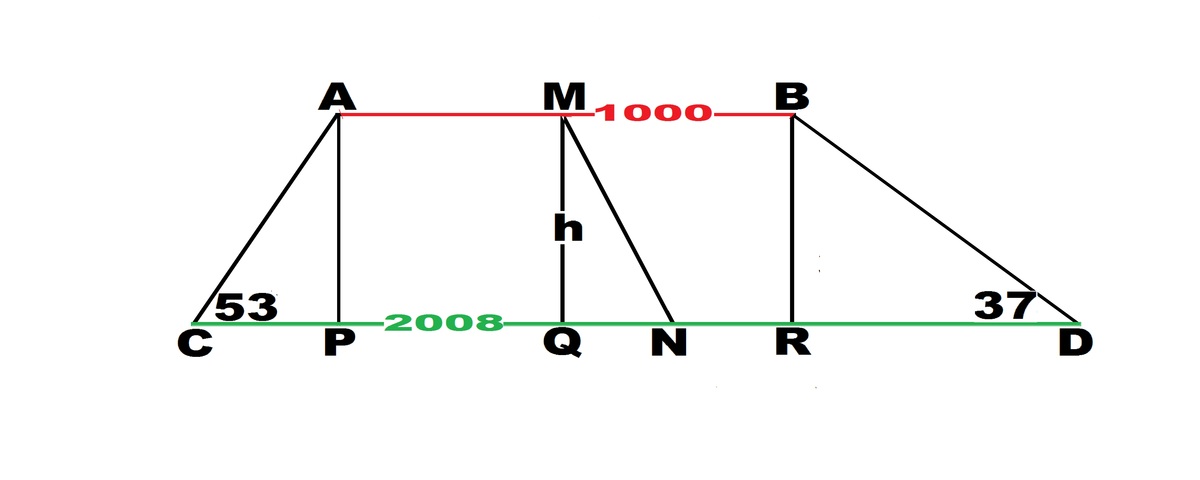
Draw perpendiculars from A, M, B, on DC with feet at P, Q, R . T h e h e i g h t h = C o t 3 7 + C o t 5 3 2 0 0 8 − 1 0 0 0 = 4 8 4 . 4 7 . C P = h ∗ C o t 5 3 = 3 6 5 . 0 7 . ∴ P N = 2 C D − C P , a n d A M = 2 A B . ∴ Q N = P N − A M = 1 3 8 . 9 3 . ⟹ M N = h 2 + Q N 2 = 5 0 3 . 9 9 6 7 5 1 8 . SINCE answer box need answer in integer, M N = 5 0 4
O
R
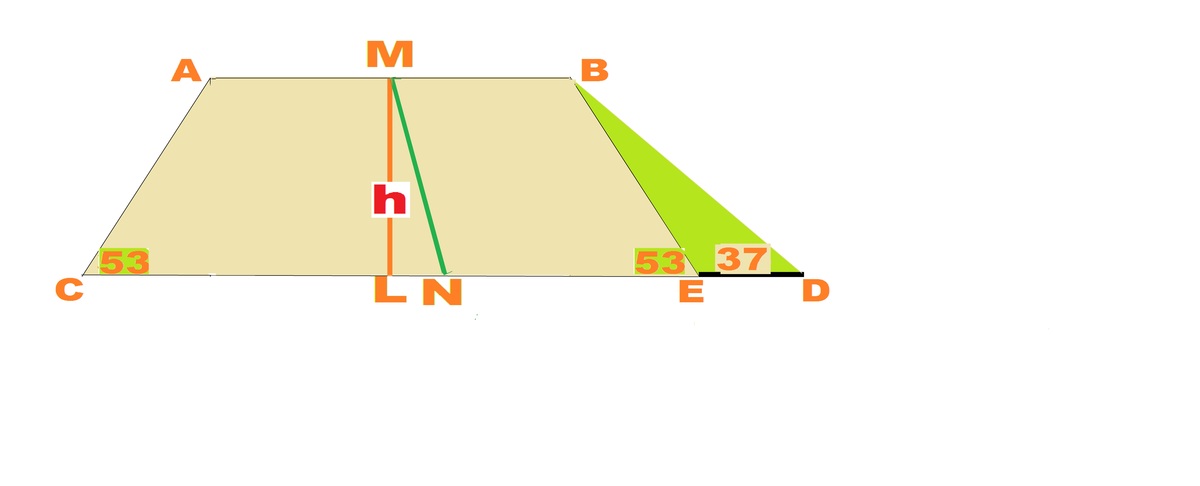
Let BEC=53 degrees. So ABEC is an isosceles trapezoid. M, L are midpoints of AB and CE. F r o m A B D C , t h e h e i g h t h = C o t 5 3 + C o t 3 7 2 0 0 8 − 1 0 0 0 = 4 8 4 . 4 7 . E D = h ∗ ( C o t 3 7 − C o t 5 3 ) Line CE, E is pulled through ED, its midpoint is pulled by 2 E D . 2 E D = L N = 1 3 8 . 9 1 9 5 . S o M N = h 2 + L N 2 = 5 0 3 . 9 9 6 7 5 1 8 .
Extend A D and B C and suppose they meet at E . E = 9 0 ° as D = 3 7 ° and C = 5 3 ° . E N = 1 0 0 4 as it is the median of triangle D E C . E M = 5 0 0 (same reason). Hence, M N = 5 0 4 .