4 Balls 4 Cells

Probability Level 4

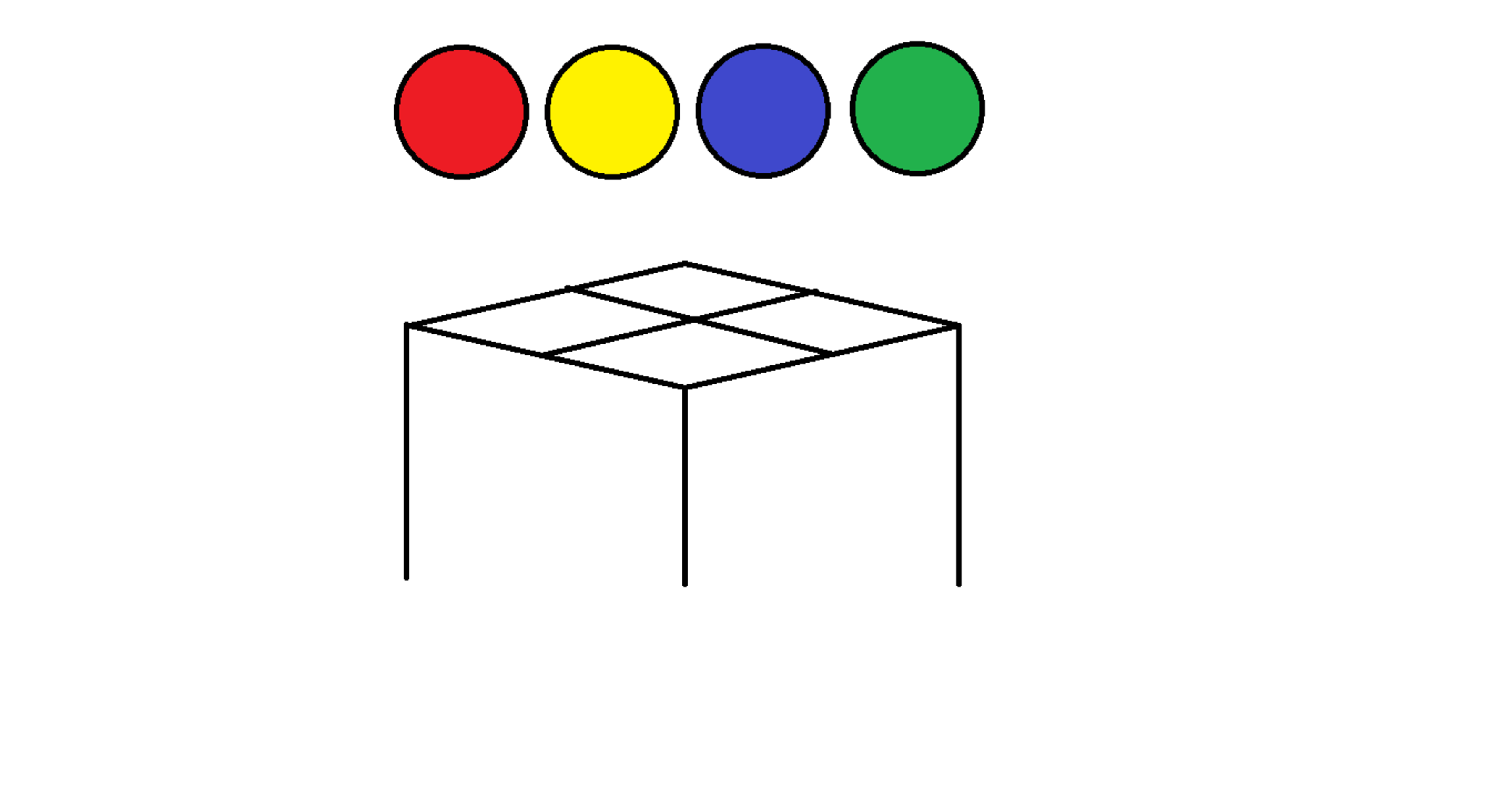
Consider the set $S$ of partitions of four differently colored balls into as many as four groups.

What is the probability that in a partition chosen randomly from $S$ , the yellow ball is grouped alone?

\dfrac{1}{5}

\dfrac{1}{2}

\dfrac{1}{6}

\dfrac{1}{4}

\dfrac{1}{3}

1 solution

Worranat Pakornrat
Mar 1, 2017

If we designate $R, B, G, Y$ as distinct elements for red, blue, green, & yellow respectively. If we desire a distinct set of yellow only, we will need to find out the partition sets of the other $3$ elements, and there are $5$ ways to arrange them:

{{R, B, G}}, {{R}, {B,G}}, {{B}, {R,G}}, {{G}, {B,R}}, {{R}, {B}, {G}}

From these $5$ arrangements, the yellow ball can be placed separately from the $3$ balls.

This partition number is also called Bell Number , and we can write the notation as:

$B_{3} = 5$ .

By adding $Y$ to join any of the $10$ sets above, we will obtain $10$ more arrangements and can calculate all possible outcomes for $4$ elements: $B_{4} = 15$

Therefore, the probability of only one yellow in one of the compartments = $\dfrac{B_{3}}{B_{4}} = \dfrac{5}{15} = \dfrac{1}{3}$ .

Nice problem and solution. At first, looking at the diagram, I was a bit confused because the partitions shown had different orientations to one another, (side-by-side or diagonally across from one another), which didn't seen consistent with them being "identical". So for my first attempt, for the purposes of counting, I considered the boxes distinct and then divided by $4$ to account for rotational symmetry. This gave an adjusted sample space of $64$ outcomes in general, $27$ of which involved the yellow ball being alone. But as $\frac{27}{64}$ wasn't one of the answer options I decided to just ignore the diagram and just focus on the text, after which I found that in a sample space of $15$ partitions, $5$ involved the yellow ball being alone.

Brian Charlesworth - 4 years, 3 months ago

Thank you and sorry for my bad graphics.

Worranat Pakornrat - 4 years, 3 months ago

I also "ignored the diagram and just focus on the text."

On the other hand, I also have the same qualms as Jon Haussmann has in the report section, do you think there's a way to improve this question?

Pi Han Goh - 4 years, 2 months ago

Jon does have a valid point, and I've made a suggested revision in a comment to his report. I'll be interested to hear what you think.

Brian Charlesworth - 4 years, 2 months ago

@Brian Charlesworth – Will this edition make any difference?

Worranat Pakornrat - 4 years, 2 months ago

Dont get this at all. IF the yellow is alone in one bin THEN there are three other choices for the others...each with 3/4 probability or 27/64 that all three other balls avoid the container that yellow is in

Greg Grapsas - 4 years, 3 months ago

That works in case of 4 different spaces, but here they are considered identical.

Worranat Pakornrat - 4 years, 3 months ago

4 Balls 4 Cells

1 solution

0 pending reports