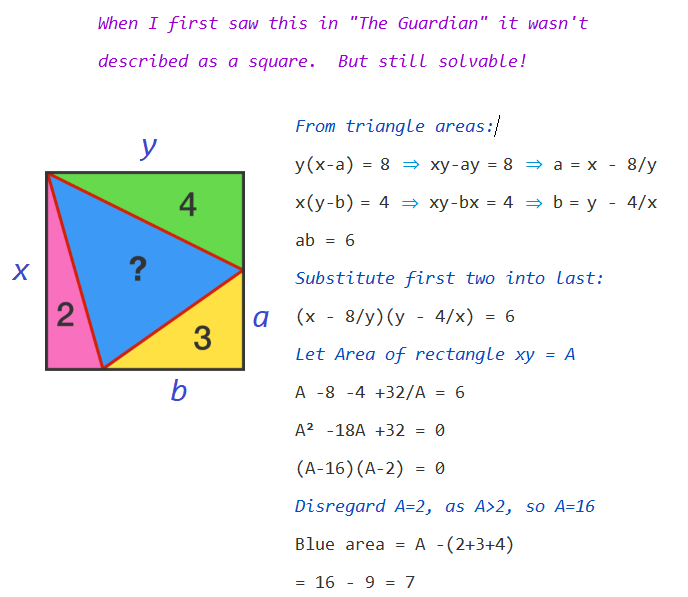
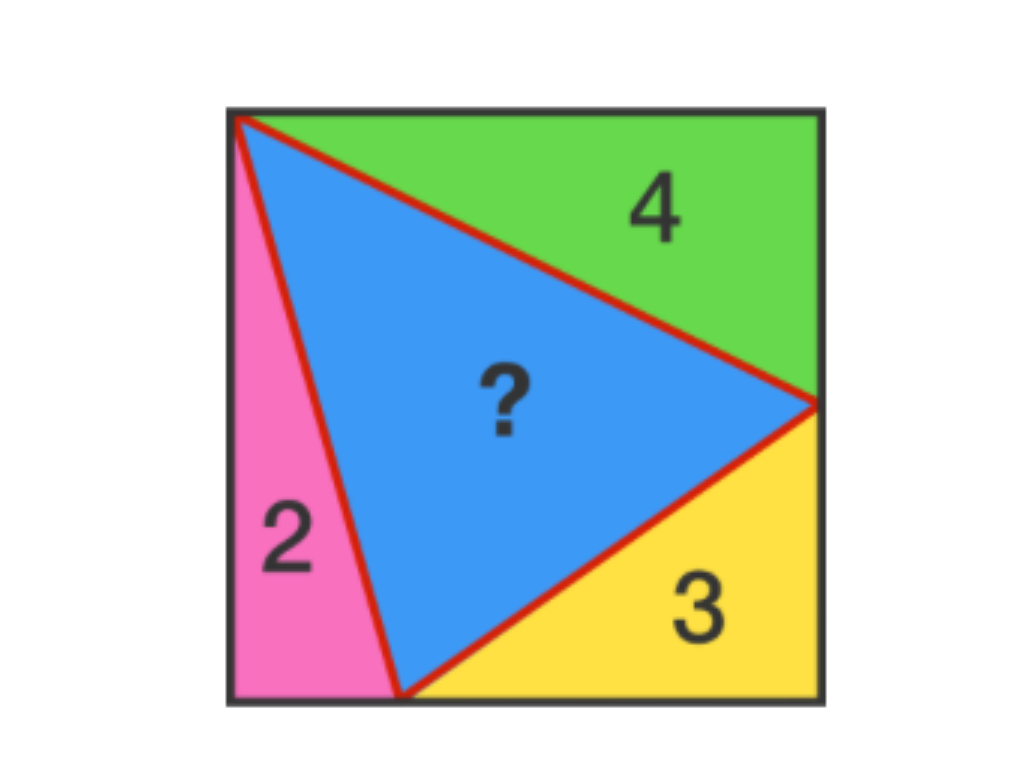
4-Colored Square
As shown, a square is partitioned into 4 colored triangles, and the number in each triangle indicates the area of that triangle.
What is the area of the blue triangle?
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
22 solutions
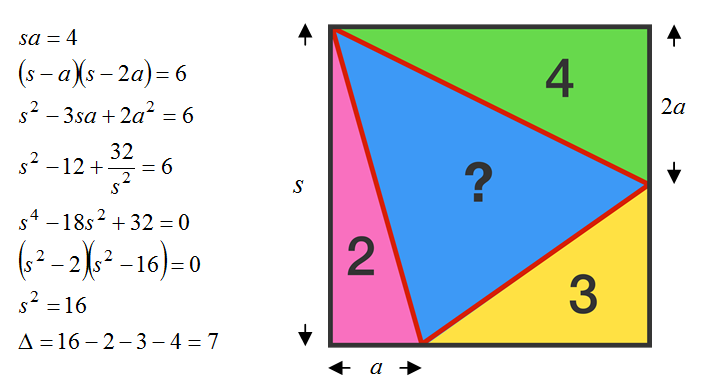
You have called the left side of the square "s" and base of left triangle "a", how did you work out that the top right corner is twice a? Thanks.
Log in to reply
Since area of green triangle above is twice that of pink triangle area, but both of those triangles have same one side - s , so from the formula of triangle = 1/2 x base x height. Assume heights of these two triangles is s , then base of green triangle has to be twice of a to have twice area. So top right corner base of green triangle becomes 2a.
cool, just two variables!!!
how does 2a^2 become 32/s^2?
Let s be the square's length, a and b be the shorter adjacent sides of the red and green triangles respective. Thus, we can set up a system of equations as followed:
2 s a = 2
2 s b = 4
2 ( s − a ) ( s − b ) = 3
Thus, s 2 − s a − s b + a b = 6 = s 2 − 4 − 8 + a b
s 2 + a b = 1 8
Then a = s 4 , and b = 2 a = s 8 ,
s 2 + a b = 1 8 = s 2 + s 2 3 2
s 4 + 3 2 = 1 8 s 2
s 4 − 1 8 s 2 + 3 2 = 0
( s 2 − 1 6 ) ( s 2 − 2 ) = 0
We know that the square's area exceeds 2 , so s 2 = 1 6 . Hence, s = 4 , a = 1 , and b = 2 .
Finally, the blue triangle's area = s 2 − 2 − 3 − 4 = 1 6 − 9 = 7 .
Checking other areas:
The red area = 2 4 × 1 = 2
The yellow area = 2 ( 4 − 1 ) ( 4 − 2 ) = 3
The green area = 2 4 × 2 = 4
The general formula for the triangle in the middle from the other three is (from the problem, let a = 2, b = 3, c = 4, and d = answer = 7): d = ( a + b + c ) 2 − 4 a c
Log in to reply
Can you explain how you arrived at this formula?
Log in to reply
Nothing unusual, just applying Worranat's method to a , b , and c instead of 2 , 3 , and 4 . I had wanted to see how frequently the middle triangle also has an integer area when the three known triangles do. (It turns out that they are pretty easy to construct.)
[ This section has been converted into a solution ]
Log in to reply
@Anton Wu – Fantastic! Thank you for sharing! ^^
Log in to reply
@Worranat Pakornrat – Thanks! And thanks also for sharing the nice problem.
Another way of looking at this problem is
 .
.
Log in to reply
How do you know that the square has side length 4?
How do you know that C is the midpoint?
Is that an assumption that you are working with? Or can you explain how you arrived at these values?
For completeness, we should verify that s = 4 , a = 1 , b = 2 do lead to a valid geometric interpretation that is described in the problem.
For example, the algebraic system could also be satisfied by s = − 4 , a = − 1 , b = − 2 , but of course that doesn't lead to a valid geometric interpretation.
Log in to reply
should be s = -4 or x = -4, not s = -2.
Suppose x is the side length of the square, y is the other leg of the triangle with area a , and z is the other leg of the triangle with area c (thus, the triangle with area b has legs ( x − y ) and ( x − z ) ). Then we have: x y = 2 a , x z = 2 c , ( x − y ) ( x − z ) = x 2 − x y − x z + y z = 2 b Dividing the first two equations gives z = a c y , and substituting the first two into the third equation gives x 2 + y z = 2 ( a + b + c ) . Thus: x 2 + a c y 2 = 2 ( a + b + c ) Now from x y = 2 a we get: a c x 2 y 2 = 4 a c So x 2 and a c y 2 are two numbers for which we know both their sum and product, so using the quadratic formula: x 2 , a c y 2 = 2 2 ( a + b + c ) ± 4 ( a + b + c ) 2 − 4 ⋅ 4 a c = ( a + b + c ) ± ( a + b + c ) 2 − 4 a c Since x 2 > y 2 and x 2 > z 2 , while a c y 2 is less than one of y 2 and z 2 (depending on whether c > a ), to find x 2 we must take the positive square root: x 2 = ( a + b + c ) + ( a + b + c ) 2 − 4 a c Finally, x 2 is the area of the entire square, so subtracting out the known triangles, we are left with: d = x 2 − a − b − c = ( a + b + c ) 2 − 4 a c as claimed.
@Anton Wu , we really liked your comment, and have converted it into a solution. If you subscribe to this solution, you will receive notifications about future comments.
this is wrong though the answer is root 7
Way too complicated!!
What if it's a rectangle instead of a square, does that change the solution? Show me :-)
Thinking outside the box, I assumed the hypotenuse of Area 4 goes from corner to middle of the right side of the square. From that middle point, mentally draw a horizontal line to the middle point of the left side of the square, the two triangles both have areas of 4 each (8). By symmetry, the bottom half of the square also has an area of 8, making the whole square area of 16 sq.u. Take away the 3 triangles (areas 2,3 and 4) -->16 - (2+3+4) = 16 - 9 = 7, which is the area of the blue triangle :-)
I tried to do it algebraically but I thought I wasn't thinking outside the box, voila :-)
How can you "assume" it is the mid point? Must it be so?
Red triangle has width = (a), and height = (4/a), yellow triangle has width =(b), and height =(6/b),
Green triangle has width = a+b, and height =8/(a+b).
Area Blue = (4/a)(a+b) – 9., The side of a squares are equal, so 4/a = 8/(a+b) + 6/b, This equations can be changed to 3a^2 + 5ab – 2b^2 = 0, or (a+2b)(3a - b) = 0, so b=3a.
Area Blue = 7
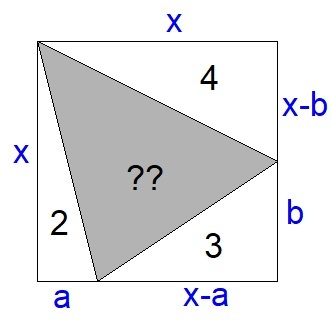 Consider my diagram. Let
x
be side length of the square.
Consider my diagram. Let
x
be side length of the square.
2 = 2 1 a x ⟹ 4 = a x ⟹ a = x 4 ( 1 )
3 = 2 1 ( x − a ) ( b ) ⟹ 6 = x b − a b ( 2 )
4 = 2 1 ( x ) ( x − b ) ⟹ 8 = x 2 − x b ( 3 )
Substituting ( 1 ) in ( 2 ) , we get b = x − x 4 6 ( 4 )
Substituting ( 4 ) in ( 3 ) , we get x 4 − 1 8 x 2 + 3 2 = 0
Let y = x 2 and y 2 = x 4 . We have y 2 − 1 8 y + 3 2 = 0
By factoring we get
( y − 2 ) ( y − 1 6 ) = 0
y = 2 and y = 1 6
y = 2 is rejected, therefore, the area of the square is x 2 = y = 1 6 .
Hence, the unknown area is 1 6 − 2 − 3 − 4 = 7
I have read all the solutions but I came up with a very simple method of my own! It is done step by step.
1) Firstly let's find the area of the square.
Without further consequences, we can find that the length of the sides is 4 cm. To find the area of the square we can square it:
4 2 = 1 6
So it is 16 c m 2
2)Now sum up the areas of the other triangles
2 + 3 + 4 = 9
3)To find the area of blue triangle, subtract 9 from 16.
1 6 − 9 = 7
So our final answer is
= 7 c m 2
How did you work out that the length of the square side is 4? The 4 is supposed to be the area of the top right triangle.
Log in to reply
I'd like to know also.
I like your approach the most but you seem to skip the most important part of how you found the sides were equal to 4. All of the other solutions were very long winded and unnecessarily complex. I blame it on common core. Also don't add units to a problem randomly. You can solve the problem without defining the lengths as inches or meters. Other than that good try.
Area of a square = Side x Side That means that the total area of the square must be a square number. 2 + 3 + 4 = 9 (which is a square) The next nearest square is 16. 16 - 9 = 7
That's a lovely solution and got to the right answer considerably quicker than my algebraic method! ... to my mind it doesn't quite prove it, as there is nothing in the question that claims the side lengths are integers, so Side x Side could easily be a non-integer result. But points for lateral thinking!
It turns out the the answer is the same even if the original figure is a rectangle, rather than a square.
See the following diagram. Let the bottom two lengths be
a
and
b
.
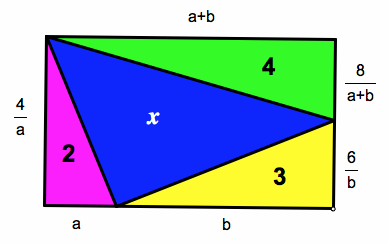
The area of the rectangle is ( a + b ) a 4 , so x = ( a + b ) a 4 − 9 = 4 a b − 5 . Thus, a b = 4 x + 5 .
The sum of the two lengths on the right is equal to the length on the left, so a + b 8 + b 6 = a 4 . Multiplying by the LCD gives 8 a b + 6 a ( a + b ) = 4 b ( a + b ) . Rearranging and dividing both sides by a 2 gives 8 a b = ( 1 + a b ) ( 4 a b − 6 ) .
Substituting a b = 4 x + 5 gives 8 ( 4 x + 5 ) = ( 1 + 4 x + 5 ) ( x − 1 ) .
Solving this equation for x gives x = 7 .
there is a square partitioned in 4 triangles. so we dont have to use formulas.
- 4 + 3 + 2 = 9
-then because the area of a square is always a perfect square the the area of the blue triangle is the area of the square minus the area of the triangles;
- 9 = 3 2 ,the next perfect square will be; 1 6 = 4 2
- 1 6 − 9 = 7
- 7
The total area is clearly 4 x the area of size marked as 4, hence total area = 16. The marked areas add up as 4+3+2=9. Hence 16-9=7.
Green area is half of the top half of the square. Therefore total area of square is 16. 16 - (2+3+4) = 7
Summary: Get area of whole square and subtract the known areas (yellow, pink, green) to get the unknown (blue) area.
Detail: Triangle area formula = Base * Height / 2 which means that the pink triangle's longest side equals 4 (it's the only way to get a resulting area of 2). So the total area of the square is 4*4 = 16 therefore the area of the blue triangle is 16 - 9 = 7.
Triangles with areas 2, 3, and 4 are right triangles with base, height b, h for 4, c, h for 2, and d, k for 3. Then by the area formula we have bh/2 = 4, ch/2 = 2, and dk/2 = 3. Now we have bh/2 + ch/2 + dk/2 = 4 + 2 + 3 = 9.
Since 2 is half of four we have ch/2 = 1/2(bh/2) = bh/4.
Since 3 is 3/4 of four we have dk/2 = 3/4(bh/2) = 3bh/8.
Now we have bh/2 + bh/4 + 3bh/8 = 4bh/8 + 2bh/8 +3bh/8 = 9bh/8 = 9, therefore bh=8.
At this point I conjectured that h=4, that being the side of the square and the heights of the triangles with areas 2 and 4. This is consistent with the apparent magnitude of the sides and the given areas of all three triangles, as a little mental math will show. That means the area of the square is 4^2=16, and the area of the blue triangle is 16 - (2+3+4) = 16 - 9 = 7.
Add the given areas of the green, pink and yellow triangles. This gives 9.
We're told the overall shape is square. i.e All four sides are equal.
As an estimate, the area of the blue triangle looks a little less than half that of the overall square.
7 is a good bet for the area of the blue triangle. This is because it would give the total area of the square as 16, meaning each side is 4. This feels about right looking again at the diagram.
Let's test the theory:
We know that the area of any triangle is half the base x height.
The green triangle has an area of 4. If we are right that the height is 4 (a complete side of the overall square) then the base must be 2. We're good so far.
If the green triangle has a base of 2, the yellow triangle must also have a base of 2 (as both bases together form a complete side of the overall square, which we believe to be 4). We're still good.
The yellow triangle must therefore have a height of 3 (because the area is 3, and the base is 2)
The pink triangle must therefore have a base of 1 (because the height is 4 and the area is 2, AND because the height of yellow triangle is 3 and each side of the overall square is 4)
Everything checks out. The square is 4 x 4 with an area of 16. The area of the blue triangle is 7.
Green triangle area is 4 square units, so the product of green triangle base and height is 8. Base is given as half of height, so base is 2 and height is 4. Height 4 is one side of a square, so area of whole figure is 4 X 4 = 16 square units. Since the given areas total 9 square units, the blue triangle is the remainder: 7 square units.
green square is a quarter of the whole area, which therefore is 16.
Thinking outside the box, and driving for a rapid solution: Let the long side of the RED triangle=S. Set/Force the short side of the RED triangle equal to "unit 1." Then we can solve for S, (the side of the SQUARE) as follows: Area RED triangle= 2=(1/2) S (1). so, S=4; Blue area=S*S-(RED+YELLOW+GREEN)=16-2-3-4=7
Assume the side length is an integer, 2+3+4=9, the next square number is 16, the extra area needed for this is 7, so guess 7 and it says I'm right :)
Let's take an educated guess. For area of top right angle triangle to be 4, one simple solution is sides of length 4 and 2. (4x2/2 = 4) For left triangle, having assumed from above that side of square is 4, other side of triangle would need to be 1. (2x2/4 =1) Therefore sides of bottom triangle would be 4-2=2 and 4-1=3. Area would be 2x3/2 = 3. As this is correct then the original guess of square side equalling 4 is correct. Therefore blue triangle area = 4x4-(2+3+4) = 7.
The triangle with area 2 has its shortest side (length a ) equal to half that of the triangle with area 4. This follows from both sharing a common base length and having areas in a 1 : 2 proportion. We can use the area of smallest triangle to define a in terms of the square's side (length s ) as follows: a = s 4 (from 2 = 2 s a )
The sides of triangle with area 3 are length s − a and s − 2 a . That triangle's area can be used to solve for the area of the square s 2 by plugging in the value of s in terms of a with the equality: 3 = ( 2 ( s − a ) ( s − 2 a ) )
6 = s 2 − 3 s a + 2 a 2
6 = s 2 − 3 s ( s 4 ) + 2 ( s 4 ) 2 (plugged in a = s 4 )
6 = s 2 − 1 2 + s 2 3 2
6 s 2 = ( s 2 ) 2 − 1 2 s 2 + 3 2
0 = ( s 2 ) 2 − 1 8 s 2 + 3 2
0 = ( s 2 − 1 6 ) ( s 2 − 2 )
s 2 = 1 6 by virtue of the area of the square ( s 2 ) having to be greater than the combined area of the labeled triangles.
Subtracting the areas of the labeled triangles from 16, yields the central triangle's area of 7 .