4 Truths, 3 Lies

Probability Level 4

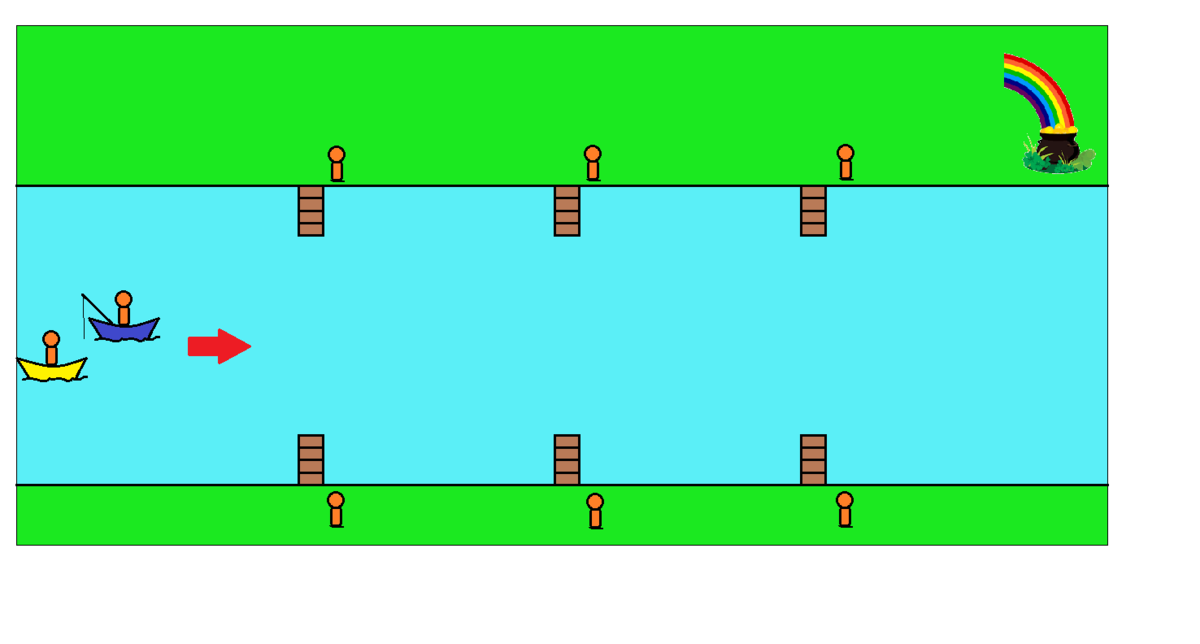
You're on the quest for the pot of gold at the rainbow's end by rowing a boat along a big river. From a distant view, you're not sure where the pot of gold is, so when you meet a nearby fisherman, you ask him, "at which side of the river bank does the rainbow end?"

The fisherman will then point towards one of the two river banks, and you'll follow his guidance downstream with thanks. Then after rowing along the river bank, you take a rest at the nearby pier before asking a villager the same question, who will then point to one of the two river banks, and you'll row your boat as his guidance once again.

There are 3 piers on each river bank, facing as 3 pairs opposite each other with one villager at every pier as shown above, so after reaching either pier, you can't row towards the opposite due to the strong current and have to row towards the next one downstream only. Also, when traveling to the river's end, you'll either succeed or fail, for you can't row against the current should you desire to cross to the opposite side.

If 4 out of these 7 guiding men are "truth-tellers", who lead you to the right place, while the other are "liars", who mistakenly get you off track, what is the probability for you to accomplish your mission?

If this probability can be expressed as $\dfrac ab$ , where $a$ and $b$ are coprime positive integers, submit $a+b$ as your answer.

The answer is 11.

2 solutions

Worranat Pakornrat
Sep 10, 2016

For better visualization, we will rewrite the guide and pot positions as a graph as shown below:

As we can see, there are $7$ available nodes for these people, and so there are $\binom{7}{4} = \dfrac{7!}{4!3!} = 35$ possible combinations.

Since there are less liars, it is easier to think of combinations to the wrong place.

First, let us suppose the far end piers both have liars (red nodes as liars; blue nodes as truth-tellers):

Clearly, with liars at both piers, the direction will be misled no matter what, and with $1$ liar left, there is $\binom{5}{1} = 5$ possible combinations. (Note that if they are both truth-tellers, the mission will also be successful no matter what.)

Second, if the liar stands at the far end pier on the right bank while the truth-teller stands opposite to him, the people at the middle piers have to guide towards the right bank and should be truth tellers:

Again, with this setting, there will be $1$ truth-teller left for the remaining $3$ nodes: $\binom{3}{1} = 3$ combinations.

Finally, for the other ways, there are $7$ possible outcomes as shown:

Therefore, there are $15$ ways to go to the wrong way and $20$ ways to find the pot of gold.

As a result, the probability to succeed = $\dfrac{20}{35} = \dfrac{4}{7}$ .

$a + b = 4 + 7 = 11$ .

The probability is 22/35 So the answer is 57

N S - 4 years, 9 months ago

I suppose that I know that there is 3 liars and 4 truths

N S - 4 years, 9 months ago

Can you show us how you've got your solution?

Worranat Pakornrat - 4 years, 9 months ago

just take in consideration this case: First three tell you to go left and the fourth tells you to go right. It is not a wise decision to neglect three because it happened that the one against them was the last.

N S - 4 years, 9 months ago

@N S – That's included in my solution. (First one in the first scenario, another in third image of third scenario)

Worranat Pakornrat - 4 years, 9 months ago

@Worranat Pakornrat – If you meet truth, truth, truth, liar. You miss the pot of gold because the last answer is wrong. The right thing to do is to make the last choice depending on all the four advices togather. Is it clear now?

N S - 4 years, 9 months ago

@N S – Clearly, that's included in my solution: blue-blue-blue-red.

Worranat Pakornrat - 4 years, 9 months ago

@Worranat Pakornrat – Yes it's included in your solution but in this case you go to side indicated by red. The right decision is not to follow what the last guide says if all three guidemen before him say the opposite.

N S - 4 years, 9 months ago

To explain this in better detail, consider all the combinations and permutations of the 4 villagers you ask, who could be truth-tellers (T) or liars (L). We don't need to worry about which side of the river you go to at each step, because the villagers are randomly allocated and just as likely to be on one side or the other. Furthermore, you are free to cross the river at each step, so all that is relevant is the status of the villagers you encounter.

Considering the combinations of T and L you may encounter:
P(4T, 0L) = 1/35 In this event P(4T, 0L AND Last villager is a T) = 1/35
P(3T, 1L) = 12/35 In this event P(3T, 1L AND Majority consensus is T) = 12/35
P(2T, 2L) = 18/35 In this event P(2T, 2L AND Last villager is a T) = 9/35
P(1T, 3L) = 4/35 In this event P(1T, 3L AND Majority consensus is L) = 4/35
P(0T, 4L) = 0 (There are only 3 liars)

So, to optimize your strategy, when all 4 villagers tell you the same thing, you know that that advice must be sound because the only way 4 of them would all say the same thing is if they were all Ts. When 3 concur and 1 differs, the odds are better that the consensus is the truth and you should heed it. P(3T, 1L) > P(3L, 1T), so you follow the majority no matter what the last one tells you. The (2T, 2L) case will give you equal counts of opposing advice, and the chances are the same that the last villager's advice is sound or not sound, so your chances are the same (9/35) no matter how you pick in that event.

Following this strategy, the probability of getting the gold is: P(win) = 1/35 + 12/35 + 9/35 = 22/35

This beats the probability of winning if you naively follow the last villagers advice by 2/35.

Michael Malione - 2 years, 2 months ago

@Michael Malione – Well, the point is the rower didn't know how many liars there are and just innocently follow their guidance. This fact of 3 liars is given merely for calculation.

Worranat Pakornrat - 2 years, 2 months ago

@Worranat Pakornrat – @Worranat Pakornrat , I believe I already addressed this point, in my earlier comment in the main thread. I was responding specifically here to your request for an illustration of the solution 22/35, which N S never gave you.

Michael Malione - 2 years, 2 months ago

This is not in keeping with the problem as stated, which says "you'll row your boat as his guidance once again." And this process is repeated with each villager you encounter, so no clever strategies are allowed.

Michael Malione - 2 years, 2 months ago

Terry Smith
Sep 15, 2016

Seems to me it all comes down to the last guy. 4/7 chance he steers you right.

You will change your answer if you just take in consideration this case: First three tell you to go left and the fourth tells you to go right. It is not a wise decision to neglect three because it happened that the one against them was the last.

N S - 4 years, 9 months ago

True enough, but the instructions explicitly say that the you always follow the guidance of each villager, even when it's not in your best interest to do so. Under this condition, it always comes down to the probability of the last villager being a truth teller, which is 4/7.

A smarter way to go would be to disregard the last villager and follow the majority consensus when all of them except for the last agree, and this would increase your probability of success by 2/35, to 22/35. However, that's not what the problem asks.

Michael Malione - 2 years, 2 months ago

I feel everything boils down to last guy as no matter what first boatman or next villagers say(truth or lie) if the last one say the truth we will reach the gold and if he lies we simply fail. so the answer should be straight away 4/7 that is the probability last guy is saying the truth.

Rishabh Mishra - 4 years, 7 months ago

4 Truths, 3 Lies

The answer is 11.

2 solutions

0 pending reports