400 followers problem!
Consider Δ A B C such that A B = 1 3 , B C = 1 4 , A C = 1 5
Let A D ⊥ B C , B E ⊥ A C , C F ⊥ A B and let H be its orthocenter
Let R ( A B C ) denote circumradius of Δ A B C
Let r 0 be inradius and r 1 , r 2 , r 3 be the exradii of Δ A B C
Then find the value of
R ( A B C ) + R ( H A B ) + R ( H B C ) + R ( H A C ) + i = 0 ∑ 3 r i
The answer is 73.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Guess I lost ! But you've got to agree that my question was easier .
Log in to reply
Yup! xD :)
Log in to reply
Well , I'll be back with a better question and then I'll challenge you :P
Log in to reply
@A Former Brilliant Member – Your 400 followers and my 500 followers problem ... :)
Log in to reply
@Nihar Mahajan – That's not possible since your followers grow exponentially and you know that ;)
Log in to reply
@A Former Brilliant Member – I will wait for you :)
@Nihar Mahajan – If I , for e.g get 400 followers , you'll be at 600-650 !
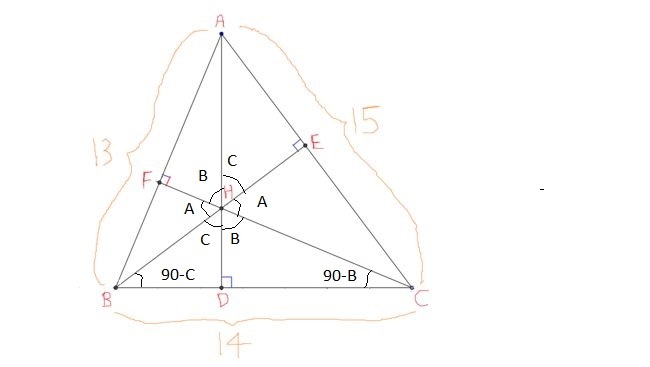
In Δ A B C , R ( Δ A B C ) = S i n A 1 4 = S i n B 1 5 = S i n C 1 3
In Δ H B C , R ( Δ H B C ) = S i n ( B + C ) 1 4
But we know A + B + C = π
Hence
R ( Δ H B C ) = S i n ( π − A ) 1 4 = S i n A 1 4 = R ( Δ A B C )
Similarily ,
R ( Δ A B C ) = R ( Δ H A C ) = R ( Δ H B A ) = R ( Δ H B C )
a r ( Δ A B C ) = 8 4 ⇒ R ( Δ A B C ) = 4 a r ( Δ A B C ) a b c
r 0 = s a r ( Δ A B C )
r 1 + r 2 + r 3 = r 0 + 4 R
Hence we have to find 8 R + 2 r = 4 × 8 4 8 × 1 3 × 1 4 × 1 5 + 2 1 2 × 8 4 = 7 3
Note: s is semiperimeter.
Nice one. I have to yet learn trigo ...... !
Let P , Q , R be the reflections of H in BC , AC , AB respectively.
m ∠ B A C = a , m ∠ A B C = b , m ∠ A C B = c a ∣ = 9 0 − a , b ∣ = 9 0 − b , c ∣ = 9 0 − c
By angle chasing we can clearly get that quadrilaterals ABPC , ABCQ , ARBC are cyclic since their opposite angles are supplementary.
⟹ R ( A B C ) = R ( B P C ) = R ( A Q C ) = R ( A R B )
Since Δ B H C ≅ Δ B P C Δ A H C ≅ Δ A Q C Δ A H B ≅ Δ A R B ⟹ R ( A B C ) = R ( H A B ) = R ( H B C ) = R ( H A C )
Area of Δ A B C = 8 4 (Using Heron's formula).Also ,
Δ A B C = 4 R product of all sides ⇒ 4 R = 8 4 2 7 3 0 = 3 2 . 5 where 'R' is circumradius of Δ A B C
Area of Δ A B C = r 0 . s ⇒ r 0 = 2 1 8 4 = 4 where 's' is the semiperimeter of the triangle.
We also have the relation r 1 + r 2 + r 3 = r 0 + 4 R
i = 0 ∑ 3 = 4 R + 2 r 0 = 3 2 . 5 + 8 = 4 0 . 5
So , R ( A B C ) + R ( H A B ) + R ( H B C ) + R ( H A C ) + i = 0 ∑ 3 r i
⇒ 4 R + 4 R + 2 r 0 = 3 2 . 5 + 4 0 . 5 = 7 3
@Azhaghu Roopesh M