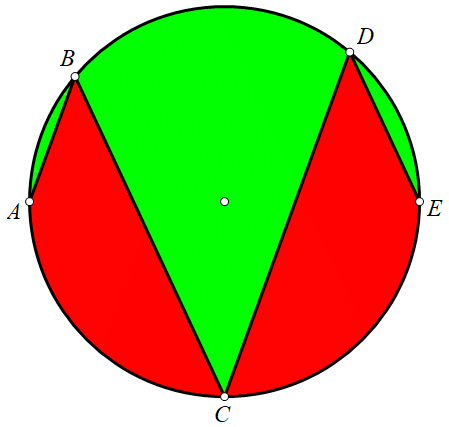
45 degrees is special

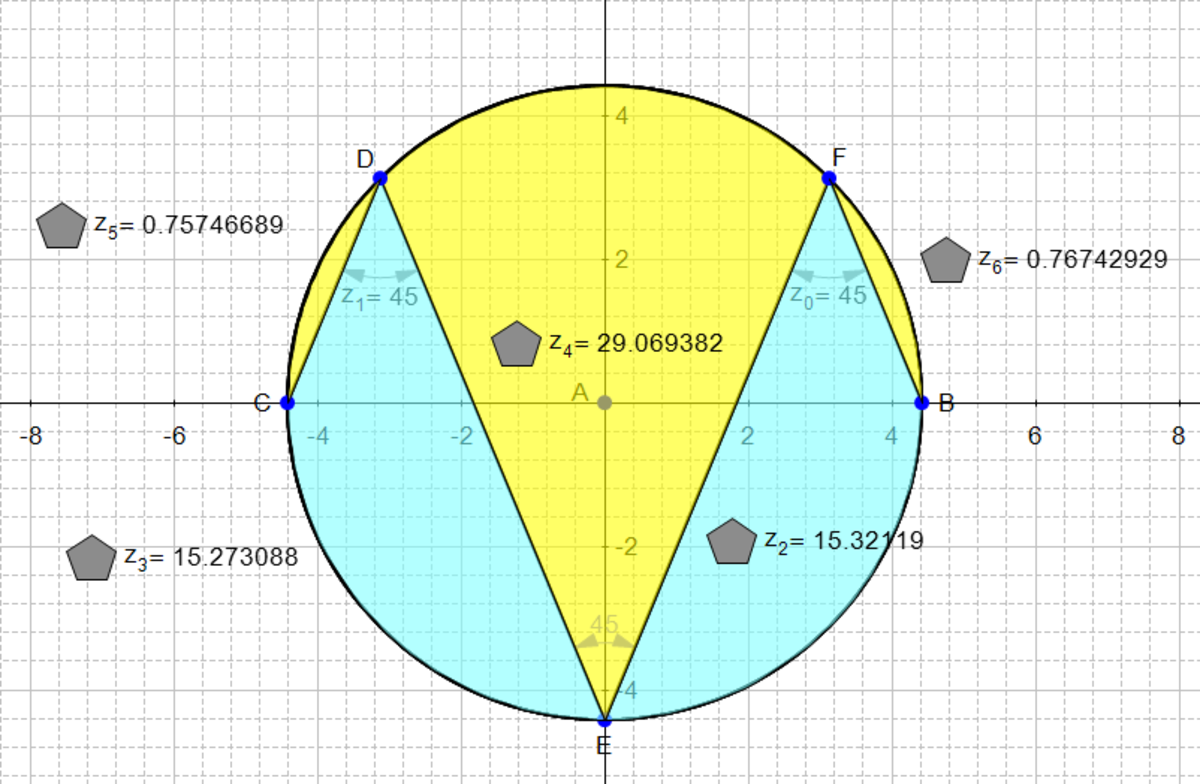
Let the center of the circle be $O$ and draw $AO$ , $BO$ , $CO$ , $DO$ , and $EO$ . Also draw a perpendicular to $AO$ from $B$ at $F$ and a perpendicular to $EO$ from $D$ at $G$ .

Since inscribed angles $\angle ABC = \angle BCD = \angle CDE = 45°$ , central angles $\angle AOC = \angle BOD = \angle COE = 90°$ . Therefore, $AE$ is a diameter. Also, by the angle sums of triangles it can be found that $\angle FBO = \angle GOD$ and $\angle FOB = \angle GDO$ , and since $BO = DO = r$ as radii of a circle, $\triangle FOB = \triangle GDO$ by ASA congruence. Therefore, $FO = GD = y$ and $BF = OG = x$ .

Both the areas of $\triangle BOC$ and $\triangle ODE$ are equal to $\frac{1}{2}ry$ , so they can be swapped and still preserve area; and both the areas of $\triangle COD$ and $\triangle ABO$ are equal to $\frac{1}{2}rx$ , so they can be swapped and still preserve area. Therefore, the green and red regions are both equivalent to areas of half a circle, so they are equal .

The large green area is composed of 1/4 of a circle + the area of 2 congruent triangles having 2 sides = radius and an included angle of 135. Therefore the large green area is r^2 {pi/4 + sqrt(2)/2}. The small green areas are each a sector with central angle of 45 degrees less a triangle with 2 sides = radius and an included angle of 45 degrees = r^2 {pi/4 - sqrt(2)/2}. Combining these terms, the green area is given by pi*r^2/2, which is 1/2 of the circle, so the areas are equal.