8 Yellow Angles

Geometry Level 1

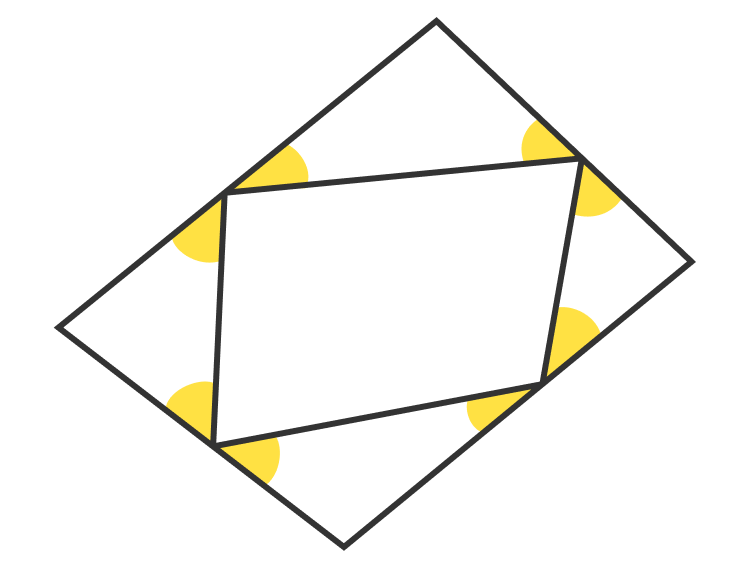
What is the sum of all 8 yellow angles?

180^\circ

360^\circ

270^\circ

540 ^ \circ

450 ^ \circ

6 solutions

Guillermo Templado
Jan 27, 2017

The sum of the interior angles in a convex or a concave quadrilateral is $360º$ . This implies that :

$\boxed{1.-}$ the sum of all 8 yellow angles is: (Looking at the external convex quadrilateral(and 4 triangles)) $180º \cdot 4 - 360º = 720º - 360º = 360º$

$\boxed{2.-}$ the sum of all 8 yellow angles is: (Looking at the internal convex quadrilateral( and 4 segments)) $180º \cdot 4 - 360º = 720º - 360º = 360º$

$\boxed{3.-}$ the sum of all 8 yellow angles is (looking at the internal convex quadrilateral) the sum of the exterior angles of this quadrilateral, i.e, $360º$

PS.- Does someone want the proof: The sume of the interior angles in a convex or a concave quadrilateral is 360º? He/she can asks to me

I want to learn the proof.

Soha Farhin Pine Pine - 4 years, 4 months ago

Don't worry, Here we are going... Take the concave or convexe quadrilateral and Draw a diagonal between two opposite vertices, then the concave or convexe quadrilateral is splitted in two triangles which sum of inner angles is 180º.. Look at this, sorry it's in Spanish . I hope you can understand it. If you don't understand it, tell me and I'll continue trying to teach the proof.

Guillermo Templado - 4 years, 4 months ago

I really appreciate your effort, but I think it would be best if you posted a detailed proof in your answer for people like me.

Soha Farhin Pine Pine - 4 years, 4 months ago

@Soha Farhin Pine Pine – Ok, give me one or two days, please... See my previous link again,without any sound please.

P. S.- I'll write the proof, but I need one or two days...

Guillermo Templado - 4 years, 4 months ago

@Guillermo Templado – It's OK. It was just a suggestion. You don't need to painstakingly demonstrate the reasoning behind the implication, if it kills your time and energy.

Soha Farhin Pine Pine - 4 years, 4 months ago

@Soha Farhin Pine Pine – Don't worry, I'm looking for a link, if I don't find a link with the proof I'll write it. Be calm... I'll do it... I have found this: here is the proof

P.S.- I hope you like it. The basic idea is there

Guillermo Templado - 4 years, 4 months ago

@Guillermo Templado – I like questions, because if you don't get one thing, or you can't understand something, or it's difficult for you, asking you can get to understand it..little by little, of course. For example, if you ask what is the Jacobian matrix of a differentiable function defined in $\mathbb{R}^n$ , you are not going to understand it, if you don't ask, study preliminary knowledge,etc. In Spain we say: Preguntando se llega a Roma... Possible translation: Asking to arrive in Rome ...

Guillermo Templado - 4 years, 4 months ago

It is a well-known fact that Sum of angles in a n-gon is $(n-2) \times 180 ^ \circ$ . This is often shown by triangulating the polygon with diagonals.

Chung Kevin - 4 years, 4 months ago

Yes, it's like this, due to triangulation... Can someone show why the sum of interior angles of a triangle is 180 º (in the Euclidean plane $\mathbb{R}^2$ )? This question is the bonus .... :)

Guillermo Templado - 4 years, 4 months ago

@Guillermo Templado – 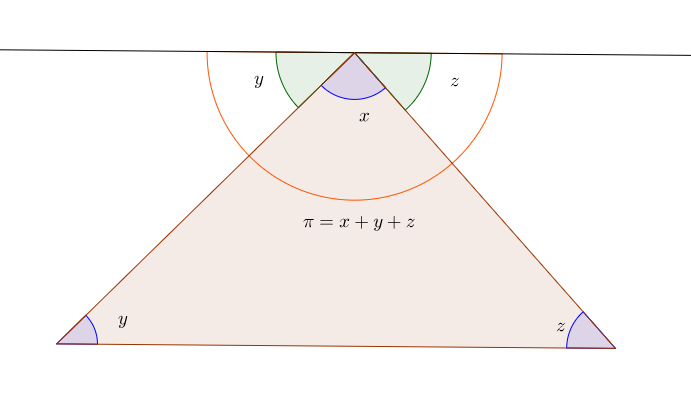Here's a proof without words as you would like it.

Tapas Mazumdar - 4 years, 4 months ago

@Tapas Mazumdar – Yes, that's exactly what I had in my mind, thank you very much Tapas Mazumdar

Guillermo Templado - 4 years, 4 months ago

@Guillermo Templado – So, what's my bonus?! :P

Tapas Mazumdar - 4 years, 4 months ago

@Tapas Mazumdar – I don't know... Maybe, other question? would you like it? The question is this: Postulate 5º Euclidean axiom: In a Euclidean plane, Given two points $A$ , $B$ , and a point $C$ , not underlying in the line $AB$ , then there exists one and only one line containing $C$ parallel to $AB$ . (Imagine this axiom in $\mathbb{R}^2$ )Then this 5º Postulate Euclidean axiom in $\mathbb{R}^2$ is equivalent to the sum of angles of any triangle in the Euclidean plane $\mathbb{R}^2$ is $\pi = 180 º$ ?

Guillermo Templado - 4 years, 4 months ago

@Guillermo Templado – I learnt about this axiom in school. This postulate was the base of how I proved the angle sum of the triangle above. To assume that there's only one parallel line parallel to one side and passing through the vertex opposite to the side. I guess if we are able to justify the angle sum result based on this postulate then the same could be justified for our postulate as well. Don't know if this works or not, but sometimes you have to make some assumptions and derive results that validate your assumptions. My final word is : Yes, maybe.

Tapas Mazumdar - 4 years, 4 months ago

@Tapas Mazumdar – Good start, you have proved one implication of this question, I advice you for the another implication reductio ad absurdum, nevertheless, we are free, so... don't listen too much to me...

Guillermo Templado - 4 years, 4 months ago

@Guillermo Templado – REDUCTIO AD ABSURDUM! Never knew that existed before this. I believe that philosophy and common sense are explicitly great tools that separate us from machines.

On the topic of axioms, my favorite one would be this conjecture (supposedly axiom):

Every even integer greater than 2 can be expressed as the sum of two primes.

( Christian Goldbach, 1742 )

What about you?

Tapas Mazumdar - 4 years, 4 months ago

@Tapas Mazumdar –

Every even integer greater than 2 can be expressed as the sum of two primes.

(Christian Goldbach, 1742) is a conjecture.

One conjecture is not an axiom, one conjecture is a proposition,postulate what it's not known whether it's true or false... For example, Fermat's last theorem was a conjecture until Andrew Wiles proved it was true. Other example, Riemann Hypothesis is, right now, a conjecture because it is not known whether it's true or false... I don't have a favourite conjecture... There are 7 millenium problems . Every one of these problems is a special problem for me.

Guillermo Templado - 4 years, 4 months ago

@Guillermo Templado – There is a movie talking about Goldbach's conjecture. It's La habitación de Fermat, Fermat's room

Guillermo Templado - 4 years, 4 months ago

@Tapas Mazumdar – I love that proof for a triangle :)

There's also the pictorial argument that the sum of exterior angles in an (convex) n-gon is $360 ^ \circ$ , which allows us to establish that the sum of interior angles in an n-gon is $(n-2) \times 180^ \circ$ .

Chung Kevin - 4 years, 4 months ago

@Chung Kevin – 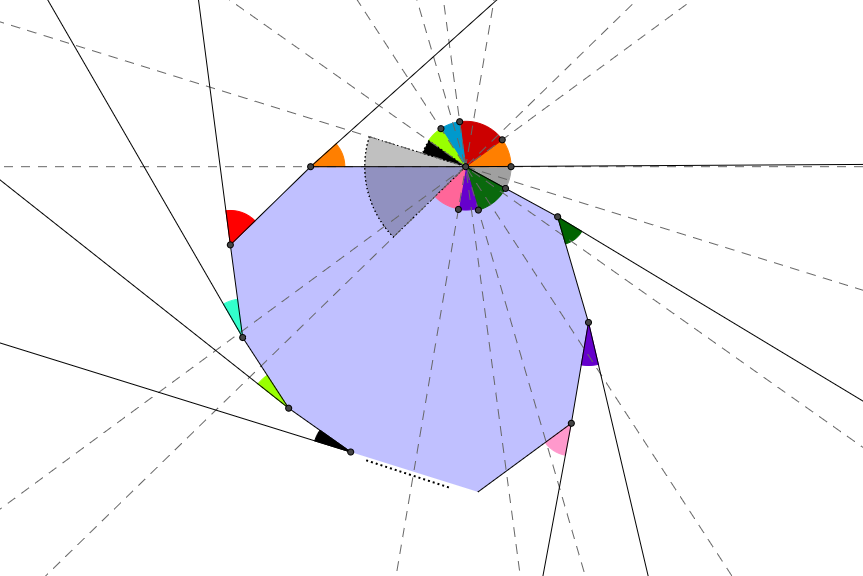How about this?!

Tapas Mazumdar - 4 years, 4 months ago

@Tapas Mazumdar – Interesting. I like it!!... I'll check it out later, however I think there is an easier form to prove it... what is this form?

Guillermo Templado - 4 years, 4 months ago

@Guillermo Templado – I've just made the corresponding angles of each exterior angle at the first one so that it forms a circle. Angle sum in a circle as we all know it is $360^{\circ}$ .

Tapas Mazumdar - 4 years, 4 months ago

@Tapas Mazumdar – yes, you have exactly said it.... (my/your idea)

Guillermo Templado - 4 years, 4 months ago

@Guillermo Templado – Very well. Thank you sir!

Tapas Mazumdar - 4 years, 4 months ago

@Tapas Mazumdar – Dont' call me sir, please. Call me Guillermo, you are my friend... Do you want me to write a proof about the sum of exterior angles of a $\text{ n - gon}$ is 360º? With words, of course....

Guillermo Templado - 4 years, 4 months ago

@Guillermo Templado – Yes, sure. I would love to see your proof!

Tapas Mazumdar - 4 years, 4 months ago

@Tapas Mazumdar – Ok, give me 30 minutes, more or less, please...

Guillermo Templado - 4 years, 4 months ago

@Guillermo Templado – Let $A$ be a $\text{n - gon}$ and $x_i, \space i = 1, 2, ..., n$ be its interior angles. Then, we know $\displaystyle \sum_{i = 1}^n x_i = (n - 2)\times 180º$ and sum of its exterior angles is $\displaystyle \sum_{i = 1}^n (180º - x_i)$ This implies, that $\text{sum of interior angles of A} + \text{ sum of exterior angles of A} =$ $= \displaystyle \sum_{i = 1}^n x_i + \sum_{i = 1}^n (180º - x_i) = n \times 180º \Rightarrow$ $\text{ sum of exterior angles of A} = \sum_{i = 1}^n (180º - x_i) = n \times 180º - (n - 2) \times 180º = 360º$

Guillermo Templado - 4 years, 4 months ago

@Guillermo Templado – Then, I have a question for you, Tapas (my friend). Are you able to make a picture explaining my idea? For example, could you explain my idea with a picture of a 10 -gon? This is not an obligation, it's a suggestion or a request... I repeat, this is not an obligation, if you want to make it, do it. If you don't want to make it, don't do it... I know, it'll take you much time. You can do it (if you want) in a week, for example... Anyway, you are not obligated to do it...

Guillermo Templado - 4 years, 4 months ago

@Guillermo Templado – Yes, sure why not!

Tapas Mazumdar - 4 years, 4 months ago

@Tapas Mazumdar – Thank you very much, be calm please, take a week at least, please... Be calm, please...

Guillermo Templado - 4 years, 4 months ago

@Guillermo Templado – I don't know. I pondered over your idea of explaining with only a picture proof itself but had to include words for the sake of understanding. This is my idea (sorry, for not taking a week):

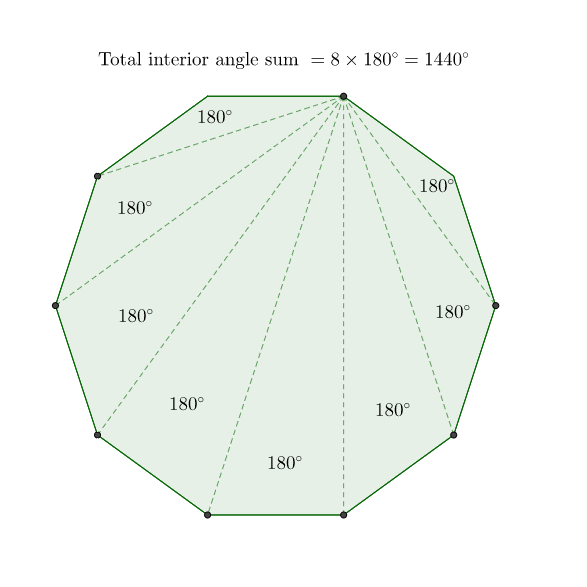
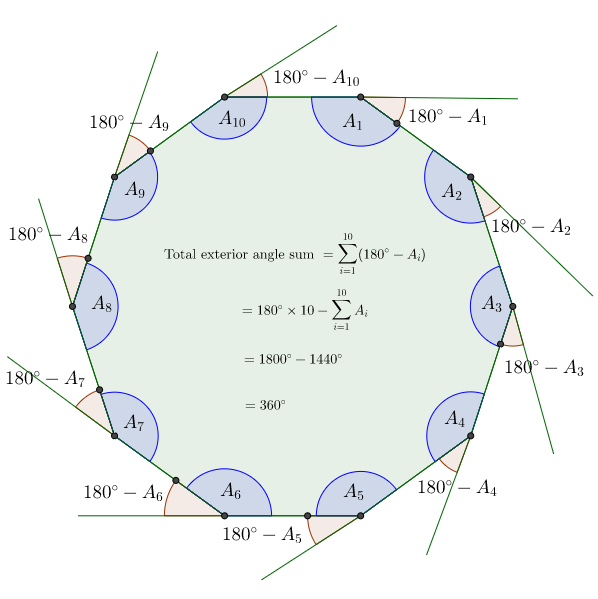Generalization can be done from the above result

Tapas Mazumdar - 4 years, 4 months ago

@Tapas Mazumdar – Excellent and wonderful (+1). Now, If I were you, I would paint one more pic, nevertheless, be calm please. Don't hurry up, please. I would paint the center of gravity ("centroid", I do not know exactly the name of this point in English) of the regular decagon, I mean the center of the circumradius of this regular decagon),and a small circle around the center of gravity(barycenter or centroid) of the regular decagon and I would paint the external angles,each one of them of one colour. How you can do it? Join the centroid of the regular decagon with the vertices of the regular decagon...(If you have somedoubt ask to me)... And then your picture would be in a frame of my room. It would be amazing ...

Guillermo Templado - 4 years, 4 months ago

@Guillermo Templado – 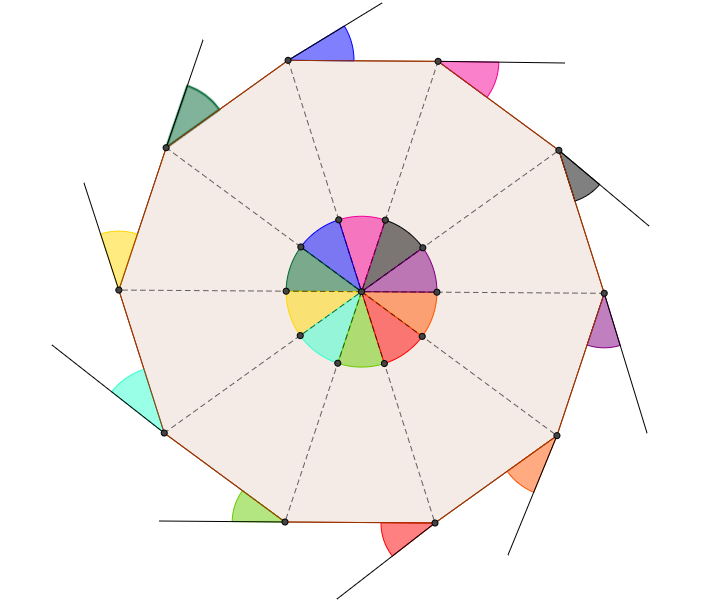I think your idea was wonderful. This is a really neat way to prove the exterior angle sum theorem. Here's your artwork as you wished for. Hope you like it!

Tapas Mazumdar - 4 years, 4 months ago

@Tapas Mazumdar – Exact (+ 1), magnific , now to the page...

Guillermo Templado - 4 years, 4 months ago

@Guillermo Templado – Thank you! I've added my works to this wiki. Thanks for motivating me to do so. :)

Tapas Mazumdar - 4 years, 4 months ago

@Tapas Mazumdar – And don't forget these pitures on this page . For me, these pictures explain much better the idea of sum of external angles of a n- gon is 360ª , and the sum of internal angles is $(n - 2)\times 180º$

Guillermo Templado - 4 years, 4 months ago

@Guillermo Templado – Thank you for adding them to this wiki. :)

Tapas Mazumdar - 4 years, 4 months ago

@Tapas Mazumdar – you are going to add it. YOU...

Guillermo Templado - 4 years, 4 months ago

@Guillermo Templado – Oh me! That's so humble of you.

Tapas Mazumdar - 4 years, 4 months ago

@Tapas Mazumdar – You are the artist and you have done it, so... come on...

Guillermo Templado - 4 years, 4 months ago

@Guillermo Templado – It would have been shorter if you would have skipped some steps like

Sum of interior angles is $\sum_{i=1}^n x_i = (n-2) \times 180^{\circ}$

And sum of exterior angles $\sum_{i=1}^n (180^{\circ} - x_i)$

Which can be further written as $\sum_{i=1}^n (180^{\circ}) - \sum_{i=1}^n x_i \\ \implies n \times 180^{\circ} - (n-2) \times 180^{\circ} \\ \implies 2 \times 180^{\circ} = 360^{\circ}$

But regardless, this was the exact proof which I was expecting! :)

Tapas Mazumdar - 4 years, 4 months ago

@Tapas Mazumdar – Yes, that's the one I was thinking of :)

You can make that into a "Proof without words"!

Chung Kevin - 4 years, 4 months ago

@Chung Kevin – It is indeed a proof without words. :)

Tapas Mazumdar - 4 years, 4 months ago

@Tapas Mazumdar – Very well done, please, continue posting on this page An advice: Look at the beggining and add a header. Example:

[[heading|Proof without words]]

Guillermo Templado - 4 years, 4 months ago

@Tapas Mazumdar – I have just written a header for this proof and I have just added this problem on this page

Guillermo Templado - 4 years, 4 months ago

Nashita Rahman
Jan 31, 2017

Let the angles of the smaller quadrilateral be a,b,c,d .

Sum of all the yellow angles ,

(180°- a ) + (180° - b ) + (180° - c) + ( 180 - d )

= 4.180° - ( a + b + c + d )

= 720° - 360° [since a+b+c+d = 360° as the sum of the angles of a quadrilateral is 360°]

=360°

Yay! Well said

Chung Kevin - 4 years, 4 months ago

Thank You:)

Nashita Rahman - 4 years, 4 months ago

@Nashita Rahman simple solution approach

Venkatachalam J - 4 years, 3 months ago

Mohammad Khaza
Jun 30, 2017

sum angle of any quadrilateral is 360.

so,there has been created four 180 degree angles. and (180x4)=720

so, summation of yellow angles are=720-360=360 degree

Achyuth Rao
Feb 2, 2017

One of the angle is right angle so some of other two is another 90° So 4×90=360

Yash Ghaghada
Mar 21, 2017

Forget about the inner quadrilateral for once Therefore the sum of the yellow angles and one extra angle with all yellow angle is(180 * 4 ) But that one extra is again a part of a quadrilateral Therefore the required sum is (180*4)-(360)=360

Roy Bertoldo
Feb 24, 2017

Sum of Yellow angles + sum of angles of the inscribed quadrilateral = 4 * 180 = 720

Sum of the angles of inscribed quadrilateral = 360

Sum of Yellow angles = 720 - 360 = 360

8 Yellow Angles

6 solutions

0 pending reports