849 second challenge
x 2 + y 2 = 8 4 9 − x 2 y 2
Find all possible x values to the equation above such that x and y are both positive integers. And state the values of x in ascending order with no spaces in between (e.g. if the solutions were 2 , 5 5 and 1 3 you would write " 2 1 3 5 5 ").
The answer is 24713.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Nice question and solution. One suggestion, though; I think you will need to add that y must be an integer as well, for as presently stated we can find a real number y for any given positive integer x that will satisfy the equation. :)
Log in to reply
If y is allowed to be a positive real number the number of solutions rises and x cqn be one of: 1 , 2 , 3 , 4 , 7 , 1 3
So @Sophie add in the condition that y is a positive real number as well.
Log in to reply
That was my first attempt, but then I realized that for any positive integer x we can find a positive real value y that satisfies the equation. To obtain Sophie's posted solution, it will need to be specified that y must be an integer.
Log in to reply
@Brian Charlesworth – Thank you both - I have edited it and hope this clears up any ambiguity. I forgot to specify that y must also be an integer!
@Brian Charlesworth – Actually I wasted two tries because too! Thankyou for clearing the ambiguity
Log in to reply
@Sualeh Asif – Sorry! I guess it's all very well thinking of a problem but you have to write down properly :) pleas let me know if there are any ambiguities
i just wrote an algorithm.. i hope its easy..
include <stdio.h>
include <math.h>
int main() { float n,m,i,j; int flag; for(i=0;i<30;i++){ flag=0; n = (849-(i i))/(1+(i i)); m=sqrt(n); j = (int)m; if(m>0 && j==m) flag=1; if(flag==1) printf("%d\n",(int)i ); } return 0; }
Thanks for writing this up.
x 2 + y 2 = 8 4 9 − x 2 y 2
⇒ x 2 + y 2 + x 2 y 2 = 8 4 9 x 2 y 2 + x 2 + y 2 + 1 = 8 5 0 ( x 2 + 1 ) ( y 2 + 1 ) = 8 5 0
We can use a spreadsheet to do the computation. Mine is as follows:
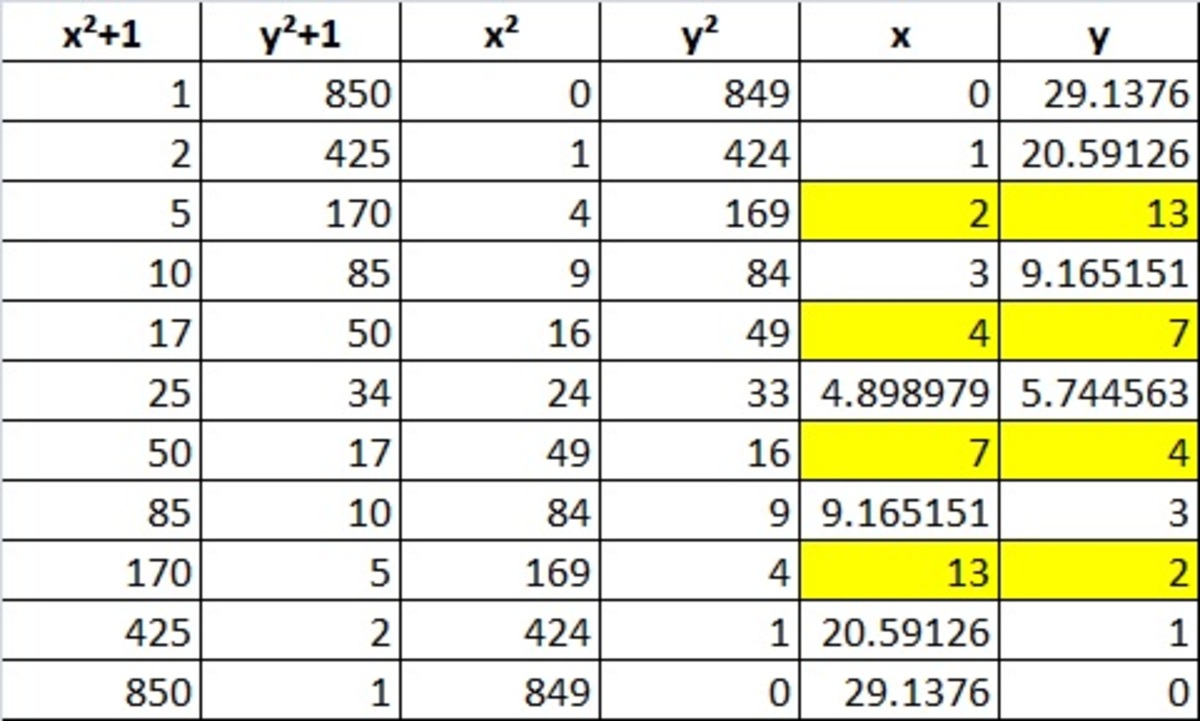
We note that x = { 2 , 4 , 7 , 1 3 } . Therefore, the required answer is 2 4 7 1 3
In the first quadrant, the maximum values of x and y are both less than 30.
It's a simple matter to check the space of integer values of x and y for those that adhere to this relation.
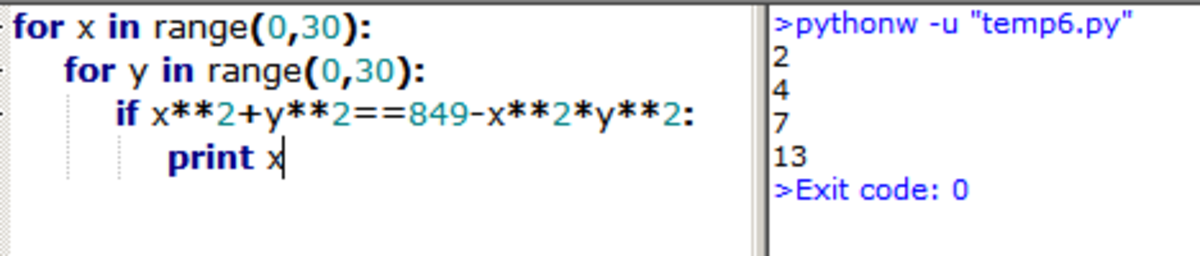
How did the author of the problem do it?
PS: Incidentally, this way of providing for solutions of problems opens up a lot of possibilities!
I really like this method - not being able to code very well myself I am always impressed with answers like this. I have now also posted my own solution if you'd like to see an entirely different way of doing it.
Log in to reply
I've been writing code for some many years that I have difficulty thinking in any other way.
Seeing as someone asked, this is my solution.
x 2 + y 2 = 8 4 9 − x 2 y 2
x 2 y 2 + x 2 + y 2 = 8 4 9
x 2 y 2 + x 2 + y 2 + 1 = 8 5 0
( x 2 + 1 ) ( y 2 + 1 ) = 8 5 0
The pairs of factors of 850 can now be considered.
8 5 0 = 1 × 8 5 0
8 5 0 = 2 × 4 2 5
8 5 0 = 5 × 1 7 0
8 5 0 = 1 0 × 8 5
8 5 0 = 1 7 × 5 0
8 5 0 = 2 5 × 3 4
It is clear that there are two occasions when both in the pair are one more than a square number so the possible solutions are:
x 2 + 1 = 5 and y 2 + 1 = 1 7 0 (and vice versa)
or x 2 + 1 = 1 7 and y 2 + 1 = 5 0 (and vice versa)
Therefore x = 2 or 1 3 or 4 or 7 .
Of course, I had the advantage that I wrote the question for a friend with certain techniques in mind, though it is great to see other methods that I hadn't considered!