Too much of calculation?
Find the value of 2 4 7 9 8 2 − 2 4 7 9 6 2 .
Note: Please don't use a calculator.
The answer is 99188.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
55 solutions
Moderator note:
Yes, this is just the difference of two perfect squares identity. Bonus question: Find the best approach to evaluate 2 4 7 9 8 3 − 2 4 7 9 6 3 without using a calculator.
Creative thinking. Honestly, I didn't think of this!
T h u m b s u p ! ! !
@Nihar Mahajan , it would be great if we extend our relationship by being friends! What do you have to say?
Log in to reply
Log in to reply
I meant closer friends. . . Anyways thanks for accepting my request!
Hi, I just got confused on the second line. I know the difference of squares means it can be factored but why is the expression in the second parentheses (a + 1 - a + 1)? If a^2 - b^2 = (a+b) (a-b), and by substitution of the values, shouldn't it read (a+1 + a-1)(a+1-a-1)?
Log in to reply
Its a + 1 − ( a − 1 ) = a + 1 − a + 1 = 2 .You must put the brackets before you perform subtraction.
bro cant we take square as whole then it would be (24798-24796)^2 then the square of 2 =4
Log in to reply
a 2 − b 2 is not equals to ( a − b ) 2 .
That's how I thought it should be solved.
Why make 2 polynomials when you can just do one. Try quantity -2 squared and you save half your effort!
In response to the Challenge Master note:
Using the Difference of Cubes formula:
a 3 - b 3 =(a-b)( a 2 +ab+ b 2 )
You can simplify the latter half of the above equation into
(a-b)( a 2 +ab+ b 2 )=(a-b)[ ( a + b ) 2 -ab]
Let a= 24798 and b =24796
2 4 7 9 8 3 - 2 4 7 9 6 3 =(24798-24976)[( 2 4 7 9 8 + 2 4 7 9 6 ) 2 -24798*24796]
=(2)[ ( 4 9 5 9 4 2 -24798*24796]
=(2)*[2459564836-614891208]
=(2)*(1844673628)
=3689347256
As you can see, this is a very calculation-intensive way to solve but it is one of the faster ways to solve it in my opinion, assuming you don't mess up the large multiplications. It is, however, a better way than cubing both 24798 and 24796 and taking the absolute value of their difference.
Log in to reply
There's an easier approach.
Note that a = b + 2 . I would have tried letting c = 2 4 7 9 7 , then the expression becomes ( a + 1 ) 3 − ( a − 1 ) 3 . Expand with binomial expansion. Can you finish it off from here?
Log in to reply
Yes , indeed this is the simplest approach.
( a + 1 ) 3 − ( a − 1 ) 3 = [ a + 1 − ( a − 1 ) ] [ ( a + 1 ) − ( a − 1 ) 2 + 3 ( a + 1 ) ( a − 1 ) ] = 2 [ 4 + 3 a 2 − 3 ] = 2 [ 1 + 3 a 2 ] = 2 [ 1 + 3 ( 2 4 7 4 7 ) 2 ] = 2 [ 1 8 3 7 2 4 2 0 2 7 + 1 ] = 3 6 7 4 4 8 4 0 5 6
Log in to reply
@Nihar Mahajan – You can almost immediately jump to 2 ( 1 + 3 a 2 ) . Hint: Binomial expansion, ( A ± B ) 2 = … , instead of applying the difference of perfect cubes identity.
Now, what is the best way to calculate 2 4 7 4 7 2 (and still without using calculator)? Hints: 2 4 7 4 7 = 2 5 0 0 0 − 2 5 0 − 3 and expand ( a − b − c ) 2 .
We should not always be dependent on calculators all the time.
The expression is wrong in the first place. If you intend to square the numbers, the right expression should be (24798)^2 - (24796)^2 not 24798^2 -24796^2. You are confusing the readers. Let us say a = 2, b = 4, c = 7, d = 9, can you say abcdc+1^2 the same as abcd(c+1)^2 the same? or abcdc-1^2 the same as abcd(c-1)^2?
i HAVE A DIFFERENT APPROACH: let x=24798. Then the problem reads x^2-(x-2)^2. This transalates into 2x+ 4. Hence 2*24798+4 that transforms into 49600.
Log in to reply
x^2 - (x-2)^2 = x^2 - (x^2 - 4x + 4) = 4x - 4. and 4 (24,798) - 4 = 99,188
it translates to 4x+4 not 2x+4
We can also use this formula but it's a bit lengthier than Nihar Mahajan's,
Let, a = 2 4 7 9 8 and b = 2 4 7 9 6
Use, a 2 − b 2 = ( a + b ) ( a − b )
Substituting the values we get,
2 4 7 9 8 2 − 2 4 7 9 6 2 = ( 2 4 7 9 8 + 2 4 7 9 6 ) × ( 2 4 7 9 8 − 2 4 7 9 6 ) = ( 4 9 5 9 4 ) × ( 2 ) = 9 9 1 8 8
this problem could be solved easily by using the formula that i created i.e.
( a + 2 ) 2 - ( a ) 2 = 4 × ( a + 1 )
Be careful with notation. Before starting, you should have defined 'a' . In that case, a = 24796. But if had used this formula: [ a^2 - (a-2)^2) = 4 x (a-1) ], then the value of 'a' had been a=24796. This can look like something trivial but in mathematics you can never give a solution with a non-defined expression.
Likewise, congratulations for your result. That's right. Go on practising !!
Mine was this approach. :)
Be x = 24798.
Then one can write
x 2 − ( x − 2 ) 2
= x 2 − ( x 2 − 4 x + 4 )
= x 2 − x 2 + 4 x − 4
= 4 x − 4
= 9 9 1 8 8 .
The given problem is to find the difference of two alternate squared number.
We can see that :
2^2 - 0^2 = 4
3^2 - 1^2 = 8
4^2 - 2^2 = 12 and so on.
We can see this as an Arithematic Progression with first term a = 4 and common difference d = 4.
24798^2 - 24796^2 is the 24797th term of this AP.
n = 24797
a n = a o + (n-1)d
Solution is : 4 + (24797-1)4 = 99188
n^2-(n-2)^2=4(n-2)+4Write a solution.
That +4 could factor in to make it 4(n-1)
a^2 - b^2 = (a+b)(a-b)= 49594×2= 99188
You can also solve using (A square) minus (B Square) formula: (A-B) (A+B) 24798+24796=49594 (A+B) 24798-24796=2 (A-B) 49594 2=99188
One can also use a = 24796 and b = 2 then
(a+ b) 2 - a 2
= 2ab + b 2
=( 2a)(2) + 4
= 4a + 4 = 99184 +4 = 99188
Write a solution. (24796+2)^2 -(24796)^2 = 4 + 2x24796x2 = 4 (1+24797) = 99188
it can be solved using the formula square distrubutive
The same class 8th property... a 2 − b 2 = ( a + b ) ( a − b )
So, 2 4 7 9 8 2 − 2 4 7 9 6 2 = ( 2 4 7 9 8 + 2 4 7 9 6 ) ( 2 4 7 9 8 − 2 4 7 9 6 ) = 4 9 5 9 4 × 2 = 9 9 1 8 8
we will use the property of (a+b)(a-b)
since it's equal that (24796+2)^2-24796^2,then let x=24796 =(x+2)^2-x^2 =x^2+4x+4-x^2 =4x+4 =4(24796)+4 =99,188
Apply formula (a+1)^2 --(a-1)^2= 4a, where a=24797
It's a pattern, at first I too was stumped, but it clicked after a minute. I'm just glad to have learned something new today, I never knew such a pattern existed. The answer is the sum total multiplied by the difference. Like so:
3 squared = 3 * 3 = 9, and 2 squared = 4.
The results, 9 - 4 = 5
While 3 + 2 = 5
4 squared is 16, and 3 squared is 9.
16 - 9 = 7
4 + 3 = 7
4 - 3 = 1
1 * 7 = 7
The difference between the two is the same as the sum in those cases. Continuing:
6 squared is 36, 4 squared is 16.
36 - 16 = 20
6 + 4 = 10
6 - 4 = 2
2 * 10 = 20
So the answer of what squared subtract whatever else squared, is the same as the numbers added and multiplied by the difference between them. So if the numbers are 2 apart, then multiply by 2, if 3 apart, multiply by 3, etc.
So 24798^2 -24796^2 is the same as:
(24798 + 24796) * (24798 - 24796) =
(49594) * (2) =
99188
Pardon the informality, it's just a much easier explanation than those that require a stronger background in mathematics. The underlying logic is more important if someone is looking for the answer.
24798^2 - 24796^2 = (24798 - 24796)(24798 + 24796) = 2 x 49594 = 99188
Not sure if the best or shortest but it is different from other responses
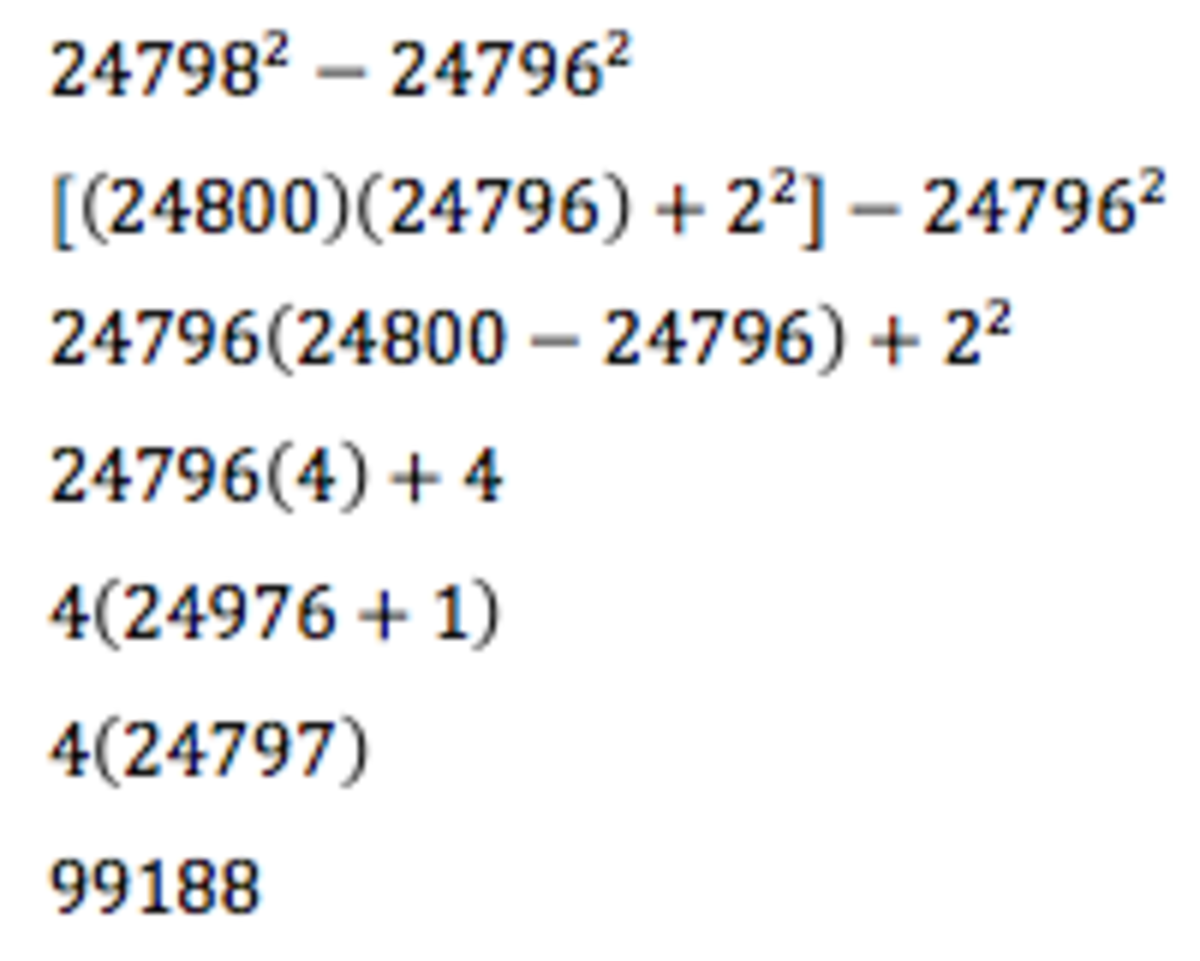 .
.
The difference between 24796 and 24798 is two. If n becomes the value 24796 then you can therefore write the expression: (n+2)² - n², which equates to: n² + 4n + 4 - n², which can simplify to: 4n + 4. Replacing n with 24796 will give the number 99188
Using formula: a^2-b^2=(a+b)(a-b)
Mine is pretty weird since I try to solve it using number pattern.
4 2 − 2 2 = 12 = ( 4 × 2 ) + ( 2 × 2 )
1 2 2 − 1 0 2 = 44 = ( 1 2 × 2 ) + ( 1 0 × 2 )
SO,
2 4 7 9 8 2 − 2 4 7 9 6 2 = 99188= ( 2 4 7 9 8 × 2 ) + ( 2 4 7 9 6 × 2 )
I haven't try to figure it out, but I believe it's only true if it differs by 2..
24798^2 - 24796^2
let x = 24796
= (x+2)^2 - x^2
= x^2 + 4x + 4 - x^2
= 4x + 4
substituting back x with 24796
= (4 * 24796) + 4
= 99184 + 4
= 99188
a^2-b^2 i.e (a-b)×(a+b) so 2×49595 = 99188
Simple solution, for example take (3)^2-(1)^2 = 8 (4)^2-(2)^2= 12 (5)^2-(3)^2= 16 therefore we get, (n)^2 - (n-2)^2 = 4(n-1) So, (24798)^2 - (24796)^2 = 4(24797) = 99188
(a+1) x (a+1) - a x a = 2a+1 = a + (a+1)
just do it twice an you got (24796+24797 ) + (24797+24798)
its easy! (24798-24796) (24798+ 24798-2) =2(24798 2 -2) = 24798x4 - 4 =99188
let smaller number be n . So , given expression is, (n+2)^2 - n^2 = (n^2 + 4 n + 4 -n^2) = (4 n + 4) = 4*(n+1)
Even for multiplication of a large number, i.e. 24797 we might use a calculator, bt for addition we can avoid calculator. we can also use: a^2 - (a-1)^2 = a+a-1 so, 24798^2 - 24796^2 = 24798^2 - 24797^2 + 24797^2 - 24796^2 = 22798+ 2*24797+24796 = 99188
(24798)^2 - 24796 can be written as (24796+2)^2 - 24796 that equals =4+4(24796) =4+99184 =99188
let h=24798
h^2 - (h-2)^2
=h^2 - (h^2 -4h +4)
=4h-4
substitute the value of h =4(24798) -4 =99192 -4 =99188
Lets feel something interesting :D
if we observe this 4^2-2^2=12,6^2-4^2=20,8^2-6^2=28,then we can establish an equation.let's assume that,b=a-2.so,a^2-b^2=(a+b)x2. here,24798^2-24796^2=(24798+24796)x2=99188
(a + b) * (a - b) 49594 * 2 = 99188
Simply find a pattern, start out with smaller numbers such as 4^2- 3^2=7; 4+3=7 Try another 5^2-4^2=9; 5+4=9 See a pattern, the bases added together equal the answer. Now separate the bases by 2, 7^2-5^2= 24, which is the bases added together times 2, try with another, it works. So apply that pattern to this problem, 24798^2-24796^2= (24798+24796)*2 which equals 99188!
I like your pattern approach -- well done :)
Let a=24797
{(a+1)^2} - {(a-1)^2}
{(a+1)(a+1)} - {(a-1)(a-1)}
{(a^2)+2a+1} - {(a^2)-2a+1}
{(a^2)-(a^2)+2a+2a+1-1}
2a+2a
4a
(4)(24797) = 99188
Everyone is doing the equation but I'm over here doing the whole process of 24798 24798 - 24796 24796 and ultimately getting 99188. Lol
((a-b)^2)x((a-c)^2) =((24800-2)^2 ) x((24800-4)^2) =4(24800) -12 =99188
Same idea, but in reference to the smaller number: Add 1 to the smaller number and multiply by 4.
(a+2)^2 - a^2 = 4×(a+1)
E.g. 2^2 - 0^2 = 4×(0+1) = 4
Or. 3^2 - 1^2 = 4×(1+1) = 8
(24798+24796)x(24798-24796)=49594x2=99188 Let 24798=a , 24796=b. So a^2xb^2 =(a+b)x(a-b)=49594x2=99188
24798 = 24796 + 2
(24796 + 2)^ 2 = 24796^2 + 2^2+2.2.24796
24796^2 will get eliminated.
Left terms are 2^2 +2.2.24796 = 4+99184 =99188
a^2 -b^2 =(a+b)(a-b) So 24798^2 - 24796^2 =(24798+24796) (24798 -24796) =49594 2=99188
Let a= 24796^2 and b= 2 therefore (a +b ) ^2 - (a ^2) is answer that is 2 a b+ b^= 2* 24796 *2 + 2^2
24798^2-24796^2=(24796+2)^2+24796^2=(24796^2+2 2 24796+2^2)-24796^2=4*24796+2^2=99184+4=99188
(a + b) * (a - b)
49594 * 2
= 99188
(24798 X 24798 ) - (24796 X 24796) equals 99188
24798^2-24796^2=(24796+2)^2-24796^2 =24796^2+2^2+2 24796 2-24796^2 =2^2+2 24796 2 =99188
(a+b) * (a-b) = (24798+24796) * 2 = 99188
Let's make things simple. 4 - 1 = 1 + 2. 9 - 4 = 2 + 3. By that logic, 24798^2 - 24796^2 = (24798 + 24797) + (24797 + 24796)
a^2-b^2= (a-b) (a+b)=> 2 (24798+24796)=99188

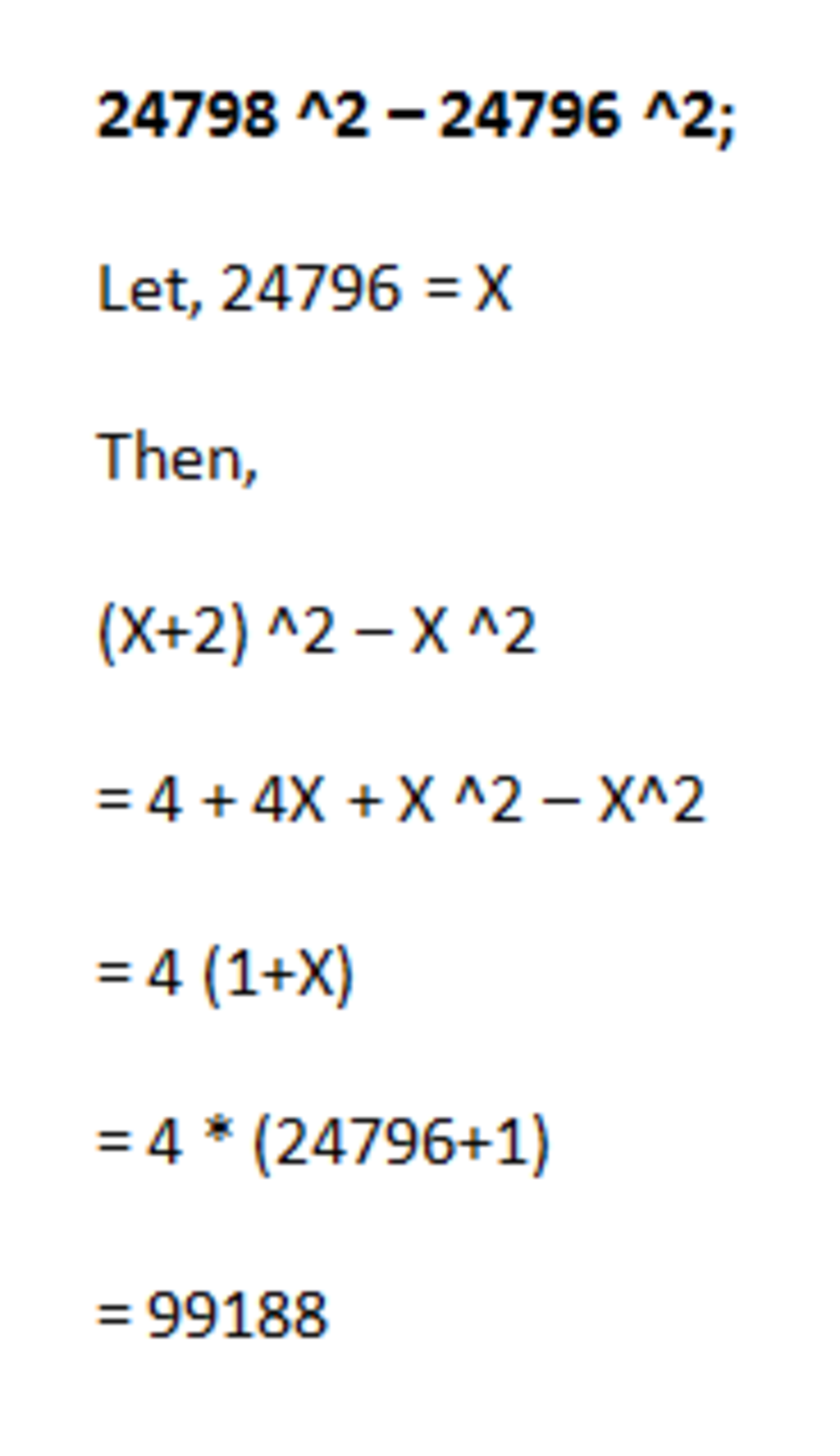
Let 2 4 7 9 7 = a .Thus the expression becomes :
( a + 1 ) 2 − ( a − 1 ) 2 = ( a + 1 + a − 1 ) ( a + 1 − a + 1 ) = 2 a ( 2 ) = 4 a = 9 9 1 8 8