Remember it's cyclic
A N B M is a cyclic quadrilateral such that A N = a , B N = b , and ∠ M N A = ∠ M N B = 6 0 ∘ .
What is the length of diagonal M N ?
Bonus : Use geometry
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
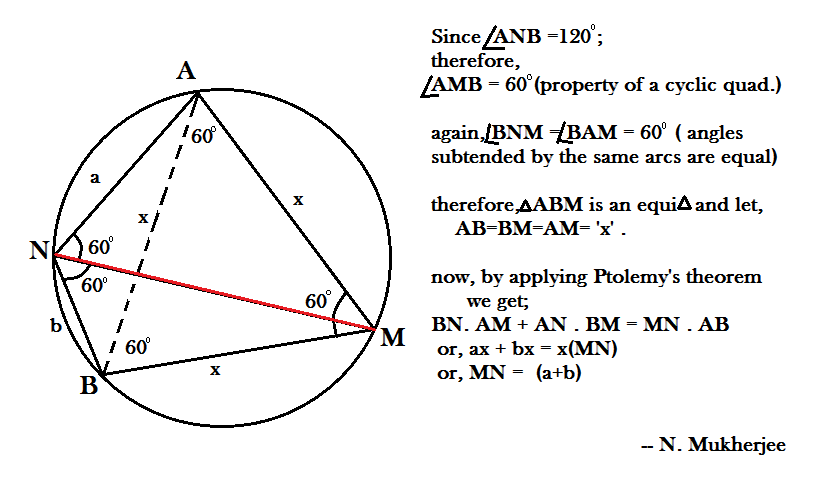
Nice to use ptolemy!
Log in to reply
thanks! .n..tbh... admirable profile name ..
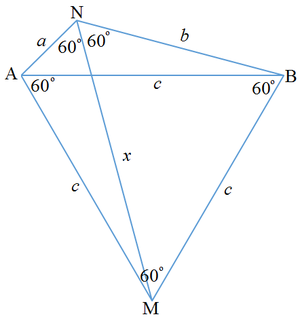
Since A N B M is a cyclic quadrilateral , the opposite angles ∠ A N B + ∠ A M B = 1 8 0 ∘ ⟹ ∠ A M B = 6 0 ∘ . Also ∠ M B A = M N A = 6 0 ∘ and ∠ M A B = ∠ M N B = 6 0 ∘ . Therefore △ A B M is equilateral and A B = B M = M A = c .
Let the length of diagonal M N be x . Then applying Ptolemy's theorem : the product of the lengths of the two diagonals of a cyclic quadrilateral is equal to the sum of the products of opposite sides, we have x c = a c + b c ⟹ M N = x = a + b .
what a coincidence sir!.... in time and approach... :P
Nice approach sir
Glad that you like the solution. Upvote?
Log in to reply
sure! sir upvoted... what abt mine? :P
Done sir :D
Sir, can you guide me to some maths books with challenging problems and good explanations??
Log in to reply
I am sorry, I hardly read any book nowadays. I don't know any good books for math.
Log in to reply
@Chew-Seong Cheong – Ok sir, no problem, can you tell how you created the figure in solution?
Log in to reply
@Mr. India – I used Microsoft Excel spreadsheet to graph out the figure. Removed all the axes and grids then copied it to Paint to complete the figure.
Log in to reply
@Chew-Seong Cheong – Oh hard work! B-) thnx btw
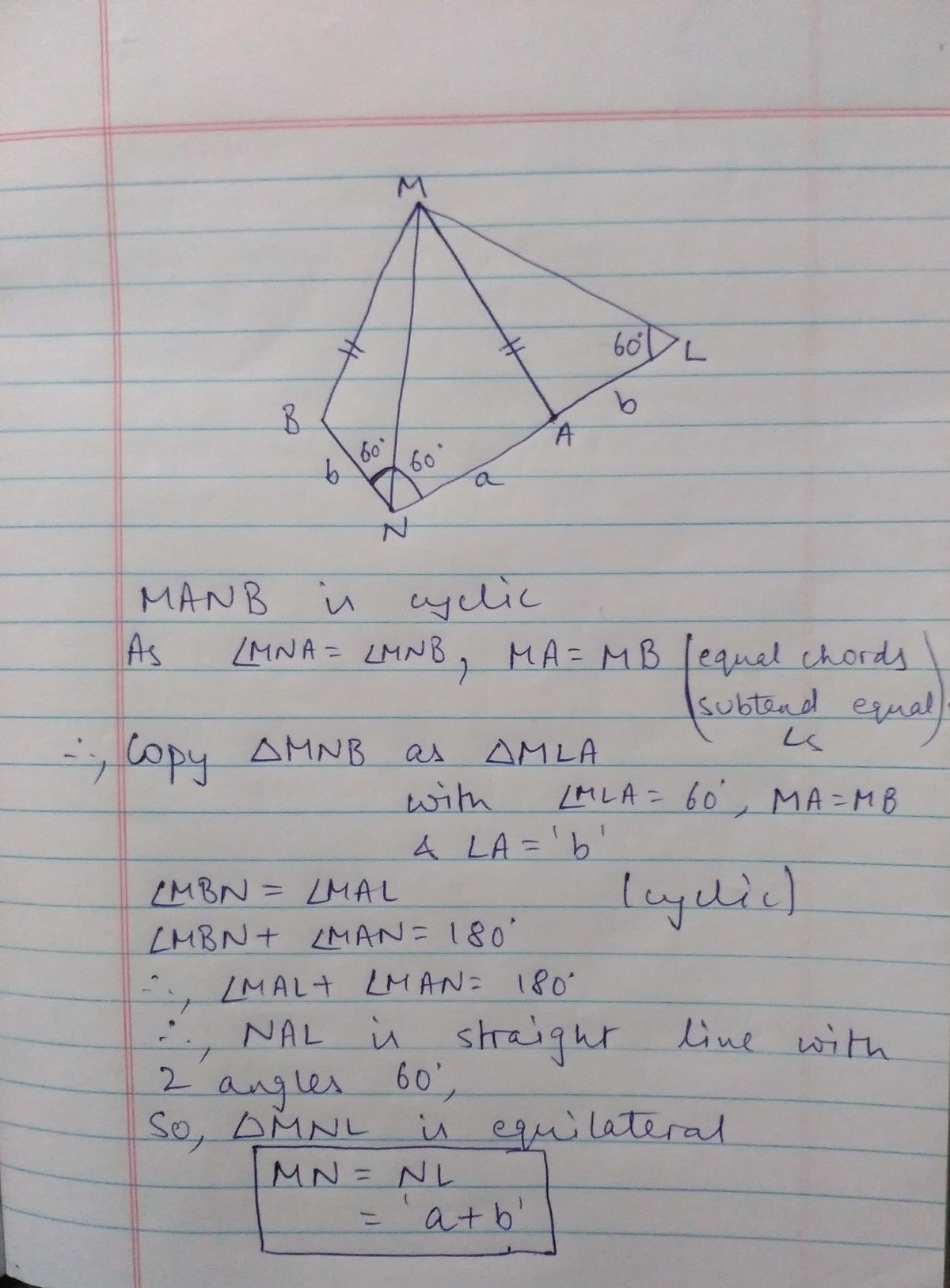
Please ask if you don't understand something