A Ball in a Cone? Is that something new?
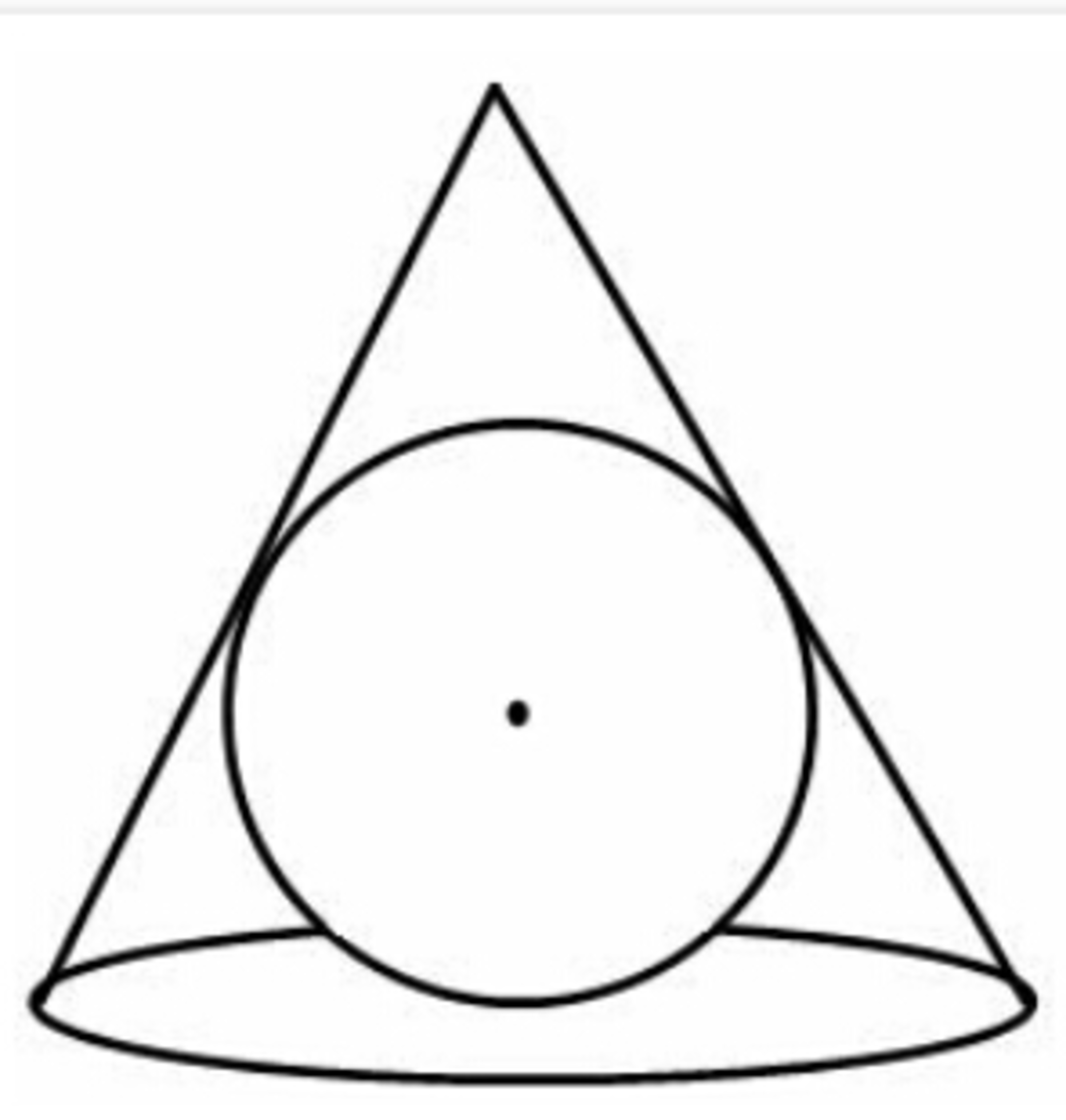
There's a ball in a cone. Let the radius of the ball is r cm and the radius of cone is R cm.
The height of the cone is h cm and the lateral height (the length of a line segment from the apex of the cone along its side to its base) is l cm.
If
R + h = 1 1 2
h + l = 1 4 4
l + R = 1 2 8
What is the ratio between the volume of ball and the volume of cone?
The answer is the form of x : y . Submit your answer as ( x 2 + 3 x y + y 2 ) ( x 2 + x y + y 2 ) .
Try another problem on my set! Let's Practice
The answer is 14065.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Tapas Mazumdar Nice solution. I thought your solution is much better than mine...
Log in to reply
Thanks. But you solution has a nice and a different approach, and it is nice too. :)
Log in to reply
Thanks.. Stay tuned.. Hehehehe
I am thinking ahout the level.. How about you??
Log in to reply
@Fidel Simanjuntak – I would say a Level 3 or 4.
Log in to reply
@Tapas Mazumdar – Really? Okay, I'll confirm it.. Thanks for your suggestion
R + h = 1 1 2 . . . . . . . . . . ( 1 )
h + l = 1 4 4 . . . . . . . . . . ( 2 )
l + R = 1 2 8 . . . . . . . . . . ( 3 )
( 1 ) + ( 2 ) + ( 3 )
2 ( R + h + l ) = 3 8 4
R + h + l = 1 9 2 . . . . . . . . . . ( 4 )
( 4 ) − ( 2 )
R = 4 8 ; By Triple Pythagoras, h = 6 4 ; l = 8 0
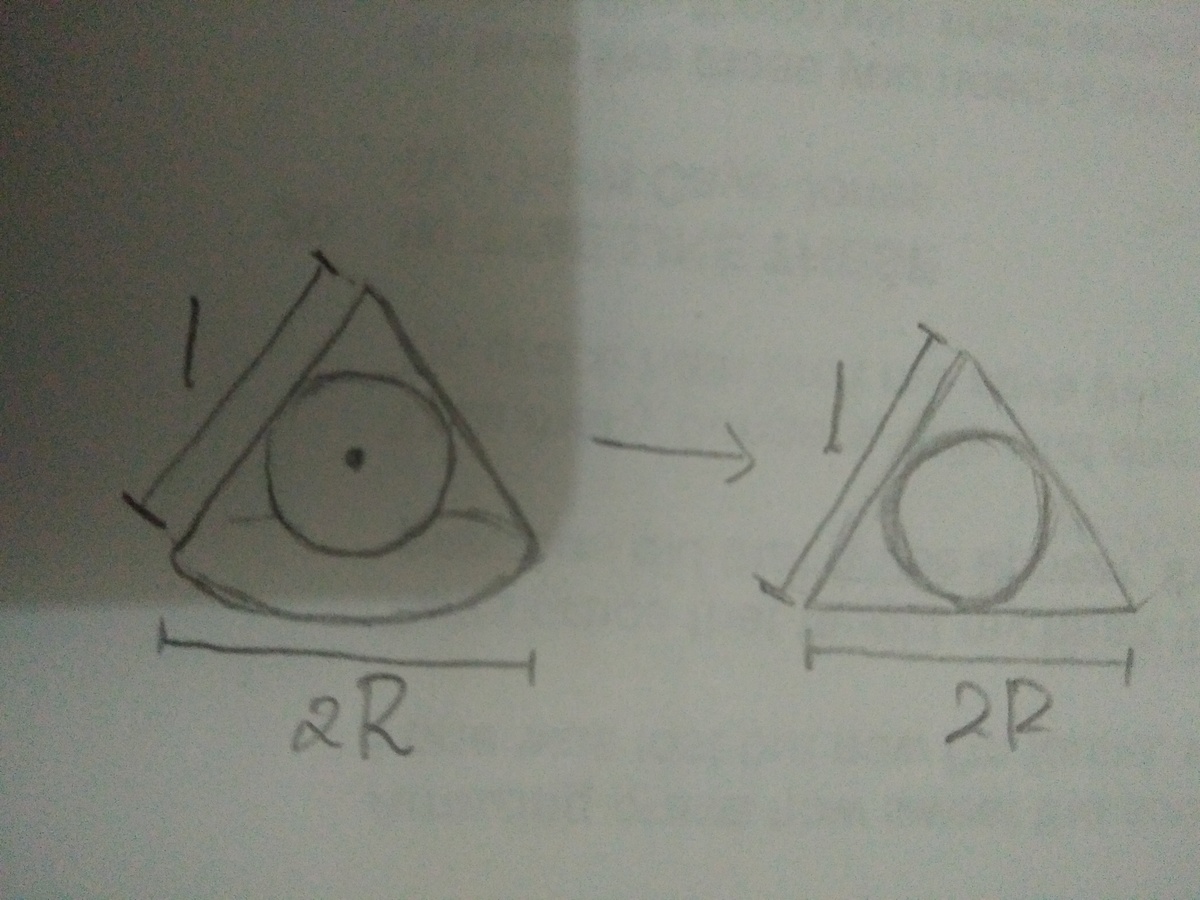
r = 2 1 × ( 2 R + 2 l ) 2 R h × 2 1
r = 2 ( R + l ) 2 R h
r = R + l R h
r = 1 2 8 3 0 7 2
r = 2 4
Volume of Ball : Volume of Cone
3 4 × π × r ³ : 3 1 × π × R ² × h
4 × 2 4 × 2 4 × 2 4 : 4 8 × 4 8 × 6 4
3 : 8 = x : y
x = 3 ; y = 8
Note that x ² + 3 x y + y ² = x ² + 2 x y + y ² + x y = ( x + y ) ² + x y and
x ² + x y + y ² = x ² + 2 x y + y ² − x y = ( x + y ) ² − x y
Now,
( ( x + y ) ² + x y ) ( ( x + y ) ² − x y ) = ( x + y ) 4 − ( ( x y ) 2 )
1 1 4 − 2 4 2 = 1 4 6 4 1 − 5 7 6
= 1 4 0 6 5
@Tapas Mazumdar - Can you give a solution?
R + h h + l l + R = = = 1 1 2 ⋯ ( 1 ) 1 4 4 ⋯ ( 2 ) 1 2 8 ⋯ ( 3 )
( 1 ) + ( 2 ) + ( 3 ) gives,
2 ( l + R + h ) = 3 8 4 ⟹ ( l + R + h ) = 1 9 2 ⋯ ( 4 )
( 4 ) − ( 1 ) gives,
l = 8 0
( 4 ) − ( 2 ) gives,
R = 4 8
( 4 ) − ( 3 ) gives,
h = 6 4
Consider the diagram above of half-conical section where θ is exactly half of the original angle made at the apex.
Using trigonometry, we have,
cos θ = l h = 8 0 6 4 = 5 4 ∴ sin θ = 1 − cos 2 θ = 5 3
From the figure, we observe that,
sin θ = h − r r ∴ h − r r = 5 3 ⟹ 6 4 − r r = 5 3 ⟹ r = 2 4
Thus,
Volume of cone Volume of ball = = = = = 3 1 π R 2 h 3 4 π r 3 4 8 2 ⋅ 6 4 1 6 4 1 ⋅ 2 4 3 2 4 2 1 ⋅ 2 2 ⋅ 1 6 2 4 3 2 4 6 4 2 4 8 3 = y x
Hence,
( x 2 + 3 x y + y 2 ) ( x 2 + x y + y 2 ) = [ ( x + y ) 2 + x y ] [ ( x + y ) 2 − x y ] = ( x + y ) 4 − ( x y ) 2 = ( 3 + 8 ) 4 − ( 3 × 8 ) 2 = 1 1 4 − 2 4 2 = 1 4 6 4 1 − 5 7 6 = 1 4 0 6 5