An odd integral
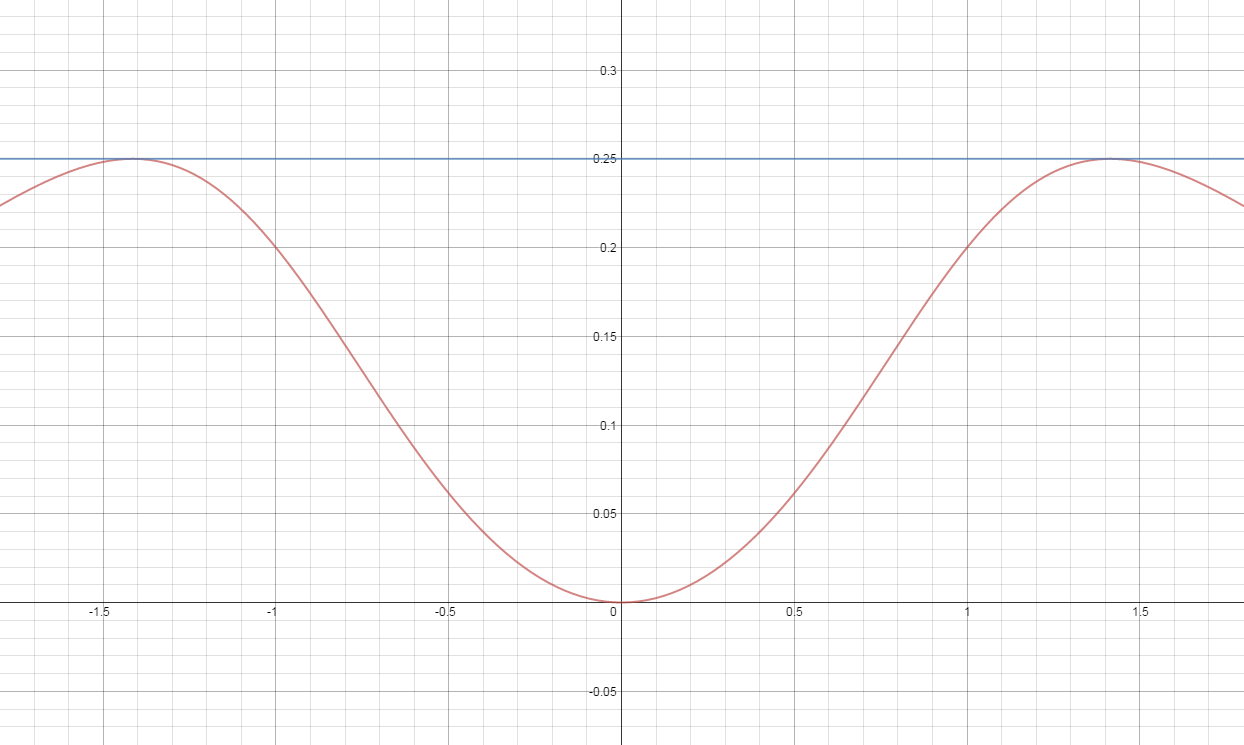
The image above shows the graph for f ( x ) = x 4 + 4 x 2 . By drawing a tangent line at either absolute maximum for f ( x ) , one can bound a finite region above f ( x ) that ends at the y -value for these maxima.
What is the area of this region?
This problem is original. The picture of the graph was produced from Desmos .
The answer is 0.362395411.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
One of the most impressive solutions which I have seen in a long time. I was waiting for this! :D +1
nice one!!!!+1!!!!
Can't 4 1 tanh − 1 ( 3 2 2 ) also be written as 2 1 tanh − 1 ( 2 2 ) ?
Log in to reply
It can be. I believe 11 is another acceptable solution to the problem.
Log in to reply
If you have a comment like this, post a report, and don't just comment on a solution. It has taken a month for my report to be handled, which raised the same issue. If multiple reports had been posted, the problem would have been resolved sooner!
Log in to reply
@Mark Hennings – I apologize; I have not been active at all on Brilliant.org for the past year or so. College takes you away for sure! I hope to be more active again sometime in the future.
I see that someone has edited the problem, so now it's a numerical answer, rather than the symbolically-based form which I originally put there. I apologize for being careless and not checking if my answer was unique previously. I hope that your points were restored, if that's what you're worried about.
Section I. Finding Global Maxima
Finding global maxima of f ( x ) , f ′ ( x ) 0 ⟹ x = ( x 4 + 4 ) 2 ( x 4 + 4 ) ⋅ 2 x − x 2 ⋅ 4 x 3 = ( x 4 + 4 ) 2 − 2 x 5 + 8 x = − 2 x ( x 4 − 4 ) = ± 2 which show that the global maxima are ( 2 , 4 1 ) and ( − 2 , 4 1 ) .
Section II. Integration
Note: Instead of doubling the halved region, the best way to obtain the close form is to compute the integral the long way. Doubling the halved region gives the same results, but different values. You need to then match the corresponding terms with your answer to find the matching values.
Call t ( x ) = 4 1 the equation of the line tangent to two points of f ( x ) . Since t ( x ) ≥ f ( x ) at − 2 ≤ x ≤ 2 , the area integral is ∫ − 2 2 ( 4 1 − x 4 + 4 x 2 ) d x which is also ∫ − 2 2 4 1 d x − ∫ − 2 2 x 4 + 4 x 2 d x Clearly, ∫ − 2 2 4 1 d x = 2 2 = 2 1 which yields 2 1 − ∫ − 2 2 x 4 + 4 x 2 d x For the remaining integral, since x 4 + 4 = ( x 2 + 2 x + 2 ) ( x 2 − 2 x + 2 ) by partial decomposition, we have − ∫ − 2 2 ( 4 ( x 2 − 2 x + 2 ) x − 4 ( x 2 + 2 x + 2 ) x ) d x = 4 1 ∫ − 2 2 ( x 2 + 2 x + 2 x − x 2 − 2 x + 2 x ) d x For each decomposed fraction, express x = x + ( 1 − 1 ) and x 2 + 2 x + 2 = ( x 2 + 2 x + 1 ) + 1 = ( x + 1 ) 2 + 1 x 2 − 2 x + 2 = ( x 2 − 2 x + 1 ) + 1 = ( x − 1 ) 2 + 1 so 4 1 ∫ − 2 2 ( x 2 + 2 x + 2 x + 1 − ( x + 1 ) 2 + 1 1 − ( x 2 − 2 x + 2 x − 1 + ( x − 1 ) 2 + 1 1 ) ) d x = 4 1 ∫ − 2 2 ( x 2 + 2 x + 2 x + 1 − x 2 − 2 x + 2 x − 1 − ( ( x + 1 ) 2 + 1 1 + ( x − 1 ) 2 + 1 1 ) ) d x Integrating by substitution, 4 1 ( 2 1 ( ln ( x 2 + 2 x + 2 ) − ln ( x 2 − 2 x + 2 ) ) − ( arctan ( x + 1 ) + arctan ( x − 1 ) ) ) ∣ ∣ ∣ ∣ x = − 2 x = 2 which by arctan ( p ) + arctan ( q ) = arctan ( 1 − p q p + q ) gives ⟹ 4 1 ( 2 1 ln ( x 2 − 2 x + 2 x 2 + 2 x + 2 ) − arctan ( 2 − x 2 2 x ) ) ∣ ∣ ∣ ∣ x = − 2 x = 2 4 1 ( 2 1 ln ( x 2 − 2 x + 2 x 2 + 2 x + 2 ) − arcsin ( x 4 + 4 2 x ) ) ∣ ∣ ∣ ∣ x = − 2 x = 2 So by Fundamental Theorem of Calculus, = = = 4 1 ⎝ ⎛ 2 1 ( ln ( 2 2 − 2 2 + 2 2 2 + 2 2 + 2 ) − ln ( 2 2 + 2 2 + 2 2 2 − 2 2 + 2 ) ) − ⎝ ⎛ arcsin ⎝ ⎛ 2 4 + 4 2 2 ⎠ ⎞ − arcsin ⎝ ⎛ − ( − 2 ) 4 + 4 2 2 ⎠ ⎞ ⎠ ⎞ ⎠ ⎞ 4 1 ( 2 1 ( ln ( 2 − 2 2 + 2 ) − ln ( 2 + 2 2 − 2 ) ) − ( arcsin ( 1 ) − arcsin ( − 1 ) ) ) 4 1 ( 2 1 ln ( ( 2 − 2 ) 2 ( 2 + 2 ) 2 ) − π ) 4 1 ( 2 1 ln ( 6 − 4 3 6 + 4 3 ) − π ) Since tanh − 1 ( z ) = 2 1 ln ( 1 − z 1 + z ) Inside ln , divide each term by 6 , so 2 1 ln ⎝ ⎜ ⎜ ⎜ ⎜ ⎛ 1 − ( 3 2 2 ) 1 + ( 3 2 2 ) ⎠ ⎟ ⎟ ⎟ ⎟ ⎞ = tanh − 1 ( 3 2 2 ) So, 4 1 ( tanh − 1 ( 3 2 2 ) − π ) = 4 1 tanh − 1 ( 3 2 2 ) − 4 π = 4 1 tanh − 1 ( 3 2 2 ) − arcsin ( 2 1 ) Thus, the area of the integral is 4 1 tanh − 1 ( 3 2 2 ) − arcsin ( 2 1 ) + 2 1 where a = 4 , d = 3 , b = c = e = f = 2 ⟹ a + b + c + d + e + f = 1 5