A Race To Negative Infinity

Make the substitution u = - x, then $\lim_{x \to -\infty} \sqrt{x^2 + 2x} + x = \lim_{u \to \infty} \sqrt{u^2 - 2u} - u =$ $\lim_{u \to \infty} \frac{(\sqrt{u^2 - 2u} - u) \cdot (\sqrt{u^2 - 2u} + u)}{\sqrt{u^2 - 2u} + u} = \lim_{u \to \infty} \frac{-2u}{\sqrt{u^2 - 2u} + u} =$ Now, let's divide numerator and denominator by u $= \lim_{u \to \infty} \frac{-2}{\sqrt{1 - \frac{2}{u}} + 1} = -1$

One way to solve the problem: make the substitution, $u = -x$ . Then the problem becomes $\displaystyle{ \lim_{u \rightarrow +\infty} \sqrt{u^2 - 2u} - u }$

$= \lim_{u \rightarrow \infty} u(\sqrt{1 - \frac{2}{u}} - 1)$

$\displaystyle{ = \lim_{u \rightarrow \infty} \frac{\sqrt{1 - \frac{2}{u}} - 1}{\frac{1}{u}} }$

$= \lim_{t\rightarrow 0} \frac{\sqrt{1 - 2t} - 1}{t}\quad (t = 1/u)$

$= \lim_{t \rightarrow 0} \frac{-2}{2\sqrt{1 - 2t}} \quad (\text{L'Hopital's Rule})$

$= -1$

Note: it is much easier to solve the problem if we notice at step 1 that $\lim_{u \rightarrow +\infty} \sqrt{u^2 - 2u} - u = \lim_{u \rightarrow +\infty} \sqrt{u^2 - 2u + 1} - u$ since $u$ goes to infinity. But this intuitively clear step requires some justification.

I cheat on these. Simply substitute a fairly large -x. Here -10 is big enough, yielding (80)^1/2-10~9-10=-1.

When $x$ is negative then $x = -\sqrt {x^2}$ . Rationalizing the numerator, one gets $\dfrac{2x}{\sqrt{x^2+2x} - x}$ . Dividing the top and bottom both by $x$ means dividing the bottom by $-\sqrt{x^2}$ . One gets $\dfrac 2 {-\sqrt{1+\frac 2 x} - 1}$ , so the limit is $-1$ .

you could go the long way and go $\lim_{x \to -\infty} (f(x+\delta_{x})-f(x))/\delta_{x }$ and work your way through it, perhaps do a Taylor expansion, but you'll find that a couple of substitutions, say x=-10 and x=-100 shows this sequences quickly converges to $-1\ as\ x\ \to -\infty$

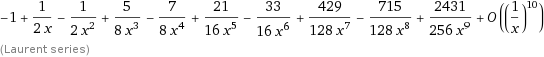
mana yang dari Indonesia....