A circle between two squares

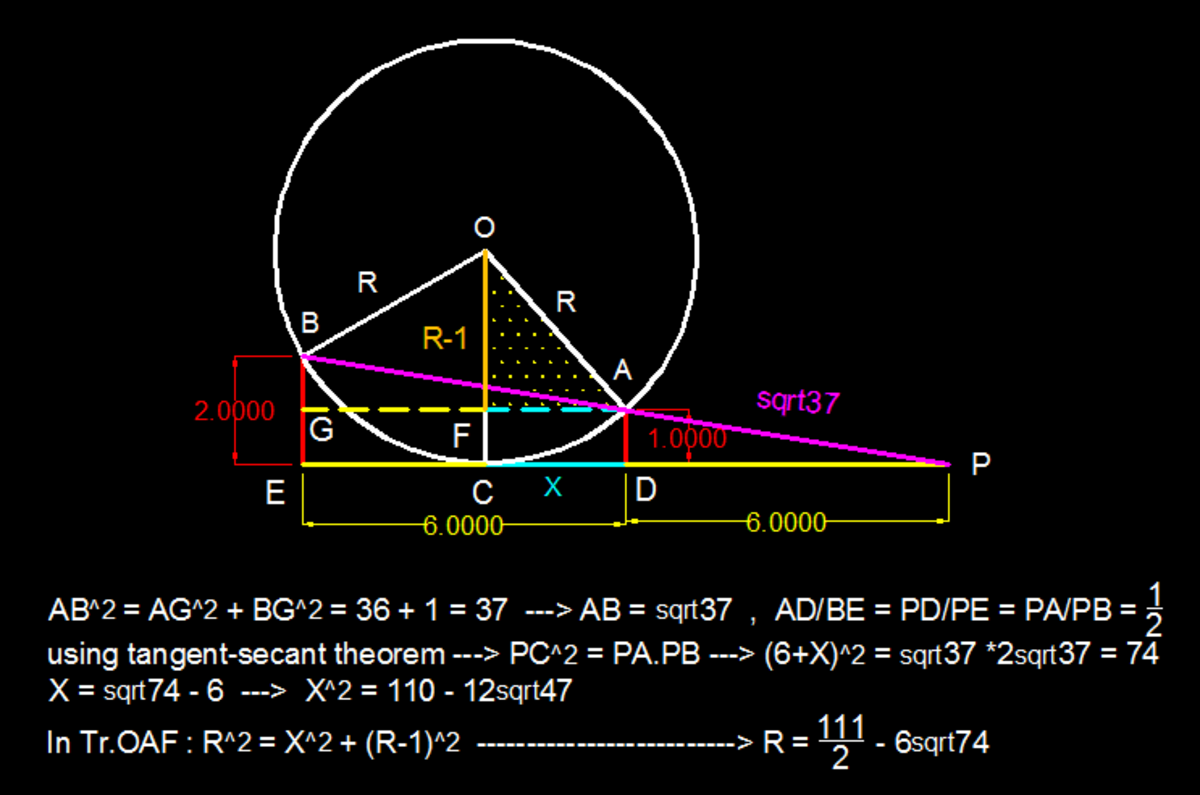
Let the radius of the circle be $r$ . Then, using Pythagorean theorem , we have:

$\begin{aligned} \sqrt{r^2-(r-1)^2} + \sqrt{r^2-(r-2)^2} & = 6 \\ \sqrt{r^2-(r^2-2r+1)} + \sqrt{r^2-(r^2-4r+4)} & = 6 \\ \sqrt{2r-1} + \sqrt{4r-4} & = 6 & \small \color{#3D99F6} \text{Squaring both sides} \\ 2r - 1 + 2\sqrt{(2r-1)(4r-4)} + 4r-4 & = 36 \\ 2\sqrt{8r^2-12r+4} & = 41 - 6r & \small \color{#3D99F6} \text{Squaring both sides} \\ 32r^2-48r+16 & = 36r^2 - 492r + 1681 \\ 4r^2 -444r +1665 & = 0 \end{aligned}$

$\begin{aligned} \implies r & = \frac {444-\sqrt{444^2-4(4)(1665)}}8 & \small \color{#3D99F6} \text{Note that } \frac {444 \ {\color{#D61F06}+}\sqrt{444^2-4(4)(1665)}}8 > 6 \text{, rejected} \\ & = \frac {444 - (4)(3)\sqrt{37^2-185}}8 \\ & = \frac {111 - 3\sqrt{1184}}2 \\ & = \frac {111}2 - 6\sqrt{74} \end{aligned}$

$\implies a+b+c+d = 111+2+6+74 = \boxed{193}$ .

If x is the radius of the circle then, we need to solve the equation sqrt(x^2 - (x-2)^2) + sqrt(x^2 - (x-1)^2 ) = 6

Solving this yields x = 111/2 - 6sqrt(74)