JEE Advanced Mechanics Problem

Classical Mechanics Level 5

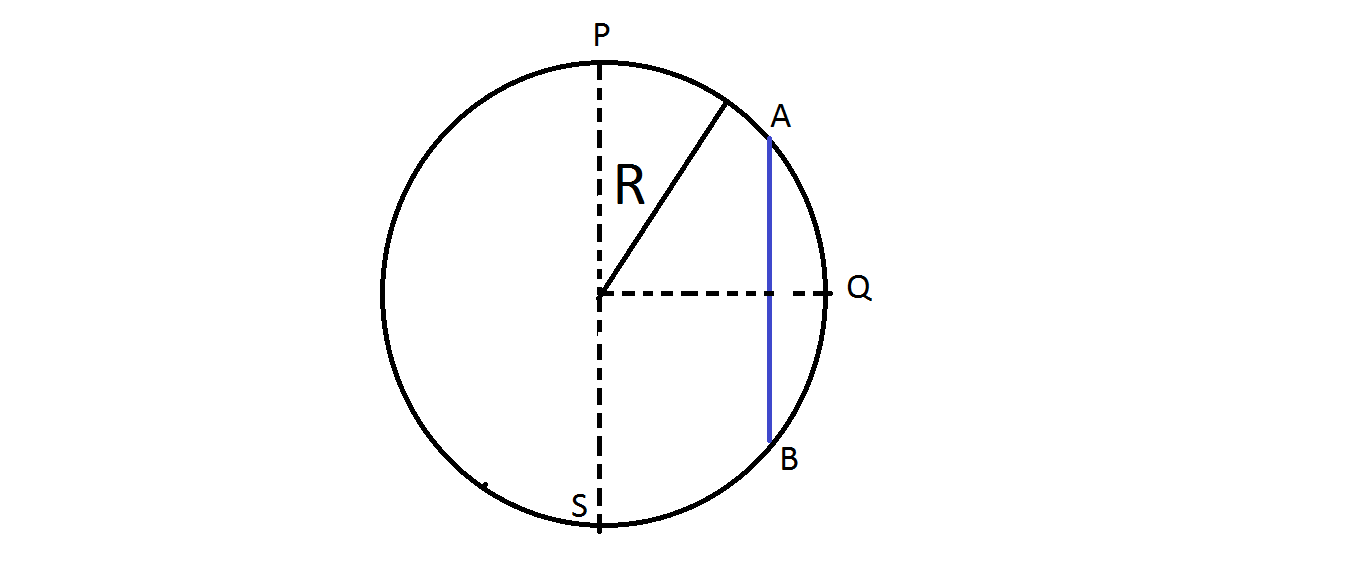
In the above diagram, a rod $AB$ of mass $m$ and length $L$ is held such that the length of the rod is symmetric in semi-circle (massless) $PQS$ about $P$ . Now, the rod is left.

Find the velocity of end $B$ when the center of rod reaches $S$ .

Round your answer to the nearest integer

Details and Assumptions :

Radius of fixed vertical circle (frictionless), $R = 10\text{ m}$ .
Length of rod, $L = 2\sqrt{19} \text{ m}$ .
$g = 10\text{ m/s}^2$

The answer is 15.

1 solution

Vedant Jadhav
May 5, 2018

Here we assume that there is no friction between the rod and the circle and the rod is always in contact with the circle. Now, we can see that on the COM only one force is acting that is the weight of the rod. So the COM of rod performs circular motion around the centre of the circle. Radius of circular motion is given by $r = \sqrt{R^2-l^2/4} = 9.$ Now the velocity of COM when it reaches the axis on which point S lies, its velocity is given by energy conservation. $\frac{1}{2}mv_c^2 = mgr$ $=>$ $v_c = \sqrt{2gr}.$ Substituting the values we get $v_c = 3\sqrt{20}.$ Now the rod is a rigid body and the angular velocity of the COM of the rod is the angular velocity of all the points on the rod. Therefore, $w_c = \frac{v_c }{r} => w_c = \frac{\sqrt{20}}{3}.$ Now let's take velocity at point B as $v_1$ when the centre of rod reaches point S . Therefore as stated above $w$ is same for all points on the rod. Therefore $w_c = w_B$ . The velocity at B is tangential to the circumference and the radius of circular motion is equal to $R = Radius of Circle = 10.$ Therefore $w_B = \frac{v_1}{R}.$ Which implies that $w_c = \frac{v_1}{R}.$ On substituting the values we get $v_1 = \frac{10\sqrt{20}}{3} = 14.907$ Rounding up to the nearest integer, $v_1 = 15ms^{-1}.$

@Vedant Jadhav , The instantaneous axis of rotation of rod is the center of circle. By energy conservation between Q and S, mgR=1/2(I)(w^2). here (w is angular velocity of rod when its center reaches at S) and I is the moment of inertia of rod about the center of Circle perpendicular to the plane of circle, which yields velocity of B as 18.13 m/s. Where am i wrong?

Priyanshu Mishra - 2 years, 3 months ago

Here, as you have considered, the instantaneous axis of rotation of the rod will always be the centre of the rod. So the moment of inertia I will be (ml^2)/12 + mr^2. After calculating, we get this equal m x 262/3. Also, the potential energy is conserved with respect to IAOR. So mgR = (1/2) x I x (w^2). So on substituting the values, we get, w = 1.513 rad/s. Now vB is w x R. So, vB = 1.513 x 10. So we get vB approximately 15m/s.

Vedant Jadhav - 2 years, 3 months ago

I am confused. Shouldn't change in potential energy be mg*sqrt(R^2-l^2/4)?

Jacob Sony - 1 year, 11 months ago

@Jacob Sony – Man the center reaches at S, the distance of S and center of circle is R. so $\delta U = mgR$

Priyanshu Mishra - 1 year, 11 months ago

@Vedant Jadhav you have applied energy conservation wrongly. The total kinetic energy of the rod is $K=\dfrac{1}{2} mv^2+\dfrac{1}{2} \dfrac{ml^2}{12} \omega^2$ The loss in potential energy is $-\Delta U=mgr; ~~~r=9 \text{ meter}$ Further using contact constraint b/w rod and sphere gives $v=9 \omega$ .

Solving $K+\Delta U=0$ yields $\omega = \sqrt{\dfrac{270}{131}}$ which means that $V_B=\sqrt{v^2+19\omega^2}=14.35 \text{m/s}$ .

The correct answer is 14. @Steven Chase