An Application of Archimedes' Principle
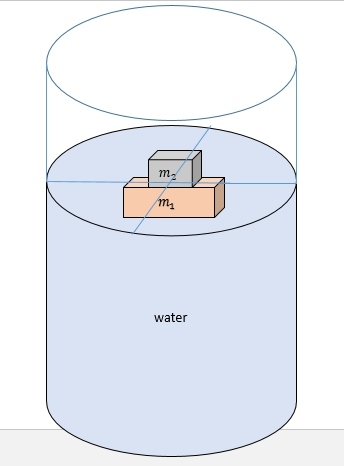
A block m 1 with density ρ 1 floats in a cylindrical bucket of water of cross-sectional area A, with a block m 2 of density ρ 2 on top. Assume that block m 1 is just barely submerged so that the water line is at the bottom of m 2 . Let ρ 0 be the density of water and assume that ρ 0 < ρ 2 .
Now, block m 2 is removed from the top of m 1 and placed on the bottom of the bucket.
Given that ρ 1 = 3 ρ 0 , and that the volume V 1 of m 1 is twice the volume V 2 of m 2 , find the value of K such that Δ H = K A V 2 , where Δ H denotes the change in the height of the water: Δ H = ( final height ) − ( initial height ) .
The answer is -3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
I think discussion of the force N is a red herring. Water is incompressible. The change in height is merely a function of the submerged volume of m1 and m2. In the initial configuration, all of m1 is submerged and none of m2 is submerged. It is given that the density of m1 is 1/3 the density of water. Therefore, when m2 is removed, only 1/3 of m1 will be submerged. Although this tells us that m2 is 2/3 the weight of m1, the information is irrelevant. So, the final total volume submerged is V2 + 1/3 V1. Since the problem is expressed in terms of V2, and V1 = 2 V2, the total submerged volume becomes V2 + 2/3 V2 = 5/3 V2. The difference in height is just the difference in submerged volume divided by the area, A, dH = (5/3 V2 - 2 V2)/A = -1/3 V2/A = V2/KA. Therefore, K = -3.
Log in to reply
You are right that the answer can be found without explicit mention of the buoyant force or its change (It changes by the amount of support of the system other than the buoyant effect of the water, i.e., the normal force on m2.). However the title of the of the problem is An Application of Archimedes' Principle. I view the problem as pedagogical. Since Archimedes' Principle involves the buoyant force in its statement, my solution is intended to make explicit use of the change in the buoyant force, which turns out to be the normal force on m2, as expected intuitively. Therefore, I would not call the discussion of N a red herring. Rather, it is a way of conceptualizing the problem.
I would like to add that your solution is conceptually the same as that of Dhanvanth Balakrishnan below, but without the detail that he provided; specifically the explicit use of Archimedes' Principle to get the submerged portion of m1 in the final configuration.
Log in to reply
I called it a red herring because you define N as the force exerted by the bottom of the bucket on m2. Since m2 is heavier than m1, and is neither connected to it, nor floating underneath it, what is the relevance of N? Since you arrive at the correct answer, I assume there is numerical equality, but I don't see any reason for it. As to the solution below, I still take exception to the assertion "weight of water displaced in the second case is due to both m1 & m2" as it applies to Archimedes Principle. The volume of water displaced does depend on both m1 and m2, but the buoyant force is only relevant to m1, and is independent of m2.
Log in to reply
@Tom Capizzi – I consider m1 and m2 as a system and the buoyant force I refer to is the net buoyant force on the system. There is still a buoyant force acting on m2, even though it rests on the bottom of the bucket (This is the reason that a stone submerged in water seems to weigh less than when lying on the beach.). It is the sum of the buoyant force on m2 and the normal force on m2 that supports m2.
If there were two floating masses (not connected) you would agree that the sum of the buoyant forces on the two would equal the sum of weights of water displaced by the two floating masses, would you not? Archimedes Principle applies to objects whether floating, partially submerged, or fully submerged.
https://en.wikipedia.org/wiki/Archimedes'_principle
Log in to reply
@Dale Gray – Ahh. The Principle applies, but the buoyant force on m2 has nothing to do with the height of the water, given that it's less than the weight of m2.
Log in to reply
@Tom Capizzi – The buoyant force on m2 equals the weight of the water displaced by m2 and therefore contributes to the volume of water displaced by both masses and thus the height of the water column. What I think you are missing is that the totality of weight of the system in the final configuration is supported by the total buoyant force plus the force of support of the bottom of the bucket on m2. In the initial configuration the entire weight of the two masses is supported by the buoyant force, but in the final configuration the total weight is partially supported by the bottom of the bucket. That force is called the normal force N.
When m 2 is placed over m 1 , m 1 is submerged completely.So the amount of water displaced is equal to the buoyant force acting on m 1 .Let the rise in the level of water be h 1 in this case.
v 1 =volume of m 1
v 2 =volume of m 2
A =area of the cross section of the bucket
Weight of water displaced = ρ 0 v 1 g
ρ 0 A h 1 g = ρ 0 v 1 g
A h 1 = v 1
Now, after we remove m 2 and place it at the bottom of the bucket, m 1 will rise by a certain amount until its weight is balanced by the buoyant force acting on it.Let v 3 be the volume of m 1 immersed.
So,
m 1 g = v 3 ρ 0 g
v 1 ρ 1 = v 3 ρ 0
v 3 = 3 v 1
So,weight of water displaced in the second case is due to both m 1 & m 2 .Let the rise in the level of water be h 2 in this case.
Weight of water displaced = ρ 0 g ( 3 v 1 + v 2 )
ρ 0 A h 2 g = ρ 0 g ( 3 v 1 + v 2 )
A h 2 = 3 v 1 + v 2
A h 2 = 3 2 v 2 + v 2
A h 2 = 3 5 v 2
Therefore change in height is,
Δ H = h 2 − h 1
A Δ H = 3 5 v 2 − v 1
A Δ H = 3 5 v 2 − 2 v 2
Δ H = 3 A − v 2
On comparing Δ H = K A v 2
K = − 3
Thanks for the correction.
Good solution, but there is a typo in the sixth equation from the bottom. There should be a factor of A in each term on the right so that you can make the substitutions for Ah1 and Ah2 in terms of v1 and v2.
We know that the change in volume , A . Δ H is given by :
A . Δ H = V 2 − V 1 ′ ′ (1),
with V 2 given and V 1 ′ ′ the part of block 1 that comes above water after removing block 2.
Now because of equilibrium, the force of buoyancy is just as large as the force of gravity on block 1, after we have removed block 2. This gives us :
ρ 0 . V 1 ′ . g = m 1 . g or ρ 0 . V 1 ′ = ρ 1 . V 1 and V 1 ′ = 3 V 1 ,
with V 1 ′ the volume under water after removing block 2.
Now V 1 ′ ′ = V 1 − V 1 ′ = 3 2 V 1 = 3 4 V 2 .
Plugging this into (1), we get A . Δ H = V 2 − 3 4 V 2 = − 3 V 2 , and K = -3.
Let the volume of water in the tube before anything is added be V w . Then notice that when the initial combination of blocks is added, one on top of the other, the volume of water displaced is clearly equal to V 1 . The total volume of the cylinder formed by the water and anything submerged in it is going to be
V w + V 1
By the volume of a cylinder, this makes the original height
H 1 = A V w + V 1
Next, consider the second state of affairs. Since ρ 2 > ρ 0 , we know that the block m 2 will sit at the bottom of the tube and hence displace a volume of water equal to V 2 . Additionally the block m 1 will sit at the surface of the water, partially submerged. Since the weight of water it displaces is equal to the weight of the block, paraphrasing Archimedes' Principle where the object is in equilibrium, we can say that (letting V D 1 represent the volume displaced by block m 1 in this second case)
m 1 g = ρ 0 V D 1 g
V D 1 = ρ 0 m 1
Using the substitution that ρ 0 = 3 ρ 1
V D 1 = 3 ρ 1 m 1
Since, in general, V = ρ m
V D 1 = 3 V 1
The total volume of the new cylinder of water and anything submerged in it is going to be
V W + V 2 + V D 1 = V W + V 2 + 3 V 1
The new height is therefore
H 2 = A V W + V 2 + 3 V 1
And the change in height
Δ H = H 2 − H 1 = A V W + V 2 + 3 V 1 − A V w + V 1 = A V 2 + 3 V 1 − V 1 = A V 2 − 3 2 V 1
Using the substitution that V 1 = 2 V 2
Δ H = A V 2 − 3 4 V 2 = − 3 A V 2
Thus we conclude that K = − 3
Initially the buoyant force B supports both blocks, but after m₂ is placed on the bottom of the bucket, the buoyant force on the system of blocks is less than the sum of the weights of the blocks. This is so because m₂ is now partially supported by the normal force N exerted on it by the bottom of the bucket. The buoyant force is therefore decreased and the change is
Δ B = m 1 g + ( m 2 g − N ) − ( m 1 g + m 2 g ) = − N ,
where g is the acceleration of gravity. The normal force N is the difference in the weight of m₂ and the buoyant force exerted by the water on m 2 . By Archimedes' principle that buoyant force is ρ 0 V 2 g , so
N = = = m 2 g − ρ 0 V 2 g ρ 2 g V 2 − ρ 0 V 2 g ( ρ 2 − ρ 0 ) g V 2 .
Using Archimedes' principle again, with the fact that m 1 is initially fully submerged, as stated in the problem, one can determine ρ 2 in terms of ρ 0 .
ρ 1 V 1 g + ρ 2 g V 2 = ρ 0 g V 1 .
Remembering that V 1 = 2 V 2 and solving for ρ 2 , one finds
ρ 2 = 2 ( ρ 0 − ρ 1 ) .
It is given in the statement of the problem that ρ 1 = ρ 0 / 3 . Therefore, ρ 2 = 4 ρ 0 / 3 . Substituting above gives
N = 3 1 ρ 0 g V 2 . Thus, Δ B = − 3 1 ρ 0 g V 2 .
By Archimedes' principle Δ B = ρ 0 g Δ V , where Δ V is the change in the volume of displaced water. Using Δ V = A Δ H in the preceding equations gives
Δ H = − 3 A V 2 .
By comparing with the form
Δ H = K A V 2
given in the statement of the problem, one finds K = − 3 .