Pulleys+Impusle+Acceleartion!
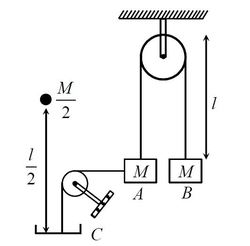 Two blocks
A
and
B
of same mass
M
are connected with each other with an ideal string of length
2
l
passing over an ideal pulley. The block
A
is connected to a light pan
C
with an ideal string as shown in figure. A particle of mass
2
M
is dropped on pan from height
2
l
as shown. If collision between particle and pan is plastic, acceleration of
B
just after the collision is?
Two blocks
A
and
B
of same mass
M
are connected with each other with an ideal string of length
2
l
passing over an ideal pulley. The block
A
is connected to a light pan
C
with an ideal string as shown in figure. A particle of mass
2
M
is dropped on pan from height
2
l
as shown. If collision between particle and pan is plastic, acceleration of
B
just after the collision is?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
At last you equated v 2 / l = a . I have a confusion about that.
The velocity acquired by block A is due to impulsive tension. And impulse in just a large force which acts for small period of time. right? Then how can we write v 2 / l = a . I mean this doesn't seem to be a circular motion. Please help. :)
Log in to reply
Correct me if i am wrong In circular motion, it is said that the centripetal force acts only for a very very short period of time, hence is able to only change the direction but not magnitude of the velocity.
Similarly in a collision, the impulsive-collision forces act for a very short period of time, but they are able to change the direction as well as magnitude of velocity, considering an inelastic collision. The collision lasts for a very short period of time, almost instantaneous.
*Why is that Why is collision force able to change magnitude when it acts for a short period of time as well?
The reasoning that collision forces have a very high magnitude won't work here, as say they have a magnitude 100,000 N, then imagine the circular motion to be of a mass 1 k g and speed 1 0 0 , 0 0 0 m / s and radius 1 m , now we have both centripetal and collision forces equal but still centripetal force is able to only change direction.
Similarly we can always adjust both the forces and circle's radii accordingly, so that impulse provided by both the forces, centripetal and collision forces are always equal.
Log in to reply
This question came in one mock test of JEE Advanced, & the solution i have posted is what they have provided
Log in to reply
@Nishant Rai – At that very moment, when the collision occurs, there is a sudden impulsive force which acts on the block A , ( for a very short duration of time), which i think can be considered as the centripetal force. (I am not talking about the motion afterwards, but at that instant only.) And since the blocks are connected with a string, B also has the same acceleration at that moment.
Log in to reply
@Nishant Rai – Thanks for replying. :)
The impulse on the block A is towards leftwards and it is acting in direction of the velocity of the block A just after the collision. If that has to be equated to centripetal force then that should be acting perpendicular to the tangential velocity. Sorry, if I am missing some thing very obvious.
Log in to reply
@Satvik Pandey – Call the horizontal displacement of block A x (therefore x ˙ is the horizontal velocity and x ¨ is the horizontal acceleration of block A).
If you assume the motion of block A after the collision is purely horizontal (which is true only if the collision lasts a negligible amount of time) then you can find the following equation for block B's acceleration (from conservation of string-length)
a B = l 2 + x 2 x ˙ 2 + x x ¨ − ( l 2 + x 2 ) 3 / 2 ( x x ˙ ) 2
Now we said the collision lasts a negligible amount of time, therefore x = 0 and so the equation reduces to a B = l x ˙ 2
So you can get this answer without even considering any circular motion.
Log in to reply
@Nathanael Case – Nice explanation bro!! :) I got it! Thank you!
Good to see you back on brilliant. :)
Log in to reply
@Satvik Pandey – Thank you Satvik, I'm glad to be back, and I'm glad there are new problems being posted so I can continue to learn :)
how do you draw the pulley diagram? Is there any website?
Call the horizontal displacement of block A x (therefore x ˙ is the horizontal velocity and x ¨ is the horizontal acceleration of block A).
First we should relate the acceleration of B with the motion of A. If you assume the vertical acceleration/motion of block A is zero, then you can find the following relationship in multiple ways, so I leave the derivation to the reader.
a B = l 2 + x 2 x ˙ 2 + x x ¨ − ( l 2 + x 2 ) 3 / 2 ( x x ˙ ) 2
Again, this is assuming the vertical acceleration of block A is zero, which in turn assumes the collision time is negligible (which we have to assume in order to get an answer).
The speed of the pan/particle after the collision ( V f ) must equal the speed of block A (because we have to assume the string is inextensible).
If the tension is T and the collision time is Δ t then the change in momentum is T Δ t therefore:
V f = m p a r t i c l e + m p a n m p a r t i c l e 2 g h − T Δ t = x ˙ = m A T Δ t
m p a n = 0 so we will just say m p a r t i c l e ≡ m p and so now we can rearrange the previous equation into V f = x ˙ = m p + m A m p 2 g h
Now, we assumed Δ t was a negligible amount of time, which implies that x = 0 , which means that our original equation for a B reduces to a B = l x ˙ 2
We already know x ˙ so now we can finish the problem with just algebra and we get a B = l ( m p + m A ) 2 2 g h m p 2 then use the conditions m p = 0 . 5 m A and h = 0 . 5 l and you will get a B = 9 g
Nice solution! +1