Heat Capacity + Vaccum + Springs +Heat!
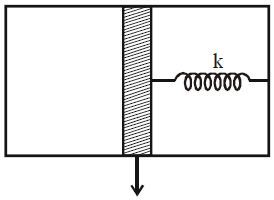 The figure shows a system with adiabatic walls, a piston and a spring. The space on the left side of the piston is filled with 1 mole of an ideal mono atomic gas and right side is a vacuum with a spring. Initially the system is in equilibrium. Now the gas is heated. Molar heat capacity of the gas in this case is
C
=
2
n
R
. What is the value of
n
is?
The figure shows a system with adiabatic walls, a piston and a spring. The space on the left side of the piston is filled with 1 mole of an ideal mono atomic gas and right side is a vacuum with a spring. Initially the system is in equilibrium. Now the gas is heated. Molar heat capacity of the gas in this case is
C
=
2
n
R
. What is the value of
n
is?
(Neglect heat capacities of wall, piston & spring)
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
This problem is not correct. Who told you that A x = V ?
Log in to reply
k x = 0 when P = 0 i.e no gas is injected . Hence x is related to volume as A x = V .
Log in to reply
Volume of the gas is A l where l is the length on the left hand side of piston. Agreed? Now how is l = x ? It is not mentioned that the spring is as long as the container.
Log in to reply
@Raghav Vaidyanathan – If we balance forces then force by gas=PA (Initial state)(Left hand side)
Then on the right hand side we have no force as spring is in uncompressed state.
Hence forces are not balanced.
Thus we are left with 1 case.(which is that the pressure due to gas=0)
Do reply.
Log in to reply
@Mahimn Bhatt – Nope, pressure due to gas is not zero. It is given that the spring is initially in compressed state and the system is in equilibrium.
Log in to reply
@Raghav Vaidyanathan – ohk got it
Log in to reply
@Mahimn Bhatt – But basically we need to find out the relation between P and V. That way thinking makes it more easier to solve. Isnt it?
@Raghav Vaidyanathan – Yep thats an error.
In fact this is the third time this problem is posted on brilliant.
Since Piston is masless , hence Forces are balanced on each side of it .
P g A ∝ K x P g A 2 ∝ K A x P g A 2 ∝ K V P g V − 1 = λ ⇒ x = − 1 C = C v + 1 − x R C = 2 4 R